
- •1 Основное кинетическое уравнение массопередачи. Коэффициент массопередачи и движущая сила процесса.
- •2 Движущая сила массообменного процесса при нелинейной равновесной зависимости. Число единиц переноса и его физический смысл.
- •3.Выражение для средней движущей силы и числа единиц переноса при линейной равновесной зависимости.
- •4.Модифицированные уравнения массопередачи. Число единиц переноса. Высота эквивалентная единице переноса.
- •6.Массобмен в системах без твердой фазы . Молекулярная и конвективная диффузия.
- •8.Молекулярная диффузия. Первый закон Фика. Коэффициент диффузии и его физический смысл.
- •9.Уравнение Щукарева. Коэффициент масоотдачи и его физический смысл, сопоставление с коэф. Массопередачи.
- •10.Выражение коэф массопередачи через коэф массоотдачи.
- •11.Равновесие в системах газ-жидкость. Закон Генри. Ур-е равновесной зависимости. Влияние давления и температуры на абсорбцию.
- •12.Равновесие в процессах пар-ж для идеальных смесей. Закон Рауля. Диаграммы t-X-y и X-y.
- •13. Принципиальная схема противоточной абсорбции и графическое изображение процесса.
- •14. Принципиальная схема абсорбции с рециркуляцией жидкости и графическое изображение процесса.
- •15. Схема ректификационной установки непрерывного действия. Материальный баланс ректификационной колонны. Флегмовое число.
- •16. Уравнения рабочих линий процесса ректификации для непрерывно действующей ректификационной колонны. Минимальное и оптимальное флегмовое число.
- •18. Влияние флегмового числа на размеры ректификационной колонны и расход тепла при ректификации. Оптимальное флегмовое число.
- •20. Схема периодически действующей ректификационной установки. Изображение процесса в у-х диаграмме при постоянном составе дистиллята.
- •22Построение кинетической кривой и определение числа тарелок.
- •23. Порядок расчета ректификационной тарельчатой колонны.
- •24.Гидравлический расчет тарельчатых абсорбционных(ректификационных)колонн.
- •21. Тепловой баланс процесса ректификации
- •27.Непрерывная противоточная экстракция .Материальный баланс.Графическое изображение процесса.
- •28.Ступенчатая противоточная экстракция .Принципиальная схема .Графическое изображение процесса.
- •29. Многократная экстракция с противотоком растворителя.
- •30. Массопередача в системах с твёрдой фазой.Массопроводность.Диф-ные ур-ния массопров-ти.
- •31. Процесс сушки. Технические способы проведения процесса. Виды связи влаги с материалом.
- •32. Основные способы сушки. Материальный баланс конвективной сушки.
- •33 Диаграмма состояния влажного воздуха (Диаграмма Рамзина)
- •34 Изображение в диаграмме н-х процессов изменения параметров влажного воздуха. Температура точки росы, охлаждение, нагревание, смешивание.
- •35 Уравнение рабочей линии сушки. Построение рабочей линии в н-х диаграмме.
- •36 Тепловой баланс воздушной сушки. Уравнение рабочей линии процесса сушки.
- •37.Параметры, влияющие на процесс сушки. Способы интенсификации сушка.
- •38.Сушка с многократным промежуточным подогревом воздуха. Схема и н-х диаграмма.
- •39.Сушка с частичным возвратом отработанного воздуха.Схема и н-х диаграмма.
- •40.Сушка с замкнутой циркуляцией высушиваемого газа. Схема и н-х диаграмма.
- •41. Процесс адсорбции. Динамическая и статическая активности адсорбентов. Условия, влияющие на
- •42. Физическая сущность процесса адсорбции. Адсорбенты. Условия, способствующие протеканию процесса адсорбции.
- •43. Ионообменные процессы – основные закономерности,
- •44. Кристаллизация. Основные способы проведения кристаллизация. Равновесие в процессах кристаллизации.
- •45. Мембранные процессы. Классификация мембранных процессов в зависимости от их механизма. Область применения.
- •46. Влияние различных параметров на селективность и проницаемость мембран
- •47. Материальный и тепловой баланс изогидрической кристаллизации
- •48. Материальный и тепловой баланс кристаллизации с удалением части растворителя.
6.Массобмен в системах без твердой фазы . Молекулярная и конвективная диффузия.
В процессах переноса распределяемого вещества (массы) из одной фазы в другую надлежит различать два случая: 1) перенос из потока жидкости в поток жидкости, или массообмен между потоками жидкости, и 2) перенос из твердого тола в поток жидкости (или перенос в обратном направлении), т. е. массообмен между твердой фазой, содержащей внутри пор или капилляров распределяемое вещество, и потоком жидкости.Элементарными законами, которым подчиняется перенос распределяемого вещества из одной фазы в другую, являются закон молекулярной диффузии, закон массоотдачи и закон массопроводности.
Закон молекулярной диффузии или 1ый закон Фика.
Молекулярная диффузия в газах или р-ах жид-ти происходит в результате хаотического движения молекул. Перенос ве-ва осуществляется из области с более высокой концентрации в обл-ть с более низкой концентрацией, независимо от движения потоков.
В этом случае кинетика пр-са подчин. 1му закону Фика: кол-во продифундировавшего ве-ва пропорционально пл-ди перпендикулярной напряж. Диффузионного потока и временем,т.е.
dM=-D*![]() (dM-кол-во
продифунд.ве-ва;D-коэф.диффузии,
(dM-кол-во
продифунд.ве-ва;D-коэф.диффузии,![]()
D-показывает какое кол-во ве-ва дифундирует через пов-ть в 1м2 в течении 1сек. При разности концентраций на расстоянии 1м=1
Размерность D зависит от 1,от агрегатного состояния сис-мы,2. С увелеичением температ.коэф. диффузии увеличивается.3 с увелич.давления коэф.дифуз.уменьшается.
2.Ковективная диффузия.
В основу рассмотрения явления конвективной диффузии положена теория диффузионного граничного слоя, которую разделяют большинство ученых Советского Союза.

Рис. 11-10. К формулировке закона конвективной диффузии.
Согласно этой теории (рис. 11-10), распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непосредственно потоками жидкости и молекулярной диффузией. При этом воспринимаю- Гг( щая распределяемое вещество фаза считается либо твердой, либо близкой к ней (по способности гасить турбулентные пульсации потока). В рассматриваемой системе поток можно считать состоящим из двух частей: ядра и граничного диффузионного слоя. В ядре перенос вещества осуществляется преимущественно токами жидкости и в условиях достаточной турбулентности течения; концентрация распределяемого вещества в данном сечении и в условиях стационарного режима сохраняется постоянной. По мере приближения к граничному диффузионному слою турбулентность и, следовательно, турбулентный перенос затухают, с приближением к границе начинает превалировать перенос за счет молекулярной диффузии. Соответственно этому появляется градиент концентрации распределяемого вещества, растущий по мере приближения к границе. Таким образом, область граничного диффузионного слоя — это область появления и роста градиента концентрации, область увеличения молекулярной диффузии от пренебрежимо малого значения до максимального.
Если рассмотреть элементарный объем фазы (рис. 11-9), перемещающийся в граничном диффузионном слое, то станет очевидной возможность утверждать, что концентрация распределяемого вещества в нем меняется не только за счет молекулярной диффузии, но также и за счет механического переноса его из одной зоны концентрации в другую. В этом случае концентрация распределяемого вещества будет функцией не только пространственных координат и времени, как в случае только молекулярной диффузии, но и компонентов скорости перемещения элемента.
Соответственно этому изменение анализируемого параметра — концентрации С надлежит выразить через субстанциональную производную
DcC/𝜕𝜏=𝜕c/𝜕𝜏+𝜕C𝜕x*wx+𝜕C/𝜕y*wy+𝜕C/𝜕z*wz
При использовании субстанциональной производной приращение количеств распределяемого вещества в элементе за время 𝜕𝜏 может быть выражено как
dM= DcC/𝜕𝜏*dx*dy*dz
Приращение количества распределяемого вещества за счет молекулярной диффузии определяется равенством (11.44). Приравнивая правые части равенств (11.44) и (11.50), получим уравнение конвективной диффузии:
𝜕C/𝜕𝜏+𝜕C/𝜕x*wx+𝜕C/𝜕y*wy+𝜕C/𝜕z*wz=D(𝜕 2C/𝜕x 2+ 𝜕 2C/𝜕y 2+ +𝜕2C/𝜕xz2)
7.Дифференциальные уравнения молекулярной и конвективной диффузии.
Дифференциальное уравнение молекулярной диффузии (второй закон Фика)
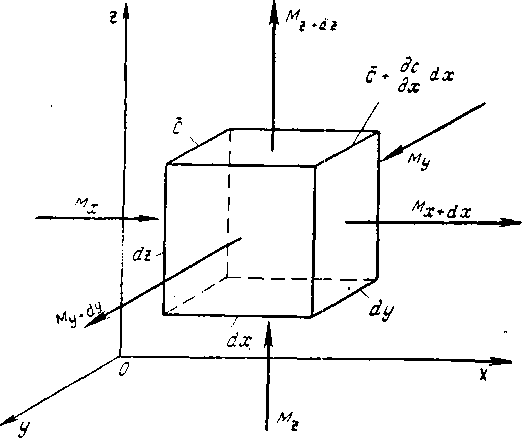
Для вы пода дифференциального уравнения молекулярной диффузии выделим в неподвижной среде или в движущемся ламинарном потоке элементарный параллелепипед с ребрами dх, dу и dz (рис. 11-9).
Если через этот элементарный параллелепипед за счет молекулярной диффузии перемещается распределяемое вещество, то через левую, заднюю и нижнюю грани за время d𝜏 в него входят количества вещества соответственно Мх, Му и Мz, а через противоположные грани — правую, переднюю и верхнюю — выходят количества вещества соответственно Мх+dх, Му+dу и Мг+dz. Следовательно, элемент за время d𝜏 приобретает диффундирующее вещество в количестве
dM = (Мх - Мх+dх) + (МУ- Му+dу) + {Мг – Mz+dz)
При этом концентрация диффундирующего вещества повышается на 𝜕С/𝜕𝜏*d𝜏
Согласно основному закону молекулярной диффузии
Мx=-D*𝜕C/𝜕x*dy*dz*d𝜏
И
Mx+dx=-D*![]() 2C/𝜕x2*dx*dy*dz*d𝜏
2C/𝜕x2*dx*dy*dz*d𝜏
И,следовательно Мx-Mx+dx=D*𝜕2C/ 𝜕x2*dx*dy*dz*d𝜏
Аналогично найдем
Му — Му+dу= D*𝜕2C/ 𝜕x2*dx*dy*dz*d𝜏
Мz— Мz+dz= D*𝜕2C/ 𝜕x2*dx*dy*dz*d𝜏
Складывая левые и правые части трех последних равенств, получим
dM=D(𝜕2C/𝜕x2+𝜕2C/dy2+𝜕2C/ 𝜕z2)*dx*dy*dz* d𝜏
С другой стороны, ту же прибыль количества диффундирующего вещества в элементе можно найти умножением объема элемента на изменение концентрации за время d𝜏, т. е.
dM=dx*dy*dz*𝜕C/𝜕𝜏*d𝜏
Сопоставляя соотношения (11.44) и (11.45), получим дифференциальное уравнение молекулярной диффузии:
𝜕C/𝜕𝜏=D(𝜕2C/𝜕x2+𝜕2C/dy2+𝜕2C/ 𝜕z2)
2.Ковективная диффузия.
В основу рассмотрения явления конвективной диффузии положена теория диффузионного граничного слоя, которую разделяют большинство ученых Советского Союза.

Рис. 11-10. К формулировке закона конвективной диффузии.
Согласно этой теории (рис. 11-10), распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непосредственно потоками жидкости и молекулярной диффузией. При этом воспринимаю- Гг( щая распределяемое вещество фаза считается либо твердой, либо близкой к ней (по способности гасить турбулентные пульсации потока). В рассматриваемой системе поток можно считать состоящим из двух частей: ядра и граничного диффузионного слоя. В ядре перенос вещества осуществляется преимущественно токами жидкости и в условиях достаточной турбулентности течения; концентрация распределяемого вещества в данном сечении и в условиях стационарного режима сохраняется постоянной. По мере приближения к граничному диффузионному слою турбулентность и, следовательно, турбулентный перенос затухают, с приближением к границе начинает превалировать перенос за счет молекулярной диффузии. Соответственно этому появляется градиент концентрации распределяемого вещества, растущий по мере приближения к границе. Таким образом, область граничного диффузионного слоя — это область появления и роста градиента концентрации, область увеличения молекулярной диффузии от пренебрежимо малого значения до максимального.
Если рассмотреть элементарный объем фазы (рис. 11-9), перемещающийся в граничном диффузионном слое, то станет очевидной возможность утверждать, что концентрация распределяемого вещества в нем меняется не только за счет молекулярной диффузии, но также и за счет механического переноса его из одной зоны концентрации в другую. В этом случае концентрация распределяемого вещества будет функцией не только пространственных координат и времени, как в случае только молекулярной диффузии, но и компонентов скорости перемещения элемента.
Соответственно этому изменение анализируемого параметра — концентрации С надлежит выразить через субстанциональную производную
DcC/𝜕𝜏=𝜕c/𝜕𝜏+𝜕C𝜕x*wx+𝜕C/𝜕y*wy+𝜕C/𝜕z*wz
При использовании субстанциональной производной приращение количеств распределяемого вещества в элементе за время 𝜕𝜏 может быть выражено как
dM= DcC/𝜕𝜏*dx*dy*dz
Приращение количества распределяемого вещества за счет молекулярной диффузии определяется равенством (11.44). Приравнивая правые части равенств (11.44) и (11.50), получим уравнение конвективной диффузии:
𝜕C/𝜕𝜏+𝜕C/𝜕x*wx+𝜕C/𝜕y*wy+𝜕C/𝜕z*wz=D(𝜕 2C/𝜕x 2+ 𝜕 2C/𝜕y 2+ +𝜕2C/𝜕xz2)
