ВТОРЫЕ ВОПРОСЫ
Вопрос №1: Основное уравнение массопередачи. Уравнение массоотдачи. Коэффициенты массопередачи и массоотдачи. Их размерности и физический смысл.
Массопередача – сложный массообменный процесс, который включает перенос вещества
•в пределах одной фазы (массоотдача);
•через границу раздела фаз;
•в пределах другой фазы.
Основным кинетическим уравнением массообменных процессов является уравнение массопередачи, которое основано на общих кинетических закономерностях химико-технологических процессов.
Основное уравнение массопередачи, определяющее массу М вещества, переносимого из фазы в фазу в единицу
времени, выражается следующим образом: |
|
|
|
|
М = · · ( − ) (по газовой фазе) |
|
|
М = · · ( − ) (по жидкой фазе), |
где , − равновесные концентрации в данной фазе, соответствующие концентрациям распределяемого вещества в |
||
концентрации фаз Ф (газовая фаза) и Ф (жидкая фаза). |
||
основной массе (ядре) другой |
зы; , |
− коэффициенты массопередачи, выраженные соответственно через |
При такой форме записи уравнения массопередачи движущая сила процесса выражается разностью между рабочей и равновесной концентрацией (или наоборот), отражающей меру отклонения системы от состояния равновесия.
( |
Концентрации фаз изменяются при их движении вдоль поверхности раздела, соответственно изменяется и |
|||
и |
): |
|
|
|
движущая сила массопередачи, поэтому в уравнение массопередачи вводится величина средней движущей силы |
||||
ср |
ср |
|
|
|
|
|
М = |
· · ср |
|
|
|
М = |
|
· · |
|
|
|
ср |
|
|
F – |
поверхность контакта фаз (также обозначается буквой А). |
||
где с – разность концентраций.
Вместо ṅ (мольный расход вещества) может быть использована величина ṁ (массовый расход вещества).
Коэффициент массопередачи ( или ) характеризует скорость процесса переноса вещества из одной фазы в другую; он показывает, какое количество (какая масса) распределяемого вещества переходит из фазы в фазу в единицу времени через единицу поверхности контакта фаз при движущей силе массопередачи, равной единице.
По физическому смыслу коэффициенты массопередачи отличаются от коэффициентов массоотдачи, но выражены
водинаковых с ними единицах измерения.
Взависимости от того, в каких единицах измерения выражается движущая сила процесса массопередачи, коэффициенты массопередачи могут иметь следующие размерности:
•движущая сила представляет собой разность объемных концентраций:
|
|
кг |
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
[м ·сек· кг]=[сек] |
|
|
|
|
|
|||||||
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
• движущая сила представляет собой разность относительных концентраций: |
||||||||||||||
|
|
[ кг |
|
кг]=[ |
|
кг |
] |
|
|
|
|
|||
|
|
м ·сек·кг |
|
м ·сек |
|
|
|
|
|
|||||
• движущая сила представляет собой разность мольных долей: |
||||||||||||||
|
|
|
|
кг |
|
|
|
|
|
|
|
|
|
|
|
[м ·сек·(мольные доли)] |
|
|
|
|
|||||||||
• движущая сила представляет собой разность парциальных давлений (для газовой или паровой фазы): |
||||||||||||||
[ кг |
]=[ |
кг |
Н ]=[ |
|
|
|
|
кг кг·м |
|
]=[сек] |
||||
м ·сек·Па |
м ·сек· |
|
|
м |
|
·сек· |
|
|
|
|
м |
|||
|
|
|
|
|
|
|
|
|
сек |
·м |
|
|||
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
В уравнение массопередачи может |
входить как масса, |
так и количество распределяемого вещества |
||||||||||||
(переносимое в единицу времени в каждой из фаз). Если в уравнение массопередачи входит не масса (килограммы), а количество (киломоли) распределяемого вещества, то во всех приведенных выше единицах измерения килограммы должны быть заменены на киломоли.
Массоотдача – конвективный массообмен между движущейся средой и поверхностью раздела с другой средой
(иначе: перенос вещества от границы раздела фаз внутрь фазы). Скорость массоотдачи пропорциональна движущей силе, |
||
равной разности концентраций в ядре и на границе фазы или (в случае обратного направления переноса) |
– разности |
|
Ф (газовая фаза) |
в фазу Ф (жидкая фаза), то основное уравнение массоотдачи, определяющее количество М вещества, |
|
концентраций на |
границе и в ядре фазы. Если распределяемое вещество переходит |
из фазы |
переносимого в единицу времени в каждой из фаз (к границе фазы или в обратном направлении), можно представить в |
|||
следующем виде: |
|
|
|
М = · · (̅ − ̅гр) (по газовой фазе) М = · · (̅гр − ̅) (по жидкой фазе). |
|
||
процесса массоотдачи соответственно |
в фазах Ф (газовая фаза) и Ф (жидкая фаза), причем ̅ и ̅ |
– средние |
|
Входящие в эти уравнения разности концентр ций ̅ − ̅гр и ̅гр − ̅ |
представляют собой движущую силу |
||
концентрации в основной массе (ядре) |
каждой из фаз, ̅гр и ̅гр – концентрации у границы соответствующей фазы. |
||
|
|
|
|
Коэффициенты пропорциональности |
и называются коэффициентами массоотдачи. |
|
|
В отличие от коэффициента массопередачи, коэффициент массоотдачи характеризует скорость переноса вещества внутри фазы конвекцией и молекулярной диффузией одновременно. Коэффициент массоотдачи является не физической константой, а кинетической характеристикой и зависит от многих факторов:
•физических свойств фазы (плотность, вязкость и т.д.);
•гидродинамических условий в этой фазе (ламинарный или турбулентный режим течения);
•определяющих геометрических размеров и т.д.
Коэффициент массоотдачи показывает, какое количество вещества (какая масса вещества) переходит от единицы поверхности раздела фаз в ядро потока/фазы (или в обратном направлении) в единицу времени при движущей силе, равной единице.
По физическому смыслу коэффициенты массоотдачи отличаются от коэффициентов массопередачи, но выражены в одинаковых с ними единицах измерения (см. подраздел «Коэффициент массопередачи, его размерность и физический смысл»).
Коэффициент массоотдачи может быть выражен в различных единицах в зависимости от выбора единиц измерения для массыкмольраспределяемого· м−2 · сек−1 · (едвещества. движущейдвижущейсилы)−1силы. Для переходакгот·величинм−2 · сек−оэффициентов1 · (ед. движущеймассоотдачисилы)−1, выраженных в , к их значениям в
следует первые умножить на массу 1 кмоль (кг/кмоль) Мк распределяемого компонента.
Зависимость между коэффициентами массопередачи и массоотдачи можно выразить следующим образом:
|
|
|
|
|
|
ɱ |
||
|
|
= |
+ ɱ · |
; |
|
= |
+ |
|
|
|
|
|
|
|
|
||
ВОПРОС №2: Метод кинетической линии рассчёта высоты массообменных аппаратов со ступенчатым контактом фаз. Порядок построения кинетической линии. Эффективность по Мэрфри.
ВОПРОС №3: Что такое теоретическая ступень разделения («теоретическая тарелка»)? Как это понятие применяется для оценки эффективности и расчета массообменных аппаратов со ступенчатым и непрерывным контактом фаз?
Теоретическая ступень разделения («теоретическая тарелка») – соответствуют некоторому гипотетическому участку аппарата, на котором жидкость полностью перемешивается, а концентрация удаляющихся фаз (например, жидкости и газа) являются равновесными.
Общую высоту H аппарата со ступенчатым контактом фаз с помощью числа теоретических ступеней определяют с использованием коэффициента полезного действия колоны η, который равен отношению числа теоретических ступеней к числу необходимых рабочих(действительных) ступеней NДейстит.. Тогда число действительных ступеней определяют из выражения NДейстит. = Nтеор./ η. Определив NДейстит.,рабочую высоту H аппарата со ступенчатым контактом фаз находят: h=( NДейстит. -1) hт; hт – расстояние между ступеньками, которое принимают или рассматривают. Расчет высоты h массообменных аппаратов с непрерывным контактом фаз можно проводить с помощью числа теоретических ступеней по формуле: h = hэкв. Nт.с.; Nт.с. – чисто теоретических ступеней; hэкв. – высота аппарата ( по разделяющему действию) одной ступени изменения концентрации(ВЭТС) или теоретической тарелке(ВЭТТ). ВЭТС и ВЭТТ определяются по эмпирическим зависимостям.
ВОПРОС №4: Диффузионное сопротивление массопереносу. В каких случаях сопротивление массопереносу лимитируется переносом в одной из фаз?
Уравнение массоотдачи показывает, какое количество вещества переносится из ядра потока к границе раздела
фаз или в обратном направлении:
dМ = y ( y − yгр )dF dМ = x (xгр − x)dF
Уравнение массопередачи показывает, какое количество целевого компонента переходит в единицу времени из одной фазы в другую:
dМ = k |
|
* |
)dF |
y |
( y − y |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dМ = k |
(x |
* |
− x)dF |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
y |
гр |
= m.x |
|
|
|
|
|
|
|
|
|
|
|
|
mdМ |
|
|
|
|
|
|
|
* |
|
mdM |
||
|
гр |
|
|
m.( x |
|
− x) = |
|
|
|
|
|
y |
|
|
− y |
= |
|
||||||||||
|
=> |
|
|
|
|
|
|
|
|
|
|
dS |
=> |
|
|
|
|
|
|
|
dS |
||||||
y |
|
= m.x |
|
|
|
|
|
гр |
|
|
|
|
|
|
гр |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
dМ |
1 |
|
|
m |
|
|
|
|
|
|
|
|
|
|
dМ |
|
|
|
|||||
|
|
y − y = |
|
|
|
|
|
|
+ |
|
|
|
но |
|
y |
− y |
= |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
k dF |
|
|
|||||||||||||||
|
|
|
|
dF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
; |
y |
|
− y |
|
= |
dM |
||
гр |
|
dS |
|||
|
|
||||
|
|
|
|||
|
|
|
y |
|
|
|
1 |
|
= |
1 |
+ |
m |
= Ry |
|
|
1 |
|
= |
1 |
+ |
|
|
1 |
|
= R |
|
||||||||
Получим k |
|
|
|
|
|
|
, |
|
k |
|
|
|
|
|
|
|
m |
x |
||||||||||
y |
y |
|
x |
|
|
x |
|
|
|
|
x |
|
|
y |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Если |
|
x очень велик то 1/ y |
>> |
|
m |
тогда |
k y = y |
сопротивление |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
лимитируется в фазе Фy.
Если y |
очень велик то 1/ x >> |
1 |
тогда |
k x = x сопротивление |
|
|
|||||
m y |
|||||
|
|
|
|
лимитируется в фазе Фx.
ВОПРОС №5: Критерии подобия массообменных процессов. Их физический смысл.
|
= |
|
+ |
|
+ |
|
= 2 |
|
Общность дифференциальных уравнений теплообмена |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и массообмена |
|
|
|
|
|
|||
|
= + |
− |
, |
(15.25) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
позволяет полагать, что основные критерии массообменных процессов должны быть аналогичны основным критериям теплообмена.
Рассмотрим уравнения массопереноса на границе раздела фаз. Из одной фазы в другую переходит количество массы,
равное
= F(y – y*гр),
где y*гр равновесная концентрация на границе раздела фаз.
−
Это же количество массы переносится молекулярной диффузией через пограничный слой:
М =
В этих уравнениях трудноопределимы величины y*гр и n-толщина пограничного слоя, через который проходит вещество |
|
y(y - y*гр) = − |
|
молекулярной диффузией. Отсюда |
|
y∆y = − |
|
|
|
или |
|
|
|
где |
|
y - y*гр = ∆y |
|
Перемножим на масштабные множители каждый член последнего уравнения: |
|
α ac ( y∆y) = (ad ac/al )(− ) |
|
|
|
тогда |
|
a al /ad = 1 |
|
l /D = Nu’ |
|
откуда |
|
Где l - определяющий геометрический размер.
Данный безразмерный комплекс является аналогом теплового критерия Нуссельта (Nu = αl/λ,) и называется поэтому диффузионным критерием Нуссельта (иногда — критерием Шервуда Sh). Критерий Нуссельта Nu’
является oпределяемым критерием, поскольку в него входит величина . Так как Nu’ ~ /D, то Nu’ характеризует отношение скорости переноса вещества (конвективного и молекулярного - ) к молекулярному переносу (D).
Другие критерии массообменных процессов получим из дифференциального уравнения конвективной диффузии (15.25).
Переписав уравнение2 (15.25) относительно оси Х:
+ wx = D 2
И проведя его подобное преобразование, получим следующие критерии подобия:
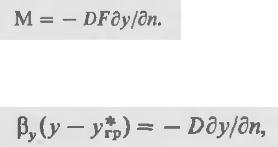
τD/ 2 = Fo’-диффузионный критерий Фурье (аналог теплового критерия Фурье Fo = τα/ 2), который характеризует подобие неустановившихся процессов массообмена;
Wl/D = Ре’-диффузионный критерий Пекле (аналог теплового критерия Пекле Ре = Wl/α). |
|||
Критерий Ре’ ~ W/D характеризует отношение переноса вещества конвекцией (W) к молекулярному переносу (D) в |
|||
′ |
=( ) / ( ) = |
= Pr’ |
|
сходственных точках подобных систем. Часто критерий Ре’ заменяют отношением: |
|||
|
|
|
|
Диффузионный критерий Прандтля Рг’ является аналогом теп-ного критерия Рг = v/а (иногда критерий Рг’ называют критерием Шмидта Sc).
Формально критерий Рг’ выражает постоянство отношения физических свойств жидкости или газа в сходственных точках подобных систем. По существу же критерий Рг’ характеризует отношение профиля скоростей (через v) к профилю концентраций (через D), т. е. отношение толщины гидродинамического и диффузионного пограничных слоев.
Для соблюдения подобия процессов массоотдачи необходимо также соблюдение гидродинамического подобия. Поэтому критериальное уравнение массоотдачи для неустановившегося процесса имеют следующий вид (Г — геометрический симплекс)
Nu’ = f(Fo’, Re, Pr’, Ga, Г1, Г2 ...)
При установившемся процессе и при отсутствии влияния сил тяжести (т. е. при Fo’ = 0 и Ga =0):
Nu’ = f1 (Re, Pr’, Г1, Г2...) |
|
|
|
Например Nu’ = A ( ′) Г Г |
(15.30) |
||
|
1 |
2 |
|
Где A, n, m, q, p определяют опытным путем. |
|
||
Уравнение (15.30) является обобщенным критериальным урав-инем массоотдачи. Поскольку оно аналогично |
|||
критериальному уравнению теплоотдачи (11.35,а), то при одинаковых гидродинамических условиях |
|||
|
= ( ) ^m |
(15.31) |
|
′ |
′ |
|
|
С помощью выражения (15.31) можно найти соотношение между коэффициентами тепло- и массоотдачи: |
|||
= ( )( ) ^m , |
|
||
|
|
|
|
которое позволяет по известному значению, например α, определить величину коэффициента массоотдачи при одних и тех же гидродинамических условиях.
ВОПРОС №6: Массообменный критерий Нуссельта. Каковы его вид и физический смысл?
Рассмотрим уравнения массопереноса на границе раздела фаз:
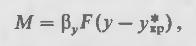где βy –коэффициент массоотдачи, F – поверхность, нормальная к направлению диффузии, y*гр – равновесная концентрация на границе раздела фаз.
Это же количество массы переносится молекулярной диффузией через пограничный слой:
D – коэффициент диффузии.
В этих уравнениях трудноопределимы величины y*гр и n – толщина пограничного слоя, через который проходит вещество молекулярной диффузией. Отсюда
или
где 
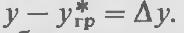
Перемножим на масштабные множители каждый член последнего уравнения:
Данный
безразмерный комплекс является аналогом теплового критерия Нуссельта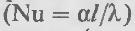 
и называется поэтому диффузионным критерием Нуссельта. Критерий Нуссельта Nu’ является определяемым критерием, поскольку в него входит величина β. Так как Nu’ ~ β/D, то Nu' характеризует отношение скорости переноса вещества (конвективного и молекулярного – β) к молекулярному переносу (D).
ВОПРОС №7: Написать с необходимыми пояснениями и обозначениями выражение для расчёта средней движущей силы массопередачи в аппаратах с непрерывным контактом фаз при условии линейности рабочей и равновесной линий на примере абсорбции. Структура потоков идеального вытеснения.
ВОПРОС №8: Определение минимального и оптимального расхода поглотителя при абсорбции.