Первые вопросы

Вопрос 1 Вывестии дифференциальное уравнение конвективной диффузии. Рассмотреть частный случай диффузии в неподвижной среде.

Рассмотрим перенос массы в неразрывном потоке жидкости при условии постоянства коэффициента молекулярной диффузии D переносимого вещества и отсутствии источников массы (т. е. γ= 0).

Плотность потока массы описывается линейным градиентным уравнением (3.14) первым законом Фика.

_мС= -DgradC (3.14)

В соответствии с основным уравнением переноса количества движения, энергии и массы при учете того, что потенциалом переноса в данном случае является концентрация, получим урав­нение переноса массы

дс/дτ + div c = D div grad с. (3.43)

Проводя преобразования, аналогичные сделанным при выводе уравнения конвективного теплообмена, запишем это уравнение в следующем виде:

дс/дτ + cdiv 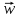+ 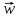grad с = D²c. (3-44)

Поскольку поток неразрывен, div w = 0. Тогда уравнение пе­реноса массы примет вид

дс/дτ + 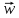grad с = D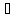²c, (3.45)

или в развернутой форме:

дс/дt + w_xdc/dx + w_ydc/dy + w₂dc/dz = D(д²c/dx² + д²с/8у² + д²c/дz²) = D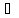²c. (3.46)

Уравнение (3.46) выражает в общем виде распределение кон­центрации компонента в движущемся потоке при неустановившемся процессе переноса массы. Уравнение (3.46) называют также диф­ференциальным уравнением конвективной диффузии.

Для установившегося процесса переноса массы дс/dτ = 0; тогда

w_xдc/дx + w_yдc/дy + w_zдc/дz = D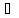²c. (3.47)

Коэффициент молекулярной диффузии D представляет собой физическую константу и характеризует способность данного ве­щества проникать вследствие диффузии в неподвижную среду. Он зависит от природы диффундирующего вещества и среды, темпе­ратуры и давления и не зависит от гидродинамических условий, в которых происходит процесс. Отметим, что коэффициент диффу­зии является аналогом коэффициента температуропроводности а. Таким образом, уравнение (3.46) по структуре аналогично диффе­ренциальному уравнению переноса теплоты (3.40).

В неподвижной среде w_x = w_y = w_z = 0, и уравнение (3.46) обра­щается в дифференциальное уравнение молекулярной диффузии

дс/дτ = D(д² с/дх¹ + д²с/ду² + д²с/дг²), (3.48)

которое носит название второго закона Фика и описывает распре­деление концентраций данного вещества в неподвижной среде.

2. Первый закон Фика. Вывод дифференциального уравнения конвективной диффузии.

Молекулярная диффузия в газах и растворах жидкостей происходит в результате хаотического движения молекул, не связанного с движением потоков жидкости.  В этом случае происходит перенос молекул распределяемого компонента из областей высоких концентраций в область низких концентраций. Кинетика переноса подчиняется в этом случае первому закону Фика, формулировка которого аналогична закону теплопроводности: количество вещества, продиффундировавшего в пределах фазы, пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и времени

– коэффициент пропорциональности, или коэффициент диффузии.

.

Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность 1 м2 в течение 1 с при разности концентраций на расстоянии 1 м, равной единице.

  Знак минус в правой части уравнения показывает, что при молекулярной диффузии направление перемещения вещества и градиент концентраций противоположны друг другу. Размерность коэффициента зависит от способа выражения концентрации распределяемого компонента. Если это объемные концентрации, то размерность коэффициента следующая:

.

Коэффициент диффузии не является постоянной величиной. Это достаточно малая величина для газов. Она на четыре порядка выше, чем для жидкостей. Коэффициент диффузии увеличивается с ростом температуры и уменьшается с повышением давления. Если в газах коэффициент диффузии не зависит от концентрации диффундирующего вещества, то в жидкостях это влияние особенно значимо для неразбавленных растворов.

2)Дифференциальное уравнение массоотдачи (конвективной диффузии).

В основу рассмотрения явления конвективной диффузии положена теория диффузионного пограничного слоя. Согласно этой теории распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непосредственно потоками жидкости и молекулярной диффузией. При наличии конвективной диффузии концентрация распределяемого компонента изменяется не только вследствие молекулярной диффузии, но и механического переноса его из одной области пространства в другую. В этом случае концентрация распределяемого компонента будет функцией не только координат x, y, z и времени , но и составляющих скорости перемещения частиц потока .

При конвективной диффузии бесконечно малый элемент потока перемещается из одной точки пространства в другую. В этом случае изменение концентрации распределяемого компонента может быть выражено субстанциональной производной, которая учитывает изменение ее во времени и изменения, связанные с перемещением элемента из одной  точки пространства в другую:

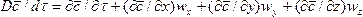.                   (4.21)

В этом равенстве  представляет собой локальное изменение концентрации распределяемого компонента,  а комплекс  – конвективное изменение концентрации.

Если в уравнении молекулярной диффузии (4.17) заменить локальное изменение концентрации  полным , в соответствие с уравнением  (4.21), то можно получить дифференциальное уравнение конвективной диффузии:

  .  (4.22)