ВТОРЫЕ ВОПРОСЫ

Вопрос №1: Основное уравнение массопередачи. Уравнение массоотдачи. Коэффициенты массопередачи и массоотдачи. Их размерности и физический смысл.

Массопередача 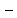сложный массообменный процесс, который включает перенос вещества

• в пределах одной фазы (массоотдача);

• через границу раздела фаз;

• в пределах другой фазы.

Основным кинетическим уравнением массообменных процессов является уравнение массопередачи, которое основано на общих кинетических закономерностях химико-технологических процессов.

Основное уравнение массопередачи, определяющее массу М вещества, переносимого из фазы в фазу в единицу времени, выражается следующим образом:

М = (по газовой фазе)

М = (по жидкой фазе),

где равновесные концентрации в данной фазе, соответствующие концентрациям распределяемого вещества в основной массе (ядре) другой фазы; 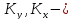коэффициенты массопередачи, выраженные соответственно через концентрации фаз .

При такой форме записи уравнения массопередачи движущая сила процесса выражается разностью между рабочей и равновесной концентрацией (или наоборот), отражающей меру отклонения системы от состояния равновесия.

Концентрации фаз изменяются при их движении вдоль поверхности раздела, соответственно изменяется и движущая сила массопередачи, поэтому в уравнение массопередачи вводится величина средней движущей силы (

М =

М =

F 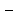поверхность контакта фаз (также обозначается буквой А).

Основное уравнение массопередачи может быть также представлено в следующих формах:

,

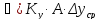
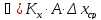
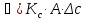где Δс 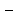разность концентраций.

Вместо ṅ (мольный расход вещества) может быть использована величина ṁ (массовый расход вещества).

Коэффициент массопередачи характеризует скорость процесса переноса вещества из одной фазы в другую; он показывает, какое количество (какая масса) распределяемого вещества переходит из фазы в фазу в единицу времени через единицу поверхности контакта фаз при движущей силе массопередачи, равной единице.

По физическому смыслу коэффициенты массопередачи отличаются от коэффициентов массоотдачи, но выражены в одинаковых с ними единицах измерения.

В зависимости от того, в каких единицах измерения выражается движущая сила процесса массопередачи, коэффициенты массопередачи могут иметь следующие размерности:

• движущая сила представляет собой разность объемных концентраций:

[]=[]

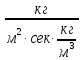• движущая сила представляет собой разность относительных концентраций:

[]=[]

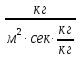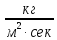• движущая сила представляет собой разность мольных долей:

[]

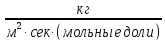• движущая сила представляет собой разность парциальных давлений (для газовой или паровой фазы):

[]=[]=[]=[]

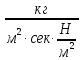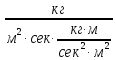В уравнение массопередачи может входить как масса, так и количество распределяемого вещества (переносимое в единицу времени в каждой из фаз). Если в уравнение массопередачи входит не масса (килограммы), а количество (киломоли) распределяемого вещества, то во всех приведенных выше единицах измерения килограммы должны быть заменены на киломоли.

Массоотдача 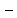конвективный массообмен между движущейся средой и поверхностью раздела с другой средой (иначе: перенос вещества от границы раздела фаз внутрь фазы). Скорость массоотдачи пропорциональна движущей силе, равной разности концентраций в ядре и на границе фазы или (в случае обратного направления переноса) 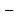разности концентраций на границе и в ядре фазы. Если распределяемое вещество переходит из фазы 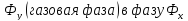(жидкая фаза), то основное уравнение массоотдачи, определяющее количество М вещества, переносимого в единицу времени в каждой из фаз (к границе фазы или в обратном направлении), можно представить в следующем виде:

М = (по газовой фазе) М = 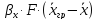(по жидкой фазе).

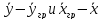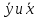
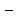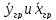
Входящие в эти уравнения разности концентраций представляют собой движущую силу процесса массоотдачи соответственно в фазах (жидкая фаза), причем средние концентрации в основной массе (ядре) каждой из фаз, концентрации у границы соответствующей фазы. Коэффициенты пропорциональности называются коэффициентами массоотдачи.

В отличие от коэффициента массопередачи, коэффициент массоотдачи характеризует скорость переноса вещества внутри фазы конвекцией и молекулярной диффузией одновременно. Коэффициент массоотдачи является не физической константой, а кинетической характеристикой и зависит от многих факторов:

• физических свойств фазы (плотность, вязкость и т.д.);

• гидродинамических условий в этой фазе (ламинарный или турбулентный режим течения);

• определяющих геометрических размеров и т.д.

Коэффициент массоотдачи показывает, какое количество вещества (какая масса вещества) переходит от единицы поверхности раздела фаз в ядро потока/фазы (или в обратном направлении) в единицу времени при движущей силе, равной единице.

По физическому смыслу коэффициенты массоотдачи отличаются от коэффициентов массопередачи, но выражены в одинаковых с ними единицах измерения (см. подраздел «Коэффициент массопередачи, его размерность и физический смысл»).

Коэффициент массоотдачи может быть выражен в различных единицах в зависимости от выбора единиц измерения для массы распределяемого вещества и движущей силы. Для перехода от величин коэффициентов массоотдачи, выраженных в 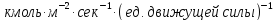, к их значениям в следует первые умножить на массу 1 кмоль (кг/кмоль) 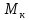распределяемого компонента.

Зависимость между коэффициентами массопередачи и массоотдачи можно выразить следующим образом:

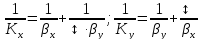
Вопрос №2: Метод кинетической линии рассчёта высоты массообменных аппаратов со ступенчатым контактом фаз. Порядок построения кинетической линии. Эффективность по Мэрфри.

ВОПРОС №3: Что такое теоретическая ступень разделения («теоретическая тарелка»)? Как это понятие применяется для оценки эффективности и расчета массообменных аппаратов со ступенчатым и непрерывным контактом фаз?

Теоретическая ступень разделения («теоретическая тарелка») – соответствуют некоторому гипотетическому участку аппарата, на котором жидкость полностью перемешивается, а концентрация удаляющихся фаз (например, жидкости и газа) являются равновесными.

Общую высоту H аппарата со ступенчатым контактом фаз с помощью числа теоретических ступеней определяют с использованием коэффициента полезного действия колоны η, который равен отношению числа теоретических ступеней к числу необходимых рабочих(действительных) ступеней N^{Дейстит.}. Тогда число действительных ступеней определяют из выражения N^{Дейстит.} = N^теор./ η. Определив N^{Дейстит.},рабочую высоту H аппарата со ступенчатым контактом фаз находят: h=( N^{Дейстит.} -1) h^т; h^т – расстояние между ступеньками, которое принимают или рассматривают. Расчет высоты h массообменных аппаратов с непрерывным контактом фаз можно проводить с помощью числа теоретических ступеней по формуле: h = h^экв. N^т.с.; N^т.с. – чисто теоретических ступеней; h^экв. – высота аппарата ( по разделяющему действию) одной ступени изменения концентрации(ВЭТС) или теоретической тарелке(ВЭТТ). ВЭТС и ВЭТТ определяются по эмпирическим зависимостям.

ВОПРОС №4: Диффузионное сопротивление массопереносу. В каких случаях сопротивление массопереносу лимитируется переносом в одной из фаз?

Уравнение массоотдачи показывает, какое количество вещества переносится из ядра потока к границе раздела фаз или в обратном направлении:

Уравнение массопередачи показывает, какое количество целевого компонента переходит в единицу времени из одной фазы в другую:

=> => ;

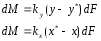
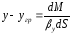
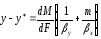но

Получим,

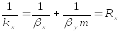
Если 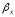очень велик то 1/ >> тогда 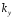= 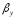сопротивление лимитируется в фазе Фy.

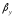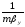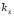Если очень велик то 1/ >> тогда = сопротивление лимитируется в фазе Фx.

ВОПРОС №5: Критерии подобия массообменных процессов. Их физический смысл.

Общность дифференциальных уравнений теплообмена

и массообмена

, (15.25)

позволяет полагать, что основные критерии массообменных процессов должны быть аналогичны основным критериям теплообмена.

Рассмотрим уравнения массопереноса на границе раздела фаз. Из одной фазы в другую переходит количество массы, равное

F(y – y*_гр),

где y*_гр равновесная концентрация на границе раздела фаз.

Это же количество массы переносится молекулярной диффузией через пограничный слой:

М =

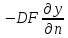
В этих уравнениях трудноопределимы величины y*_гр и n-тол­щина пограничного слоя, через который проходит вещество моле­кулярной диффузией. Отсюда

𝛽_y(y - y*_гр) =

или

𝛽_y∆y =

где

y - y*_гр = ∆y

Перемножим на масштабные множители каждый член послед­него уравнения:

α_𝛽 a_c (𝛽_y∆y) = (a_d a_c/a_l )

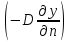
тогда

a_𝛽 a_l /a_d = 1

откуда

𝛽_l /D = Nu’

Где l - определяющий геометрический размер.

Данный безразмерный комплекс является аналогом теплового критерия Нуссельта (Nu = αl/λ,) и называется поэтому диффузион­ным критерием Нуссельта (иногда — критерием Шервуда Sh). Кри­терий Нуссельта Nu’ является oпределяемым критерием, поскольку в него входит величина𝛽. Так как Nu’ ~ 𝛽/D, то Nu’ характеризует отношение скорости переноса вещества (конвективного и молеку­лярного - 𝛽) к молекулярному переносу (D).

Другие критерии массообменных процессов получим из диф­ференциального уравнения конвективной диффузии (15.25). Пере­писав уравнение (15.25) относительно оси Х:

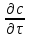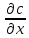+ w_x = D

И проведя его подобное преобразование, получим следующие кри­терии подобия:

τD/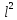 = Fo’-диффузионный критерий Фурье (аналог теплового критерия Фурье Fo = τα/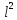), который характеризует подобие не­установившихся процессов массообмена;

Wl/D = Ре’-диффузионный критерий Пекле (аналог теплового критерия Пекле Ре = Wl/α).

Критерий Ре’ ~ W/D характеризует отношение переноса вещества конвекцией (W) к молекулярному переносу (D) в сходственных точках подобных систем. Часто критерий Ре’ заменяют отношением:

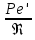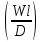= / = = Pr’

Диффузионный критерий Прандтля Рг’ является аналогом теп-ного критерия Рг = v/а (иногда критерий Рг’ называют критерием Шмидта Sc).

Формально критерий Рг’ выражает постоянство отношения физических свойств жидкости или газа в сходственных точках подобных систем. По существу же критерий Рг’ характеризует отношение профиля скоростей (через v) к профилю концентраций (через D), т. е. отношение толщины гидродинамического и диффузионного пограничных слоев.

Для соблюдения подобия процессов массоотдачи необходимо также соблюдение гидродинамического подобия. Поэтому критериальное уравнение массоотдачи для неустановившегося процесса имеют следующий вид (Г — геометрический симплекс)

Nu’ = f(Fo’, Re, Pr’, Ga, Г₁, Г₂ ...)

При установившемся процессе и при отсутствии влияния сил тяжести (т. е. при Fo’ = 0 и Ga =0):

Nu’ = f₁ (Re, Pr’, Г₁, Г₂...)

Например Nu’ = A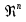( (15.30)

Где A, n, m, q, p  определяют опытным путем.

Уравнение (15.30) является обобщенным критериальным урав-инем массоотдачи. Поскольку оно аналогично критериальному уравнению теплоотдачи (11.35,а), то при одинаковых гидродинамических условиях

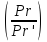= ^{^m} (15.31)

С помощью выражения (15.31) можно найти соотношение между коэффициентами тепло- и массоотдачи:

𝛽 = ^{^m} ,

которое позволяет по известному значению, например α, определить величину коэффициента массоотдачи 𝛽 при одних и тех же гидродинамических условиях.

ВОПРОС №6: Массообменный критерий Нуссельта. Каковы его вид и физический смысл?

Рассмотрим уравнения массопереноса на границе раздела фаз:

где β_y –коэффициент массоотдачи, F – поверхность, нормальная к направлению диффузии, y^*_гр – равновесная концентрация на границе раздела фаз.

Это же количество массы переносится молекулярной диффузией через пограничный слой:

D – коэффициент диффузии.

В этих уравнениях трудноопределимы величины y^*_гр и n – толщина пограничного слоя, через который проходит вещество молекулярной диффузией. Отсюда

или

где

Перемножим на масштабные множители каждый член последнего уравнения:

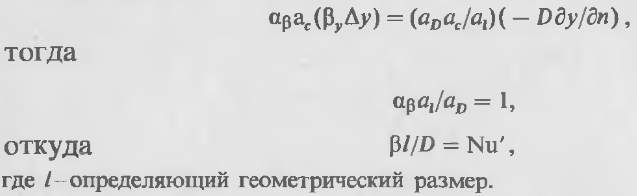Данный безразмерный комплекс является аналогом теплового критерия Нуссельта и называется поэтому диффузионным критерием Нуссельта. Критерий Нуссельта Nu’ является определяемым критерием, поскольку в него входит величина β. Так как Nu’ ~ β/D, то Nu' характеризует отношение скорости переноса вещества (конвективного и молекулярного – β) к молекулярному переносу (D).

ВОПРОС №7: Написать с необходимыми пояснениями и обозначениями выражение для расчёта средней движущей силы массопередачи в аппаратах с непрерывным контактом фаз при условии линейности рабочей и равновесной линий на примере абсорбции. Структура потоков идеального вытеснения.

ВОПРОС №8: Определение минимального и оптимального расхода поглотителя при абсорбции.

ВОПРОС №9: Гидродинамические режимы в насадочных аппаратах.

Рассмотрим гидродинамические режимы в насадочных колоннах, используя графическую зависимость гидравлического сопротивления орошаемой насадки от скорости газа в колонне

Зависимость гидравлического сопротивле­ния насадки от скорости газа в колонне (L = const):

1 сухая насадка; 2 - Орошаемая насадка

• Первый режим - Пленочный - наблюдается при небольших плотностях орошения на малых скоростях газа. В этом режиме отсутствует влияние газового потока на скорость стекания по насадке жидкой пленки и, следовательно, на количество задерживаемой в насадке жидкости. Пленочный режим заканчивается в первой переходной точке А На рис., называемой Точкой подвисания.

• Второй режим - Режим подвисания (или Торможения). После точки А Повышение скорости газа приводит к заметному увеличению сил трения о жидкость на поверхности контакта фаз и подтормаживанию жидкости газовым потоком. Вследствие этого скорость течения пленки жидкости уменьшается, а ее толщина и количество удерживаемой жидкости в насадке увеличиваются. В режиме подвисания с повышением скорости газа нарушается спокойное течение пленки жидкости, появляются завихрения, брызги, увеличивается смоченная поверхность насадки и соответственно-интенсивность процесса массопередачи. Этот режим заканчивается в точке В.

• Третий режим -режим эмульгирования - Возникает при превышении скорости, соответствующей точке В. В результате происходит накопление жидкости в свободном объеме насадки до тех пор, пока сила трения между стекающей жидкостью и поднимающимся по колонне газом не уравновесит силу тяжести жидкости, находящейся в насадке. При этом наступает обращение, или Инверсия, фаз (жидкость становится сплошной фазой, а газ-дисперсной). Образуется газожидкостная дисперсная система, по внешнему виду напоминающая барботажный слой (пену) или газожидкостную эмульсию. Режим эмульгирования начинается в самом узком сечении насадки, плотность засыпки которой неравномерна по сечению колонны. Путем тщательного регулирования подачи газа режим эмульгирования может быть установлен по всей высоте насадки (отрезок ВС На рис). Режим эмульгирования соответствует максимальной эффективности насадочных колонн преимущественно вследствие увеличении контакта фаз, который в этом режиме определяется не столько поверхностью насадочных тел, сколько поверхностью образующейся газожидкостной эмульсии, заполняющей весь свободный объем насадки. Следует отметить, что это повышение эффективности насадочной колонны сопровождается резким увеличением ее гидравлического сопротивления (отрезок ВС). В насадочных колоннах без специальных устройств поддерживать режим эмульгирования очень трудно, так как мал интервал изменения скоростей газа, при котором насадочная колонна работает в этом режиме (между точками В И С). Поэтому разработана специальная конструкция эмульгационной колонны. Как правило, работа в режиме подвисания и эмульгирования целесообразна только в случае, если повышение гидравлического сопротивления аппарата не имеет существенного значения (например, если абсорбер работает при повышенных давлениях). Поэтому большинство насадочных адсорберов работает в пленочном режиме (т. е. при скоростях газа до точки А). Пределом устойчивой работы насадочных колонн является скорость газа, соответствующая точке инверсии (или захлебывания).

• Четвертый режим- это режим уноса или обращенного движения жидкости, выносимой из аппарата газом (от точки С и выше). Этот режим в технике не используется.