
- •1. Линейная алгебра и аналитическая геометрия
- •2. Дифференциальное и интегральное исчисления
- •3. Функции нескольких переменных
- •4. Дифференциальные уравнения
- •5. Ряды
- •6. Теория вероятностей
- •1. Линейная алгебра и аналитическая геометрия Задача 1. Дана система линейных неоднородных алгебраических уравнений
- •2. Дифференциальное и интегральное исчисления
- •3. Функции нескольких переменных
- •4. Дифференциальные уравнения
- •5. Ряды
- •6. Теория вероятностей
3. Функции нескольких переменных
Задача
9. Проверить,
удовлетворяет ли уравнению
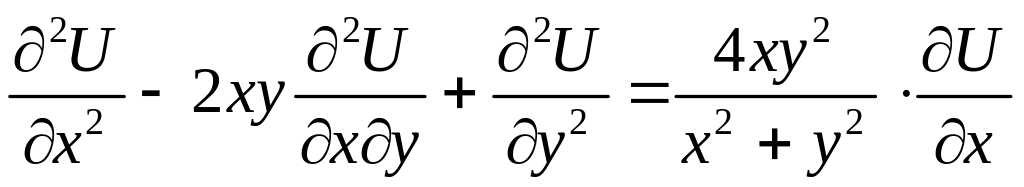 функция
функция
![]() .
.
Решение. Находим частные производные первого и второго порядка:
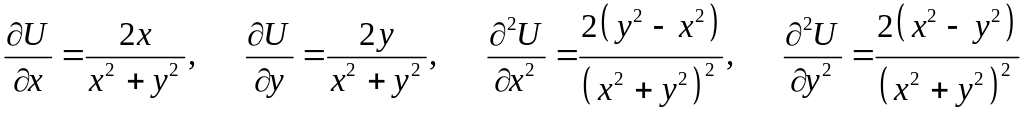 ,
,
 .
Подставляем полученные значения
производных в левую часть исходного
уравнения:
.
Подставляем полученные значения
производных в левую часть исходного
уравнения:
 .
.
В правой части
имеем:
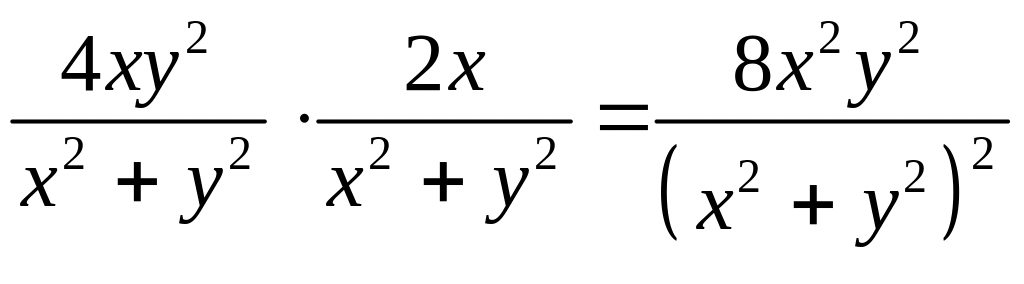 .
.
Сравнивая полученные результаты, видно, что данная функция удовлетворяет исходному уравнению.
Задача
10. Исследовать
на экстремум функцию
![]()
Решение. Находим первые частные производные данной функции:
![]() ,
,
 .
.
Приравнивая их к нулю, получаем систему уравнений:
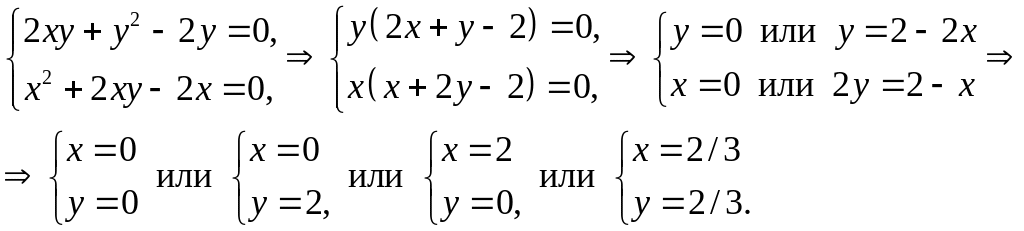
Получили
стационарные точки данной функции:
![]() .
Выясним, какие из этих точек являются
точками экстремума. Для этого вначале
найдем вторые частные производные
данной функции:
.
Выясним, какие из этих точек являются
точками экстремума. Для этого вначале
найдем вторые частные производные
данной функции:
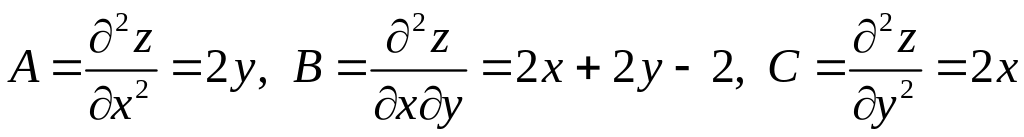 .
.
Составим определитель
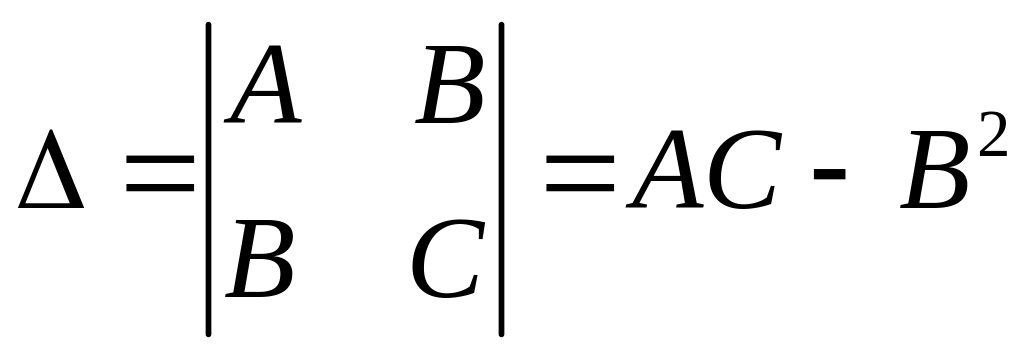 .
.
Подставляя в
![]() координаты стационарных точек и используя
достаточные условия экстремума, имеем:
для точки
координаты стационарных точек и используя
достаточные условия экстремума, имеем:
для точки
![]() ,
т.е. экстремума нет, для точки
,
т.е. экстремума нет, для точки
![]() ,
т.е. экстремума нет, для точки
,
т.е. экстремума нет, для точки
![]() ,
т.е. экстремума нет, для точки
,
т.е. экстремума нет, для точки
![]() и
и
![]() ,
т.е. имеем точку локального минимума
функции, в которой
,
т.е. имеем точку локального минимума
функции, в которой
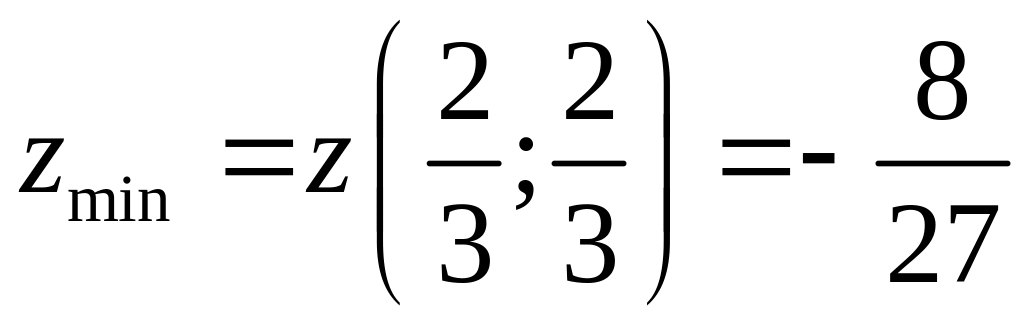 .
.
4. Дифференциальные уравнения
Задача
11. Найти
общее решение (общий интеграл)
дифференциального уравнения (особые
решения не рассматривать)
![]() .
.
Решение.
Заменим
![]() .
.
![]() .
Это уравнение с разделяющимися
переменными. Нужно умножить или разделить
обе части уравнения на такое выражение,
чтобы в одну часть уравнения входило
только
,
а в другую – только
.
Это уравнение с разделяющимися
переменными. Нужно умножить или разделить
обе части уравнения на такое выражение,
чтобы в одну часть уравнения входило
только
,
а в другую – только
![]() ,
и затем проинтегрировать обе части.
Умножим последнее уравнение на
,
и затем проинтегрировать обе части.
Умножим последнее уравнение на
![]() .
.
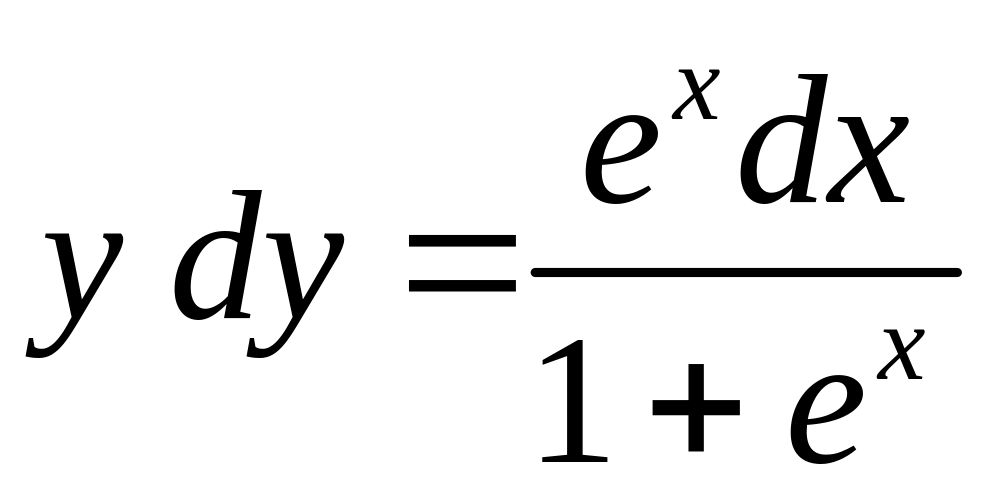 .
Интегрируем
.
Интегрируем
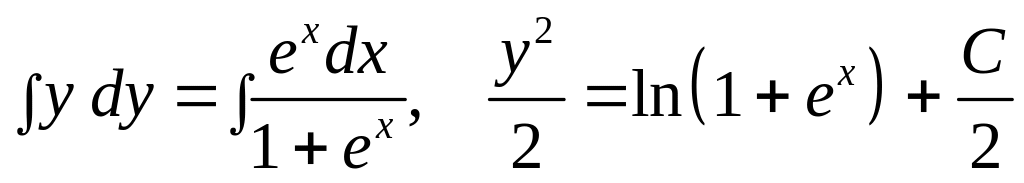 .
.
![]() – общий интеграл.
– общий интеграл.
Задача 12. Найти частное решение (частный интеграл) дифференциального уравнения, удовлетворяющее начальному условию
![]() .
.
Решение.
Разделим обе части уравнения на
![]() .
.
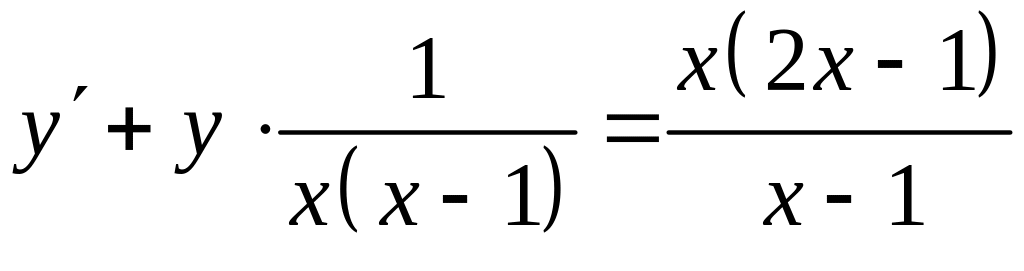 (*).
Это линейное дифференциальное уравнение
первого порядка. Решение ищем в виде
(*).
Это линейное дифференциальное уравнение
первого порядка. Решение ищем в виде
![]() ,
тогда
,
тогда
![]() .
Подставляем
и
в уравнение (*)
.
Подставляем
и
в уравнение (*)
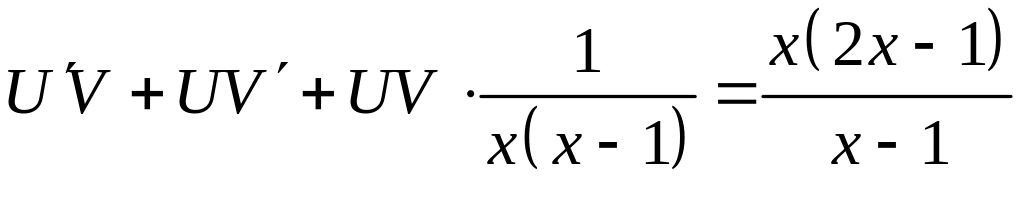 ,
,
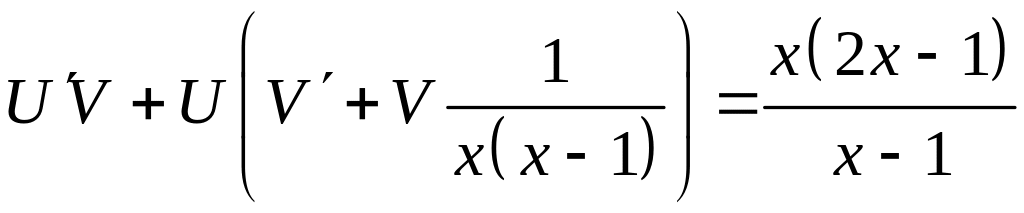 (**)
(**)
Функцию
![]() находим из условия
находим из условия
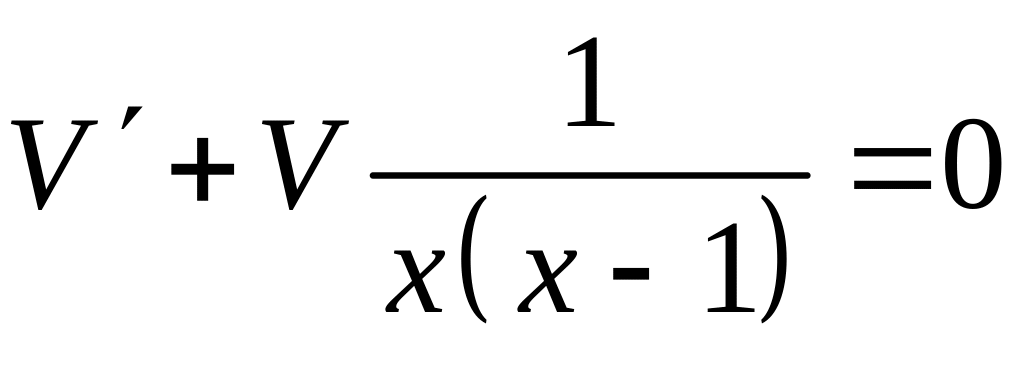
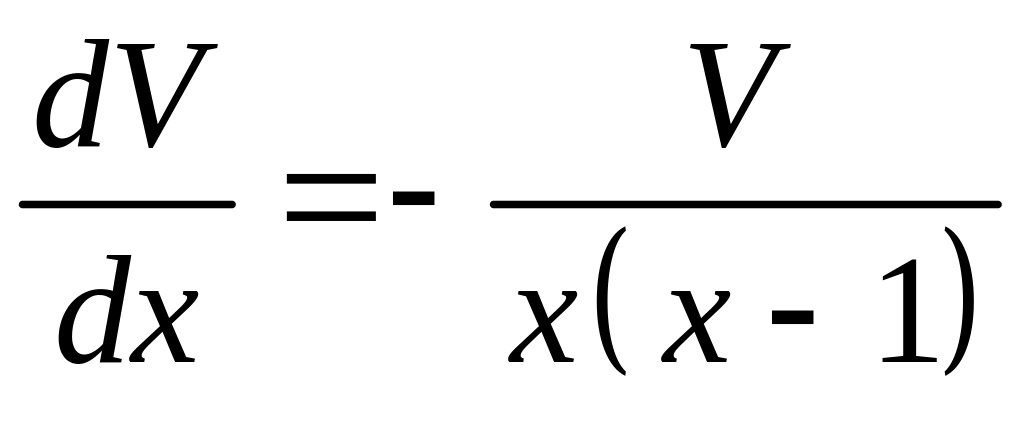 – это уравнение
с разделяющимися переменными.
– это уравнение
с разделяющимися переменными.
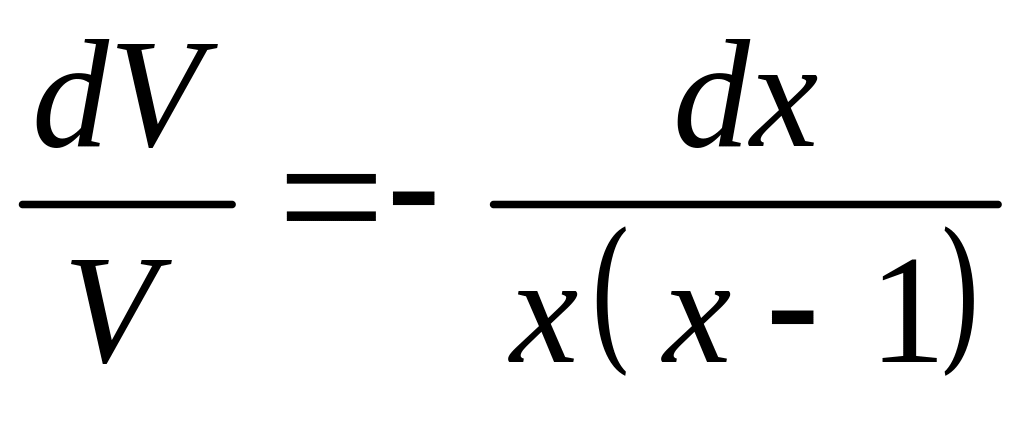 .
Интегрируем
.
Интегрируем
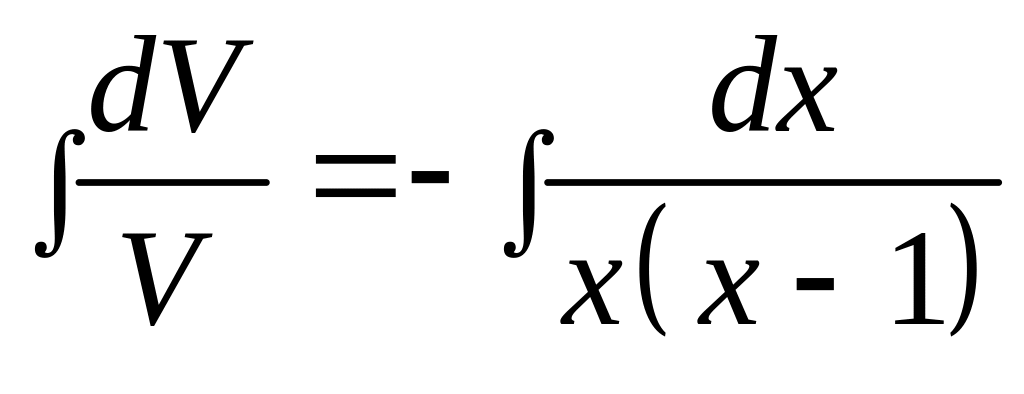 ,
,
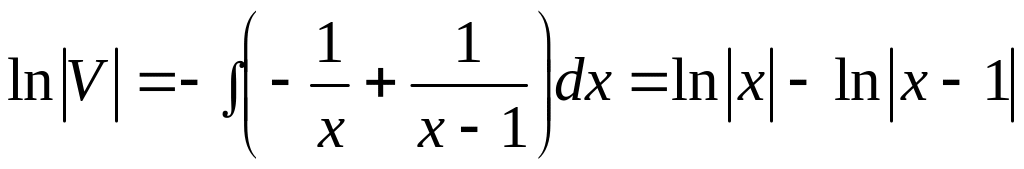 ,
,
![]() .
В качестве функции
взяли одно частное решение
.
В качестве функции
взяли одно частное решение
![]() .
Подставляем
в уравнение (**), получаем
.
Подставляем
в уравнение (**), получаем
![]() ,
,
![]() ,
тогда
,
тогда
![]() .
.
Следовательно, общее решение исходного уравнения
![]() .
Используя начальное условие
.
Используя начальное условие
![]() ,
,
найдем
:
![]() ,
откуда
,
откуда
![]() .
.
Частное решение
исходного уравнения будет
![]() .
.
Задача
13. Найти
общее решение дифференциального
уравнения, допускающего понижение
порядка
![]() .
.
Решение.
Уравнение не содержит искомой функции.
Введем новую функцию
![]() ,
тогда
,
тогда
![]() .
Исходное уравнение примет вид:
.
Исходное уравнение примет вид:
![]() .
.
Это
уравнение с разделяющимися переменными
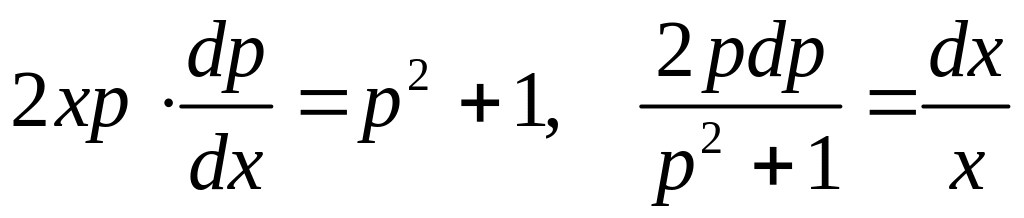 .
.
Интегрируем
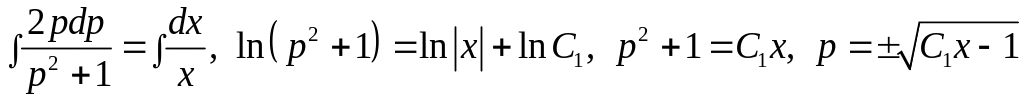 .
.
![]() .
.
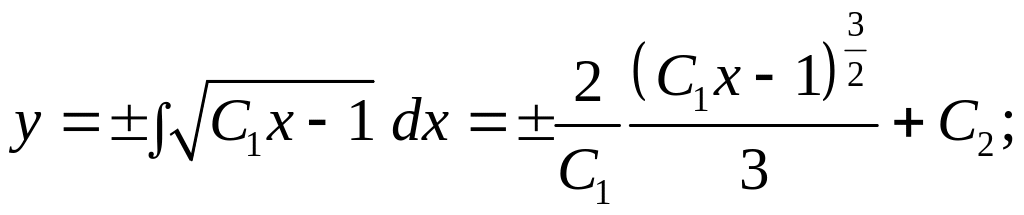
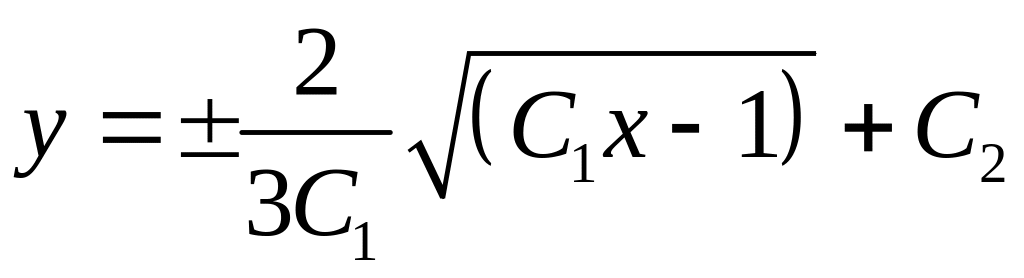 – общее решение.
– общее решение.
5. Ряды
Задача 14. Исследовать на сходимость заданный числовой ряд с положительными членами, используя достаточные признаки сходимости.
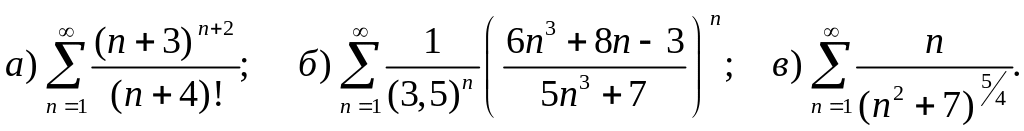
Решение. а) Используем признак Даламбера:
если
члены ряда
![]() положительны и
положительны и
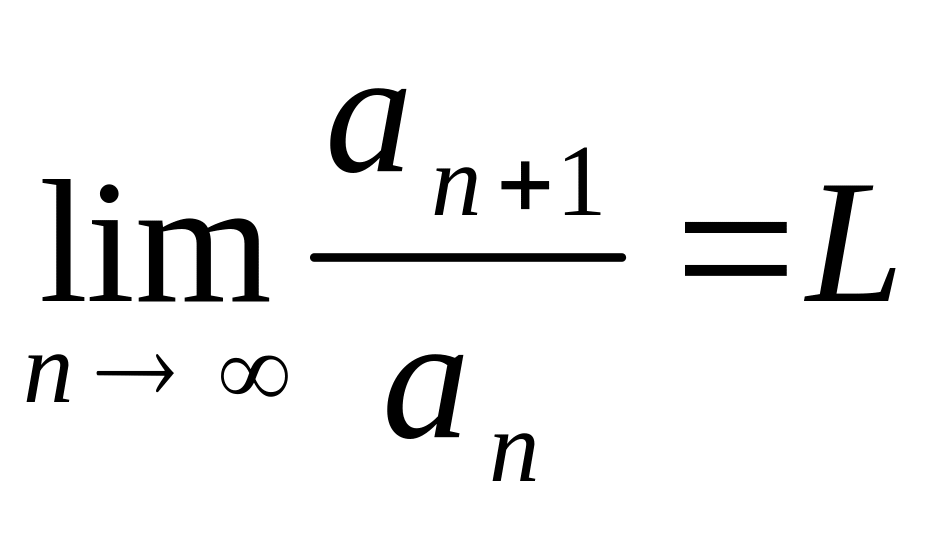 ,
то
,
то
при L < 1 ряд сходится, при L > 1 ряд расходится,
при L = 1 ряд нужно исследовать другими методами.
Записываем
общий член ряда
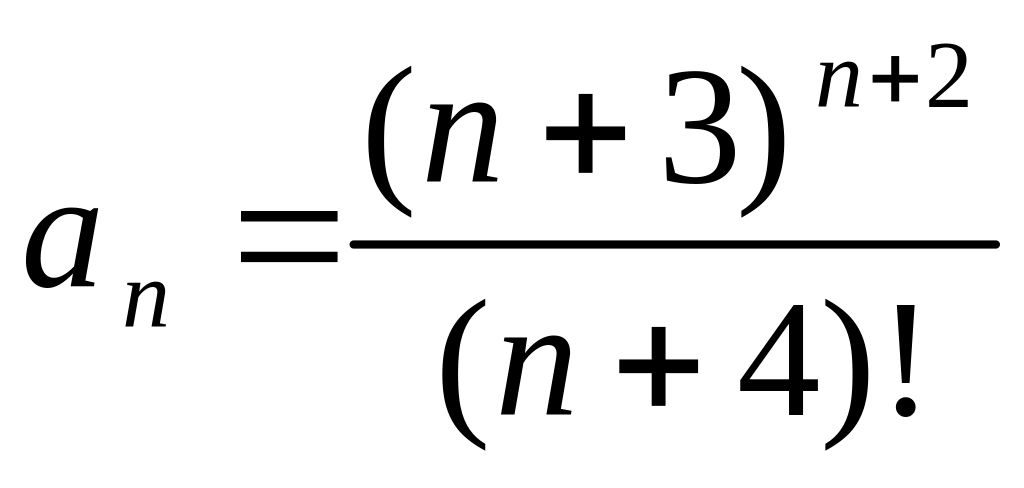 .
Член
.
Член
![]() получается из
получается из
![]() заменой номера n
на номер n
+ 1:
заменой номера n
на номер n
+ 1:
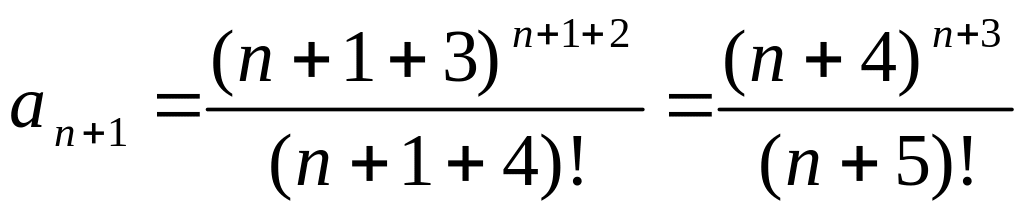 .
.
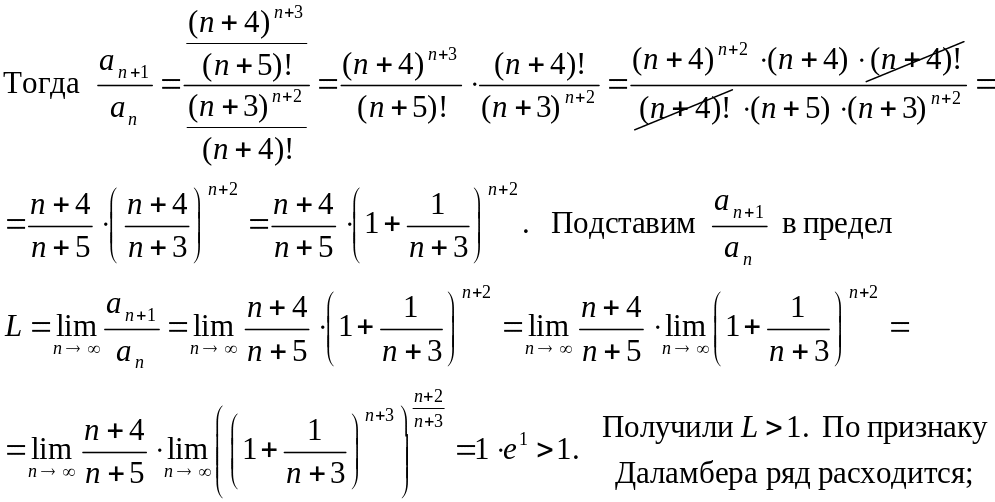
б) Используем радикальный признак Коши :
если
члены ряда
![]() положительны и
положительны и
![]() ,
то
,
то
при L < 1 ряд сходится, при L > 1 ряд расходится,
при L = 1 ряд нужно исследовать другими методами.
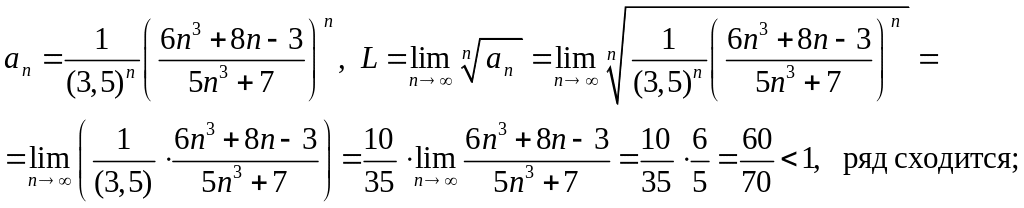
в)
Используем интегральный признак Коши.
Пусть члены ряда
убывают,
функция f
(x)
непрерывна на [a;+)
и
![]() .
Тогда
.
Тогда
если
несобственный интеграл
![]() сходится, то ряд
сходится,
сходится, то ряд
сходится,
если несобственный интеграл расходится, то ряд расходится.
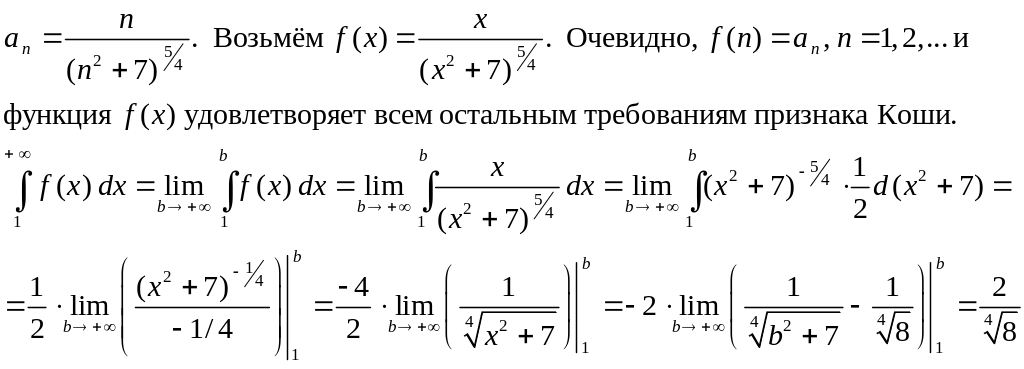
Несобственный интеграл сходится (имеет конечное значение), следовательно, ряд сходится.
Задача
15. Найти
область сходимости функционального
ряда
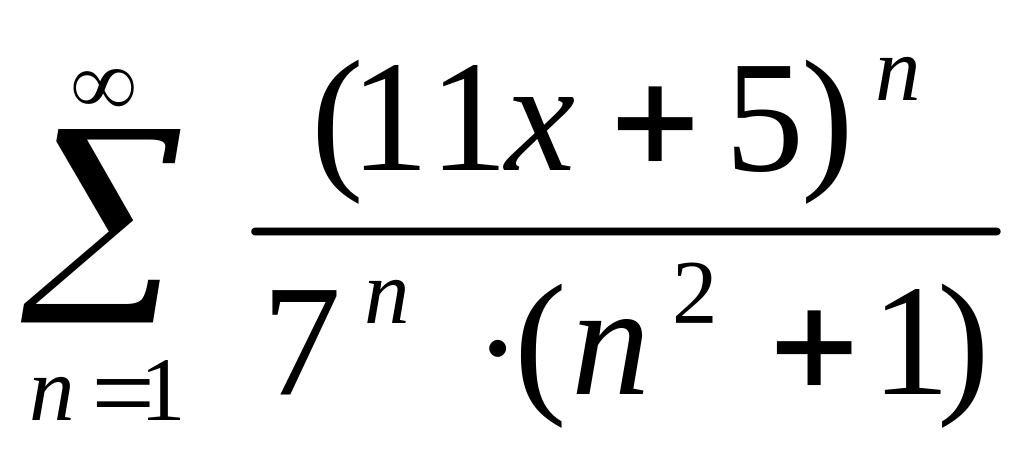 .
.
Решение.
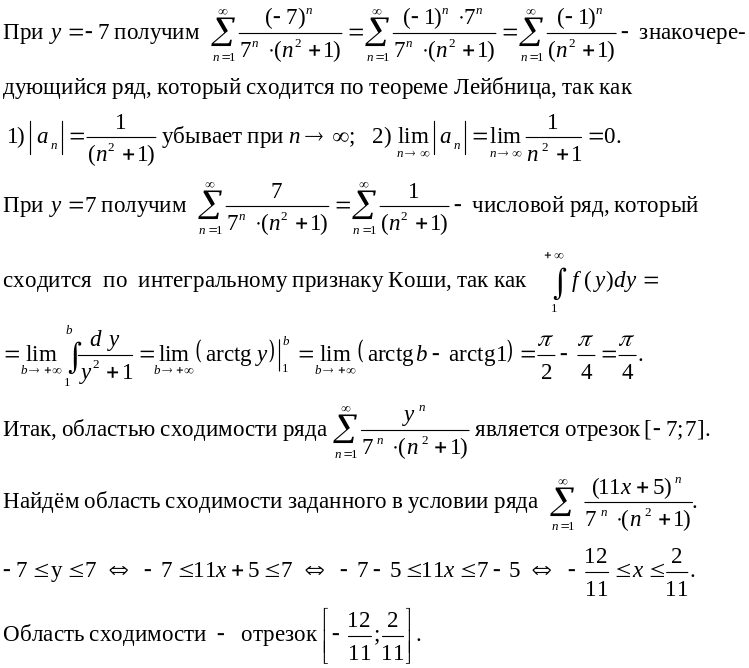
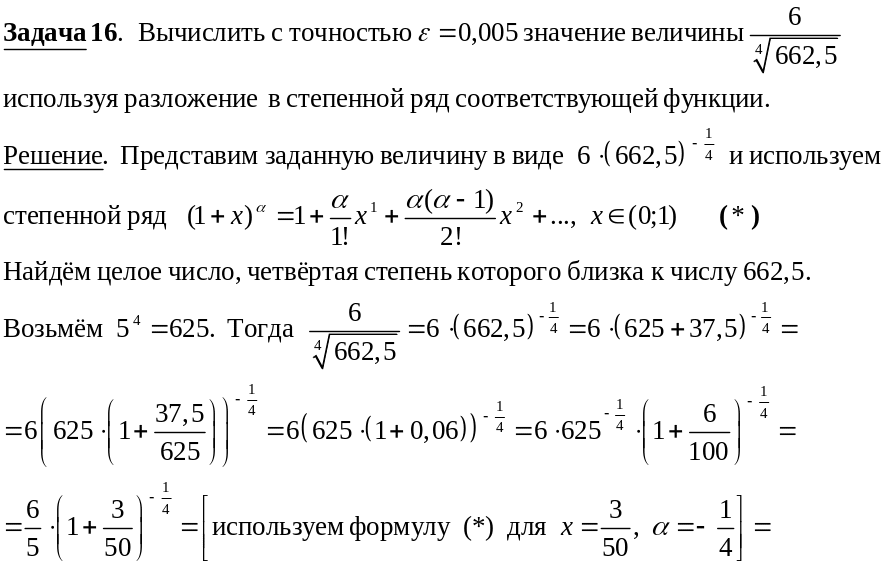
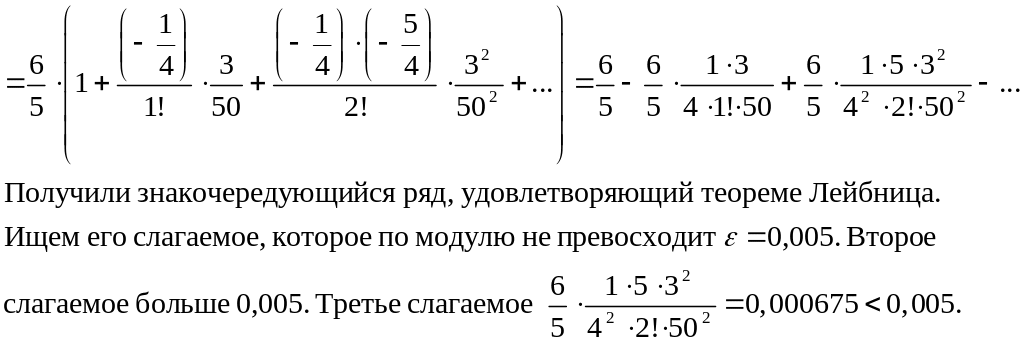
По
следствию из теоремы Лейбница, остаток
ряда, начинающийся с третьего слагаемого,
не превосходит числа
= 0,005 и, следовательно, сумма первых двух
слагаемых
![]() отличается от суммы ряда не более чем
на 0,005. Таким образом,
отличается от суммы ряда не более чем
на 0,005. Таким образом,

