
- •1. Линейная алгебра и аналитическая геометрия
- •2. Дифференциальное и интегральное исчисления
- •3. Функции нескольких переменных
- •4. Дифференциальные уравнения
- •5. Ряды
- •6. Теория вероятностей
- •1. Линейная алгебра и аналитическая геометрия Задача 1. Дана система линейных неоднородных алгебраических уравнений
- •2. Дифференциальное и интегральное исчисления
- •3. Функции нескольких переменных
- •4. Дифференциальные уравнения
- •5. Ряды
- •6. Теория вероятностей
1. Линейная алгебра и аналитическая геометрия Задача 1. Дана система линейных неоднородных алгебраических уравнений
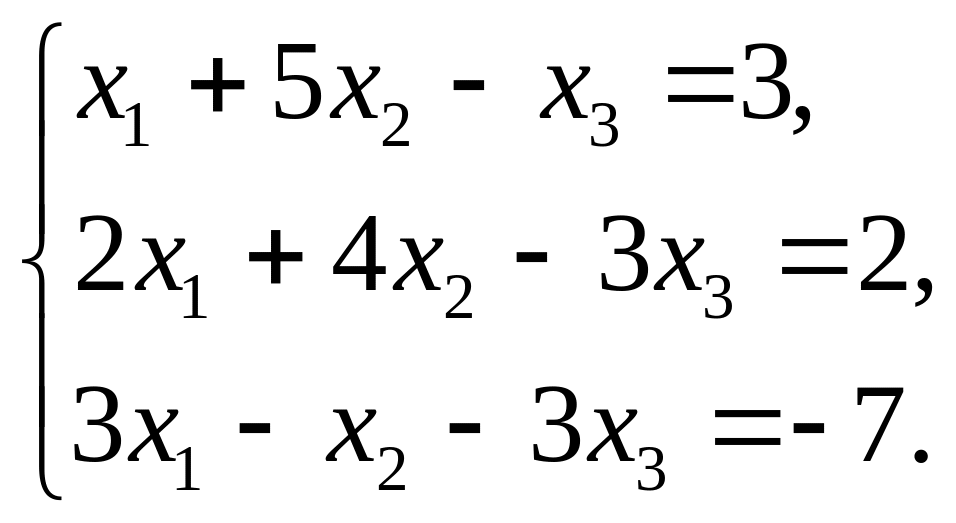
Зная, что система совместна, решим ее:
а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса.
Решение.
а)
По формулам Крамера
![]() ,
где
,
где
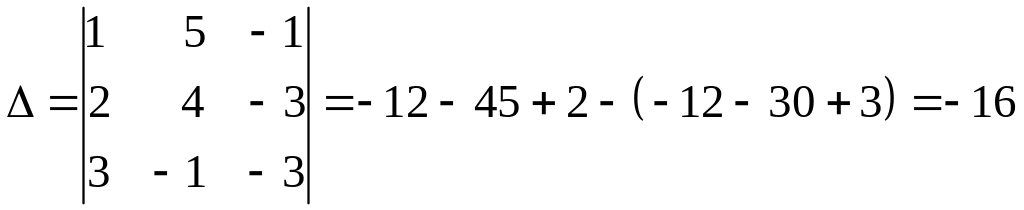 ;
;
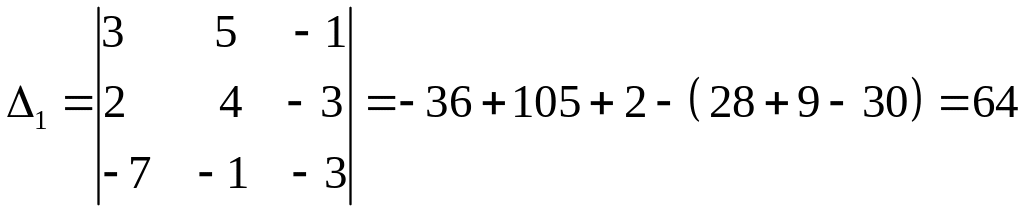 ;
;
 ;
;
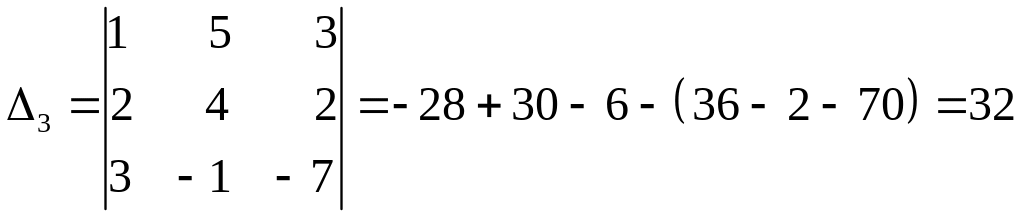 ,
,
находим:
![]() ;
;
б)
Для нахождения решения системы с помощью
обратной матрицы запишем систему
уравнений в матричной форме
![]() ,
,
где
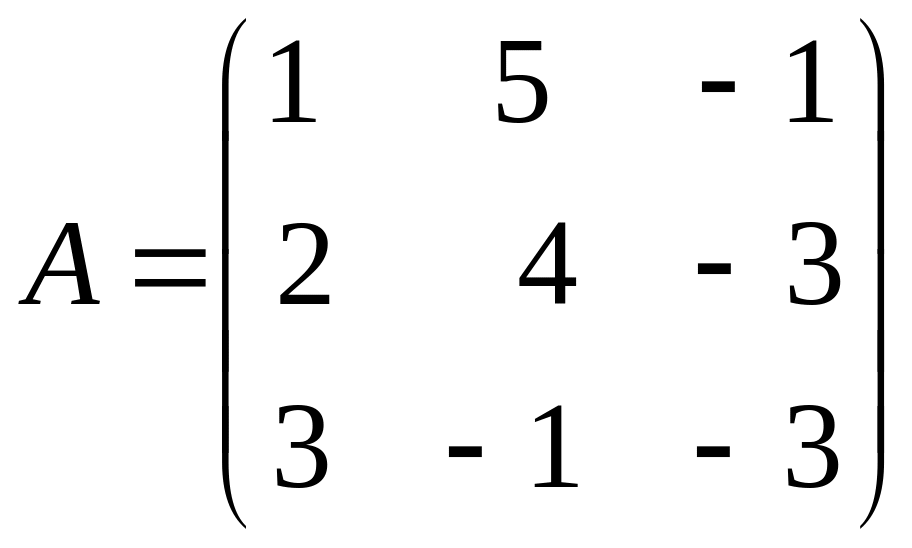 - основная матрица системы,
- основная матрица системы,
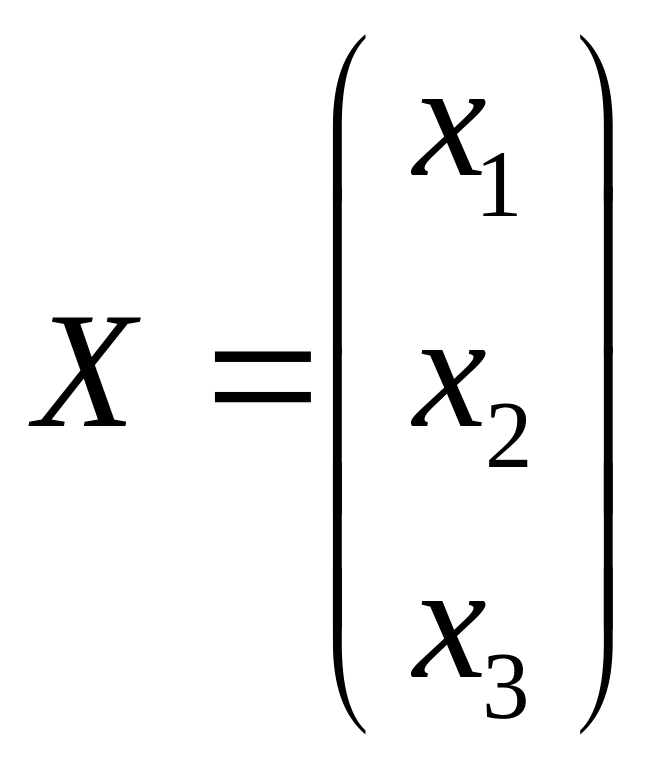 и
и
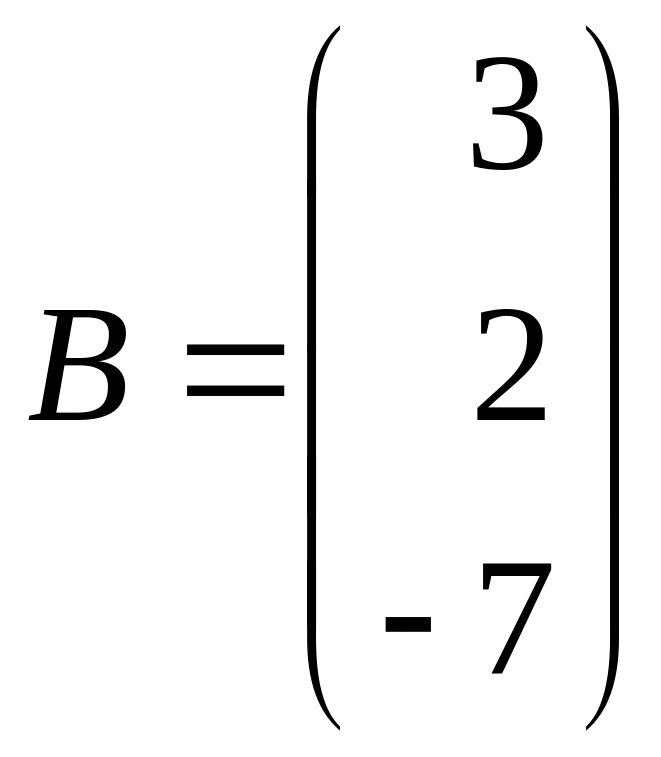 – матрицы-столбцы неизвестных и свободных
членов.
– матрицы-столбцы неизвестных и свободных
членов.
Решение системы
в матричной форме имеет вид
![]() ,
где
,
где
![]() - обратная матрица для невырожденной
матрицы
- обратная матрица для невырожденной
матрицы
![]() .
Матрица
определяется формулой
.
Матрица
определяется формулой
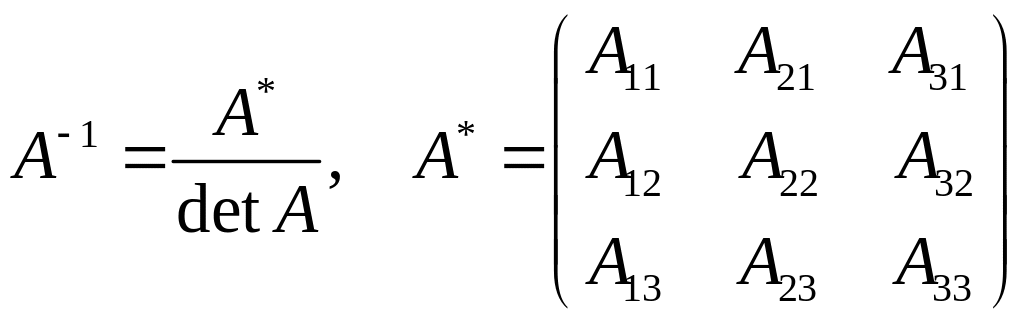 ,
где
,
где
![]() – присоединенная матрица, элементами
которой являются алгебраические
дополнения
– присоединенная матрица, элементами
которой являются алгебраические
дополнения
![]() элементов
элементов
![]() матрицы
.
матрицы
.
У нас
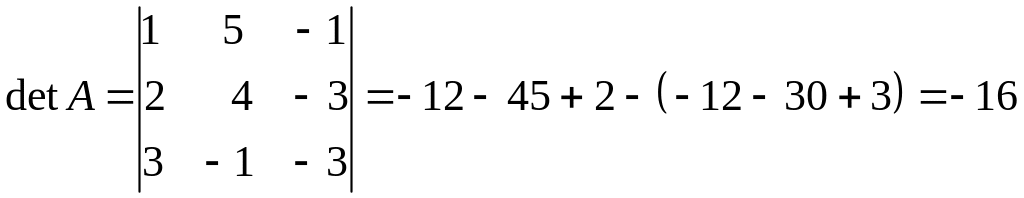 ,
,
т.е. матрица - невырожденная,
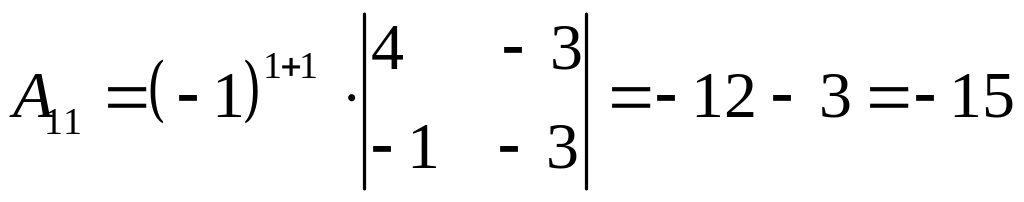 ,
,
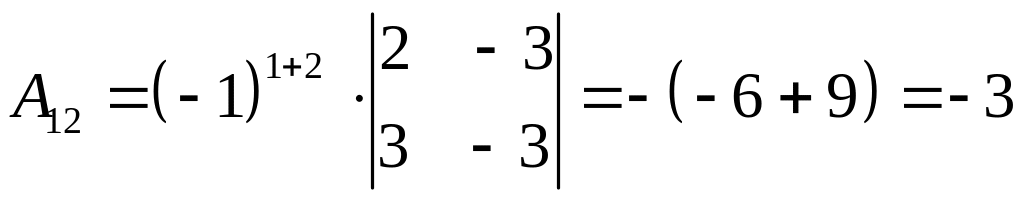 ,
,
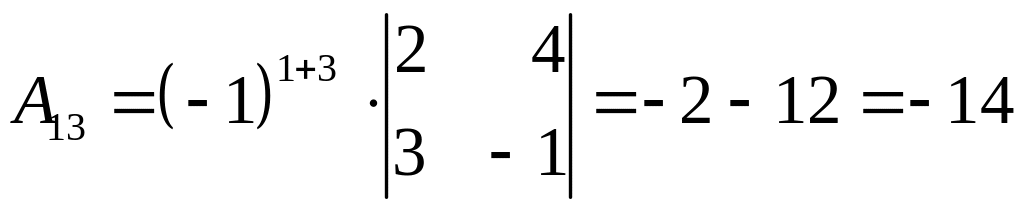 ,
,
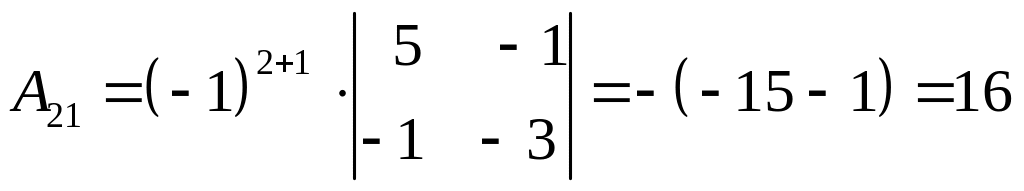 ,
,
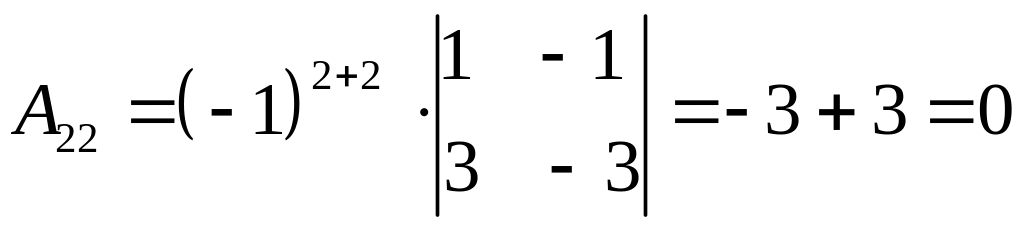 ,
,
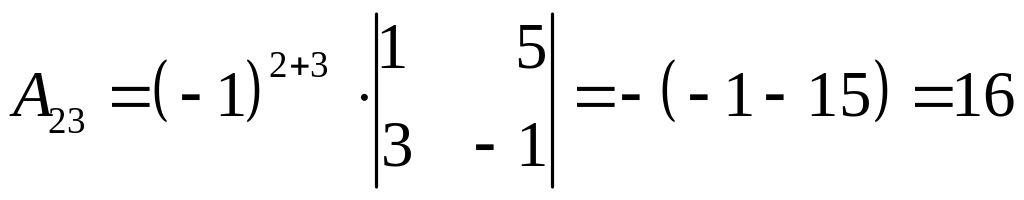 ,
,
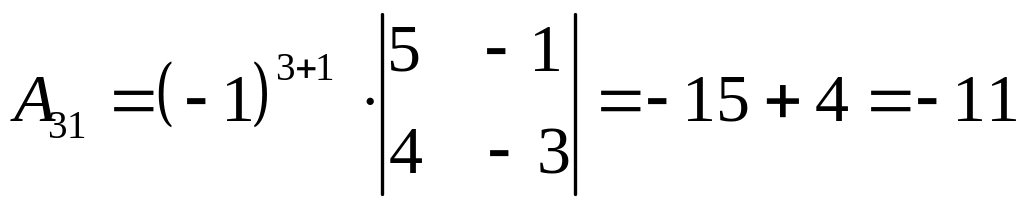 ,
,
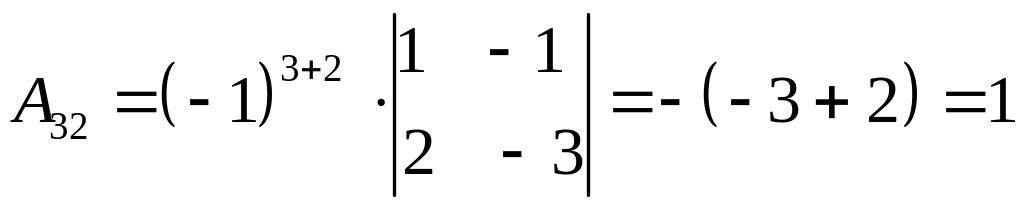 ,
,
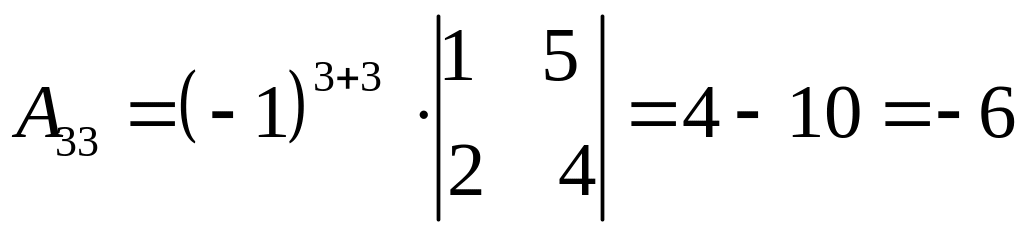 .
Тогда
.
Тогда
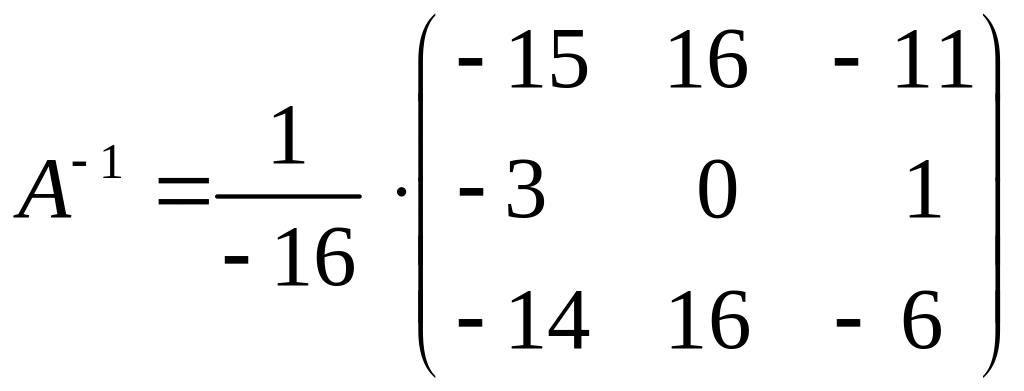 .
.
Решение системы:
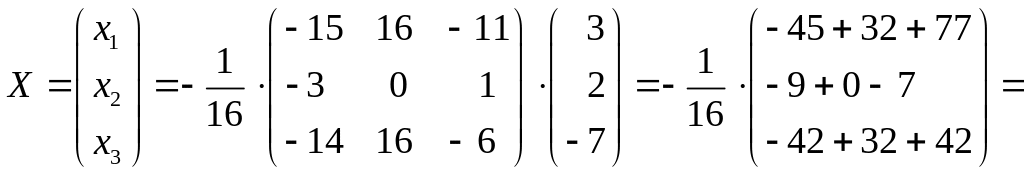
![]() .
.
То есть,
![]() ;
;
в)
Решим систему методом Гаусса. Для чего
составим расширенную матрицу системы
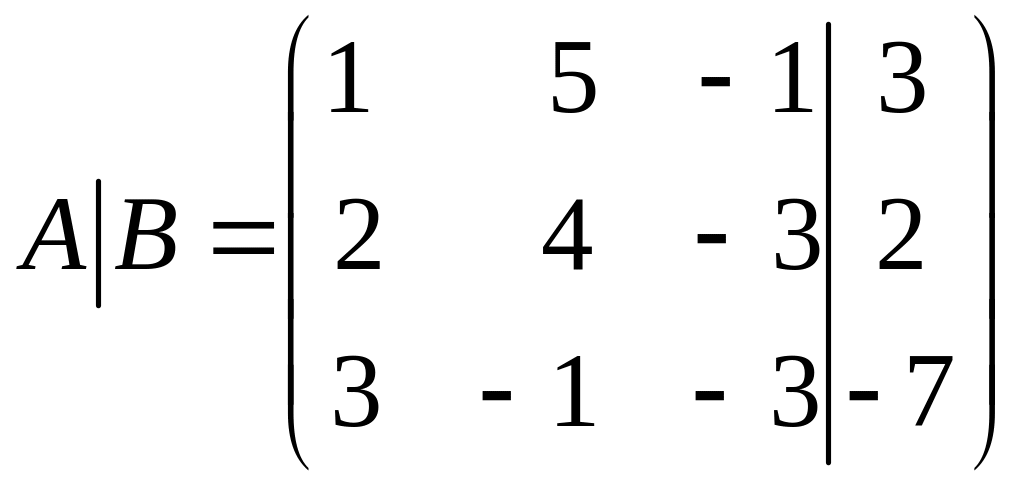 и проведем элементарные преобразования
строк: первую строку умножим на 2 и вычтем
из второй строки, затем первую строку
умножим на 3 и вычтем из третьей строки.
После чего разделим элементы третьей
строки на (–16).
и проведем элементарные преобразования
строк: первую строку умножим на 2 и вычтем
из второй строки, затем первую строку
умножим на 3 и вычтем из третьей строки.
После чего разделим элементы третьей
строки на (–16).
Имеем:
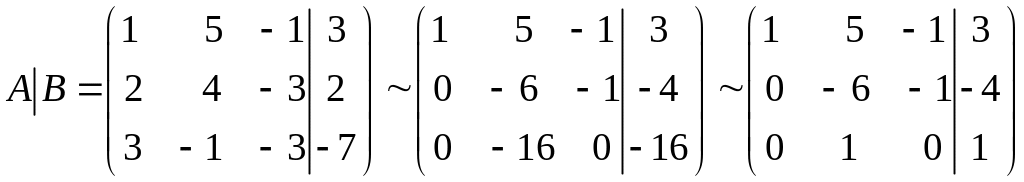 .
.
Полученной матрице,
эквивалентной заданной матрице
![]() ,
соответствует система уравнений
,
соответствует система уравнений
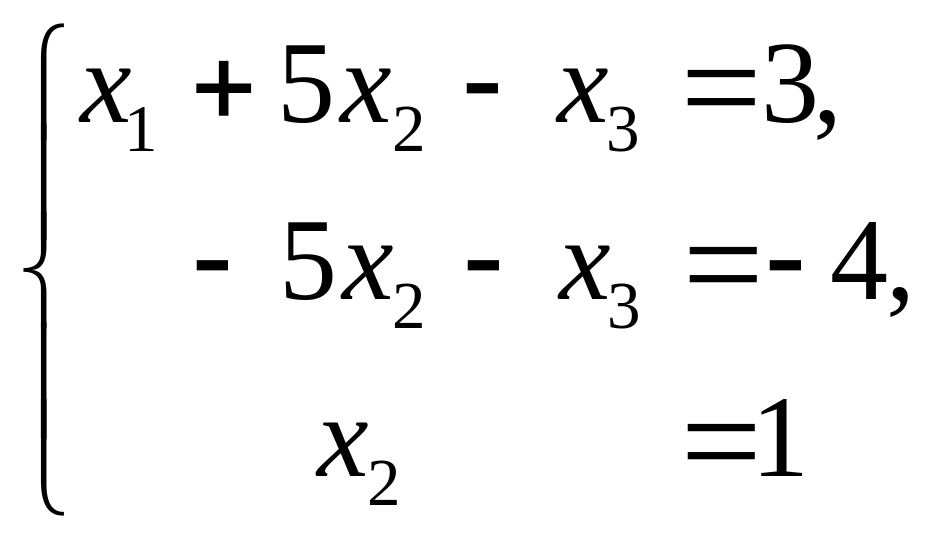 эквивалентная
исходной.
эквивалентная
исходной.
Из последнего
уравнения следует, что
![]() .
Подставив значение
.
Подставив значение
![]() во второе уравнение системы, получим
во второе уравнение системы, получим
![]() .
Подставив значения
и
.
Подставив значения
и
![]() в первое уравнение системы, получим
в первое уравнение системы, получим
![]() .
Итак,
.
Итак,
![]() .
.
Проверкой легко убедиться в правильности найденного решения.
Задача
2. Даны
вершины треугольника
![]() :
:
![]() .
Найти:
.
Найти:
а) уравнение стороны (записать общее и параметрические уравнения);
б) уравнение высоты (записать его в отрезках);
в) уравнение медианы (записать его в каноническом виде);
г) точку пересечения медианы и высоты ;
д) уравнение прямой, проходящей через вершину параллельно стороне (записать его в нормальном виде);
е) расстояние от точки до прямой .
Решение.
а)
Воспользовавшись уравнением прямой,
проходящей через две точки, получим
уравнение
:
![]() ,
откуда
,
откуда
![]() или
или
![]() – общее уравнение прямой
;
– общее уравнение прямой
;
и
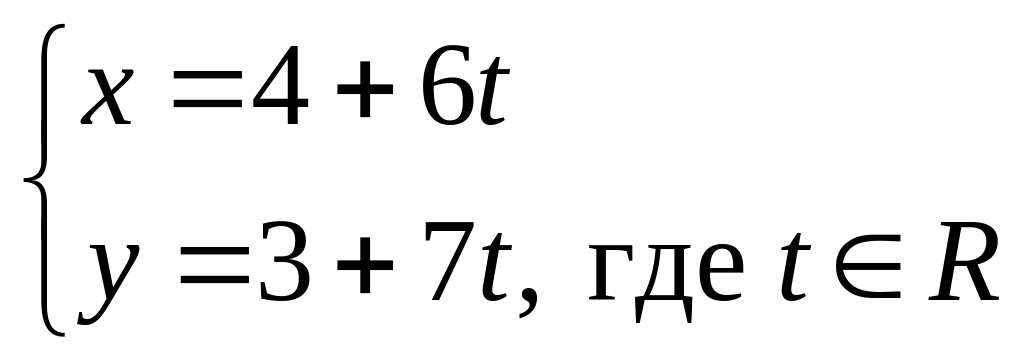 – параметрические уравнения прямой
;
– параметрические уравнения прямой
;
б)
Угловой коэффициент прямой
![]() .
С учетом перпендикулярности прямых
и
угловой коэффициент высоты
.
С учетом перпендикулярности прямых
и
угловой коэффициент высоты
![]()
![]() .
По точке
.
По точке
![]() и угловому коэффициенту
и угловому коэффициенту
![]() составляем уравнение высоты
:
составляем уравнение высоты
:
![]() или
или
![]() .
А в отрезках
.
А в отрезках
![]() ;
;
в)
Находим координаты
![]() середины
середины
![]() отрезка
отрезка
![]() :
:
![]() .
Теперь по двум известным точкам
и
составляем уравнение медианы
:
.
Теперь по двум известным точкам
и
составляем уравнение медианы
:
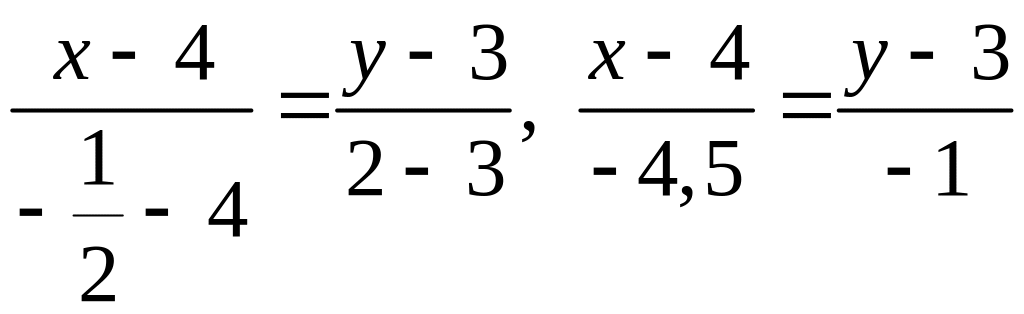 – каноническое
уравнение прямой;
– каноническое
уравнение прямой;
г)
Уравнение медианы
![]() ,
а высота
.
Для нахождения координат точки
пересечения этих прямых составляет
систему уравнений
,
а высота
.
Для нахождения координат точки
пересечения этих прямых составляет
систему уравнений
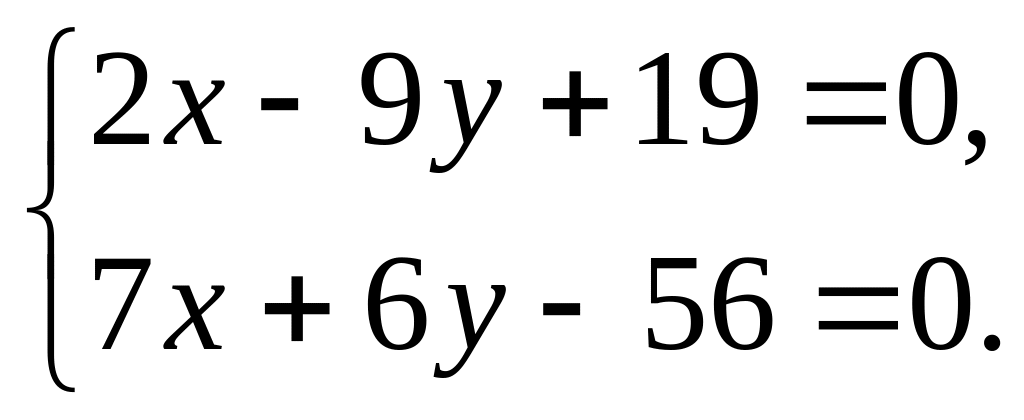 Решая ее, получаем
Решая ее, получаем
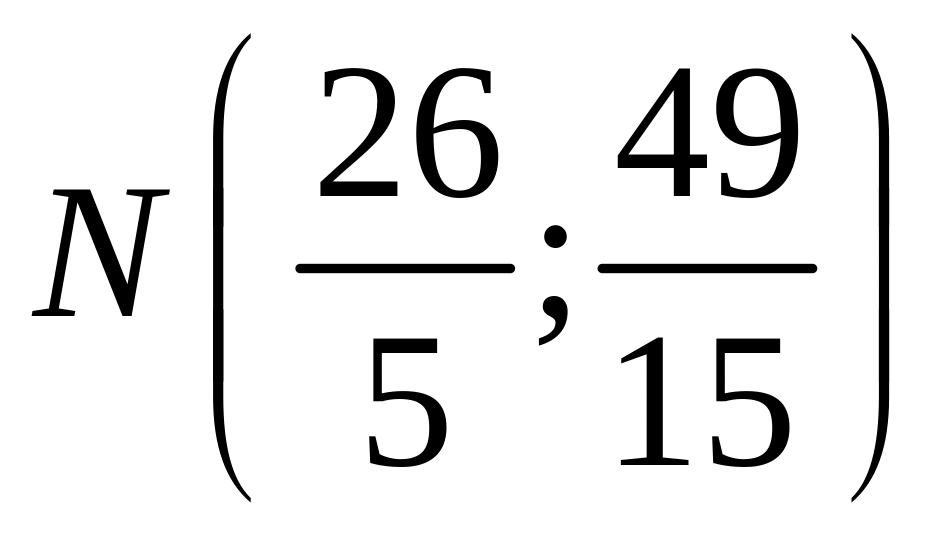 ;
;
д)
Так как прямая, проходящая через точку
,
параллельна стороне
,
то их угловые коэффициенты равны
.
Тогда по точке
и угловому коэффициенту
![]() составляем уравнение прямой
составляем уравнение прямой
![]() :
:
![]() или
или
![]() .
Чтобы привести его к нормальному виду,
введем нормирующий множитель
.
Чтобы привести его к нормальному виду,
введем нормирующий множитель
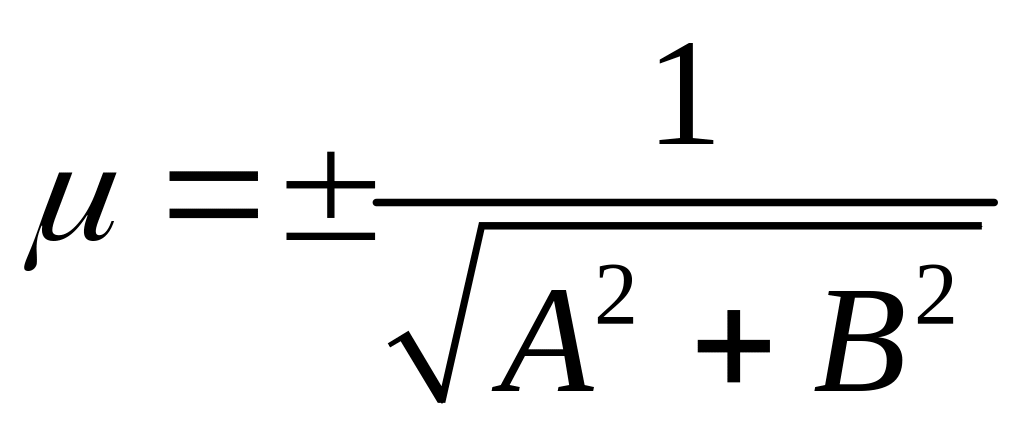 ,
где знак выбирается противоположным
знаку
в общем уравнении прямой
,
где знак выбирается противоположным
знаку
в общем уравнении прямой
![]() .
У нас
.
У нас
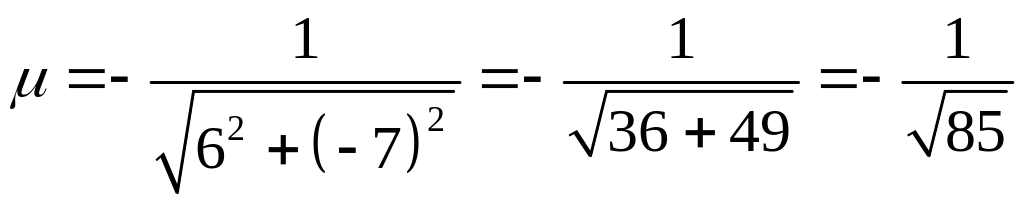 .
Тогда нормальное уравнение нашей прямой
имеет вид:
.
Тогда нормальное уравнение нашей прямой
имеет вид:
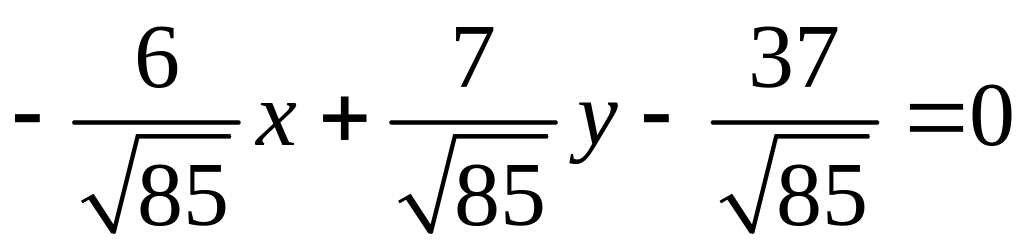 ;
;
е) Расстояние от точки до прямой вычисляем по формуле:
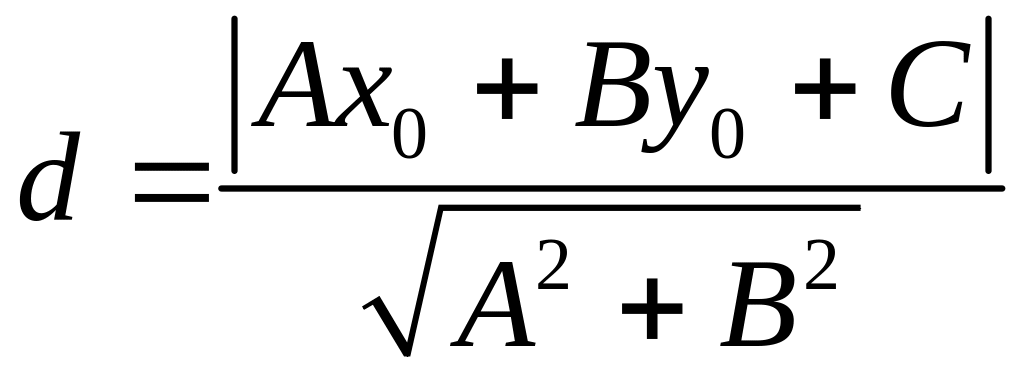
![]()
![]() ,
– уравнение заданной прямой. У нас
,
– уравнение заданной прямой. У нас
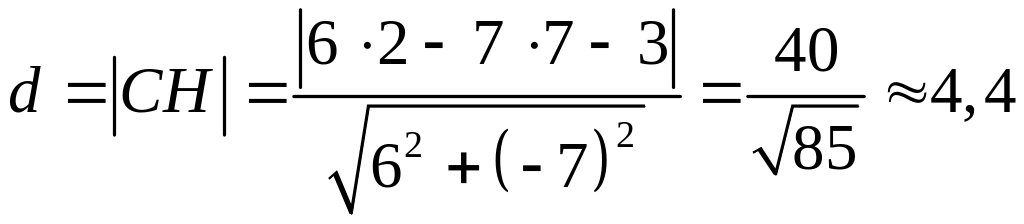 .
Решение задачи проиллюстрировано на
рисунке.
.
Решение задачи проиллюстрировано на
рисунке.

