
- •Содержание
- •«Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой»
- •Глава 1 пределы
- •Глава 2 дифференциальное исчисление функций одной независимой переменной
- •§ 1. Понятие производной
- •§2. Основные правила дифференцирования.
- •§3. Дифференцирование сложной функции.
- •§4. Производные высших порядков
- •§5. Дифференциал функции
- •Тогда, воспользовавшись формулой embed Equation.3 ,
- •§6. Применение производной при решении
- •Решение. Скорость прямолинейного движения
- •Глава 3 Исследование функций методами дифференциального исчисления
- •§1. Интервалы монотонности функции
- •Решение. Найдем производную заданной функции: embed Equation.3 .
- •§2. Экстремум функции
- •Глава 4 неопределенный интеграл4
- •§1. Непосредственное интегрирование.
- •Основные свойства неопределенного интеграла
- •§2.Интегрирование способом подстановки
- •§ 3. Интегрирование по частям.
- •Например:
- •§4. Применение неопределенного интеграла при решении прикладных задач.
- •Глава 5 определенный интеграл
- •§1.Определенный интеграл и его непосредственное
- •Основные свойства определенного интеграла
- •§2. Приложение определенного интеграла для вычисления площадей плоских фигур.
- •§3. Приложение определенного интеграла к решению физических задач.
- •Глава 6 дифференциальные уравнения
- •§1.Основные понятия.
- •§2.Уравнения с разделяющимися переменными.
- •§3. Однородные дифференциальные уравнения.
- •§4. Задачи на составление дифференциальных уравнений.
- •Глава 7 Элементы теории вероятностей и математической статистики
- •§ 1. Основные понятия
- •Вероятность случайного события – это количественная оценка объективной возможности появления данного события.
- •§ 2. Числовые характеристики распределения случайных величин
- •§4. Генеральная совокупность.
- •§5. Интервальная оценка. Интервальная оценка
- •§6. Проверка гипотез. Критерии значимости
- •§ 7. Элементы корреляционного и регрессионного анализа
- •7.1. Характер взаимосвязи между признаками
- •7.2. Проведение корреляционного анализа
- •7.3. Элементы регрессионного анализа
- •Статистическая обработка данных измерения роста.
- •Глава 4
- •Глава 5
- •Список литературы
- •614990, Г. Пермь,ул. Большевистская,85
§6. Применение производной при решении
прикладных задач
Производная
EMBED Equation.3
![]() от функции EMBED Equation.3
от функции EMBED Equation.3
![]() ,
вычисленная при значении аргумента
EMBED Equation.3
,
вычисленная при значении аргумента
EMBED Equation.3
![]() ,
представляет собой скорость изменения
этой функции относительно независимой
переменной EMBED Equation.3
,
представляет собой скорость изменения
этой функции относительно независимой
переменной EMBED Equation.3
![]() в точке EMBED Equation.3
.
в точке EMBED Equation.3
.
В
частности, если зависимость между
пройденным путем EMBED Equation.3
и временем EMBED Equation.3
![]() при прямолинейном движении выражается
формулой EMBED Equation.3
при прямолинейном движении выражается
формулой EMBED Equation.3
![]() ,
то скорость движения в любой момент
времени есть EMBED Equation.3
,
то скорость движения в любой момент
времени есть EMBED Equation.3
![]() ,
а ускорение, т.е. скорость изменения
скорости движения, EMBED Equation.3
,
а ускорение, т.е. скорость изменения
скорости движения, EMBED Equation.3
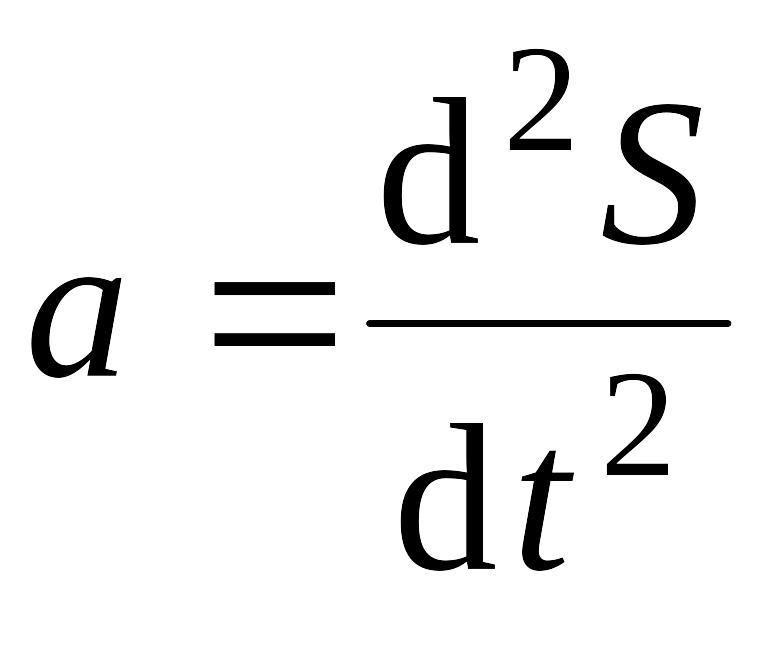 .
.
Например.
Точка движется прямолинейно по закону EMBED Equation.3
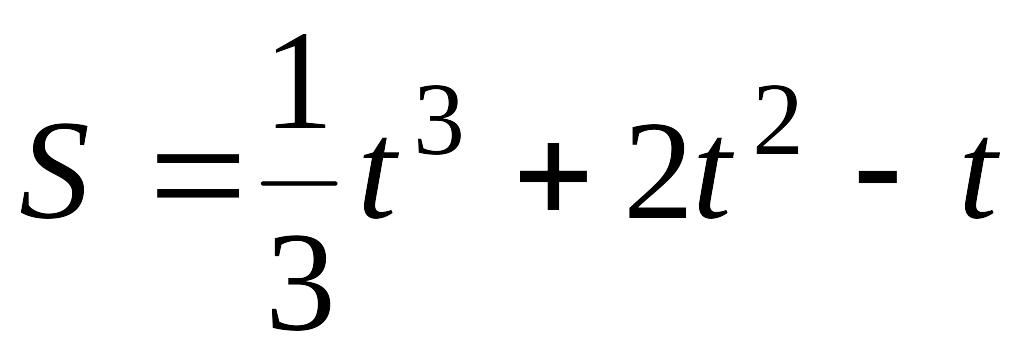 .
EMBED Equation.3
выражается в метрах, а EMBED Equation.3
- в секундах. (Обратите внимание на то,
что коэффициенты при соответствующих
степенях EMBED Equation.3
имеют разную размерность. Не забывайте,
что если слева стоят «метры», то и каждое
слагаемое в правой части должно тоже
иметь размерность «метры»). Найти
скорость и ускорение движения через 1
с после начала движения.
.
EMBED Equation.3
выражается в метрах, а EMBED Equation.3
- в секундах. (Обратите внимание на то,
что коэффициенты при соответствующих
степенях EMBED Equation.3
имеют разную размерность. Не забывайте,
что если слева стоят «метры», то и каждое
слагаемое в правой части должно тоже
иметь размерность «метры»). Найти
скорость и ускорение движения через 1
с после начала движения.
Решение. Скорость прямолинейного движения
EMBED
Equation.3
![]() .
.
Подставим
значение EMBED Equation.3
=1с
и получим EMBED Equation.3
![]() (м/с).
(м/с).
Ускорение
прямолинейного движения равно второй
производной пути по времени EMBED
Equation.3
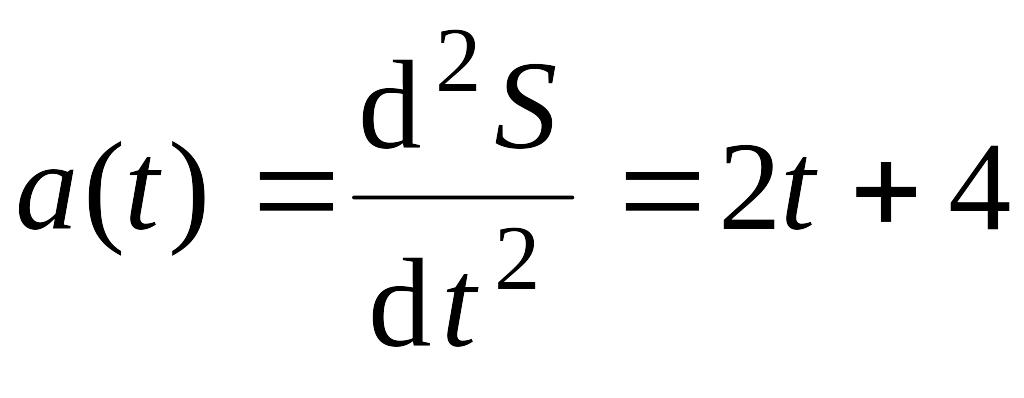 и, следовательно, EMBED Equation.3
и, следовательно, EMBED Equation.3
![]() (м/с2).
(м/с2).
Тело вращается вокруг неподвижной оси так, что угол его поворота меняется с течением времени по закону EMBED Equation.3
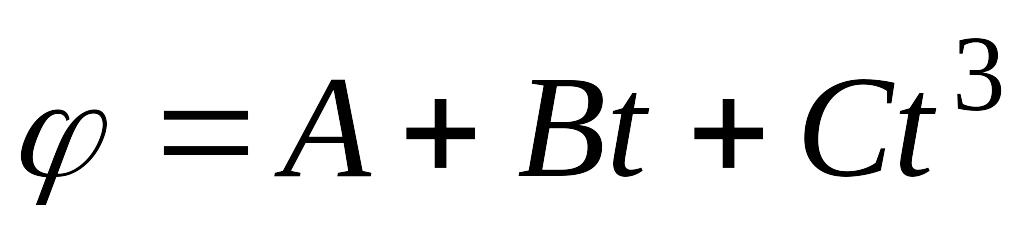 ,
где A, B,
C – постоянные
коэффициенты. Зная, что момент инерции
тела относительно оси вращения равен
EMBED Equation.3
,
где A, B,
C – постоянные
коэффициенты. Зная, что момент инерции
тела относительно оси вращения равен
EMBED Equation.3
 ,
найти момент сил М, действующий на
тело в любой момент времени.
,
найти момент сил М, действующий на
тело в любой момент времени.
Решение. Основной закон динамики вращательного движения записывается как
EMBED Equation.3
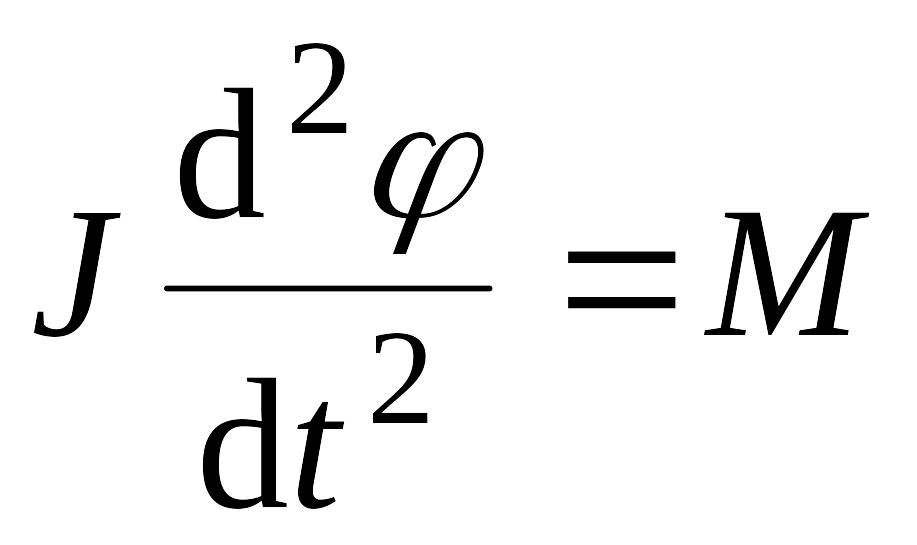 .
.
Искомый
момент сил М получим, подставив в
это уравнение угловое ускорение EMBED
Equation.3
![]() .
Угловая скорость EMBED Equation.3
.
Угловая скорость EMBED Equation.3
![]() ,
угловое ускорение EMBED Equation.3
,
угловое ускорение EMBED Equation.3
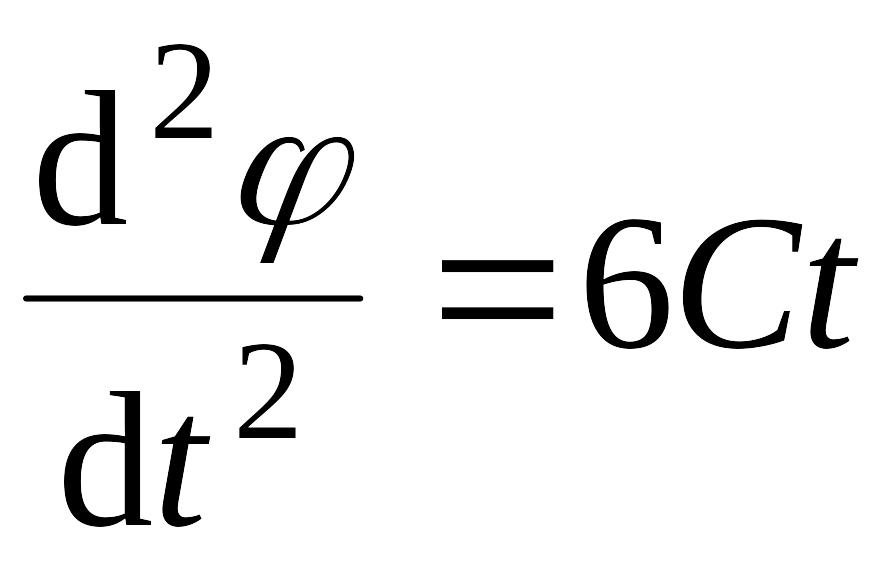 .
Отсюда EMBED Equation.3
.
Отсюда EMBED Equation.3
![]() .
.
Концентрация С некоторого вещества в крови человека вследствие его выведения из организма, изменяется с течением времени EMBED Equation.3 по закону EMBED Equation.3
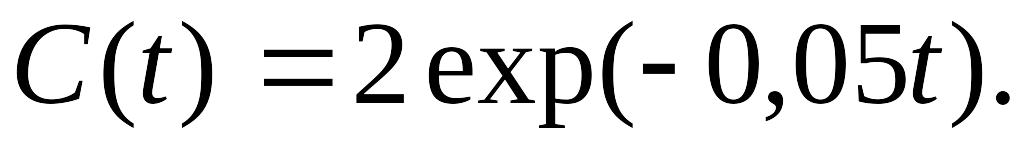 Определить скорость изменения
концентрации.
Определить скорость изменения
концентрации.
Решение. Скорость изменения концентрации определится как первая производная от концентрации по времени, т.е.
EMBED Equation.3
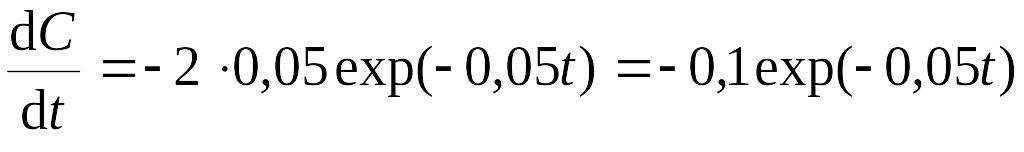 .
.
Решить задачи.
2.162.
Прямолинейное движение точки совершается
по закону EMBED Equation.3
![]() (м). Определить скорость в момент времени
EMBED Equation.3
(м). Определить скорость в момент времени
EMBED Equation.3
![]() с. (Ответ: v=27м/с).
с. (Ответ: v=27м/с).
2.163.
В какой момент времени скорость точки,
движущейся по закону EMBED Equation.3
![]() ,
равна нулю? (Ответ:
t=2
с).
,
равна нулю? (Ответ:
t=2
с).
2.164.
Зависимость пути от времени дается
уравнением EMBED Equation.3
![]() (м).
Найти скорость в конце второй секунды.
(Ответ: v=1,75
м/с).
(м).
Найти скорость в конце второй секунды.
(Ответ: v=1,75
м/с).
2.165.
При прямолинейном движении точки
зависимость пути от времени задана
уравнением EMBED Equation.3
![]() .
Найти ускорение точки в конце четвертой
секунды. (Ответ:
a=0,03
м/с2).
.
Найти ускорение точки в конце четвертой
секунды. (Ответ:
a=0,03
м/с2).
2.166. Точка движется по оси абсцисс по закону
EMBED Equation.3
 (м).
(м).
В какой момент времени точка остановится? (Ответ: точка остановится при t=3 c).
2.167. Точка движется по закону EMBED Equation.3 (м). Найти скорость и ускорение движения через 1 с после начала движения. (Ответ: v=4 м/с, a=6 м/с2).
2.168.
Диск вращается так, что угол поворота
его радиуса (в радианах) изменяется по
закону EMBED Equation.3
![]() ,
где B=2 рад/с2,
С=1рад/с3. Найти угловое ускорение
диска в любой момент времени, а также
момент силы, действующий на диск в любой
момент времени, если момент инерции
диска равен 0,02 кгм2.
(Ответ: =(2+3t)
c2;
M=0,04(2+3t)
нм).
,
где B=2 рад/с2,
С=1рад/с3. Найти угловое ускорение
диска в любой момент времени, а также
момент силы, действующий на диск в любой
момент времени, если момент инерции
диска равен 0,02 кгм2.
(Ответ: =(2+3t)
c2;
M=0,04(2+3t)
нм).
2.169.
Вращающееся колесо задерживается
тормозом. Угол, на который колесо
поворачивается в течение некоторого
времени, определяется выражением EMBED
Equation.3
![]() .
Найти угловую скорость и угловое
ускорение движения через 2 с после
включения тормоза. Определить, в какой
момент времени колесо остановится.
(Ответ: EMBED Equation.3
.
Найти угловую скорость и угловое
ускорение движения через 2 с после
включения тормоза. Определить, в какой
момент времени колесо остановится.
(Ответ: EMBED Equation.3
![]() с1,
EMBED Equation.3
с1,
EMBED Equation.3
![]() с2,
колесо остановится через t=0,2
c ).
с2,
колесо остановится через t=0,2
c ).
2.170.Уравнение вращательного движения твердого тела имеет вид: = A + Bt + Ct3, где A = 2 рад, B = 3 рад/с, C = 1 рад/с2.
Найти угол , угловую скорость и угловое ускорение в моменты времени t1=1 c, t2 = 4 c.
(Ответ:
EMBED
Equation.3
![]() ).
).
2.171.
Угловой путь вращающегося тела
задан уравнением
= 2t3 + 3t2
+ 8 (рад). Получить уравнение для углового
ускорения. (Ответ:
EMBED Equation.3
![]() ).
).
2.172.
Чему равна угловая скорость тела в конце
1-й секунды вращения, если точка,
расположенная на расстоянии 5 см от оси
вращения, движется по закону S=t2+2t
(м)? (Ответ: EMBED
Equation.3
![]() ).
).
2.173.
Чему равна угловая скорость тела в конце
2-ой секунды вращения, если точка,
расположенная на расстоянии R
= 5 см от оси вращения, движется по закону
S = 4 t2
+ 4t (м ) ?
(Ответ: EMBED Equation.3
![]() ).
).
2.174.
Определить угловые скорость и ускорение
тела, если угловой путь задан уравнением
= at2
+ b ( рад).
(Ответ: EMBED Equation.3
![]() ).
).
2.175.
Определить угловое ускорение тела, если
линейная скорость точки, движущейся по
окружности R=10см, задана
уравнением v = 2t
+ 4 (м/с). (Ответ:
EMBED Equation.3
![]() ).
).
2.176.
Какую угловую скорость будет иметь тело
к концу второй секунды, если вращение
задано уравнением
= 2 t2 + 4t
(рад). (Ответ: EMBED
Equation.3
![]() ).
).
2.177.
Определить угловое ускорение тела,
если линейная скорость точки, движущейся
по окружности R=0,2 см,
задана уравнением v = 3t
+ 4 (м/с). (Ответ:
EMBED Equation.3
![]() ).
).
2.178.
Материальная точка вращается по
окружности радиусом R= 2м
по закону S = 3t2
(м). Определить ее угловое ускорение.
(Ответ: EMBED Equation.3
![]() ).
).
2.179.
Уравнение вращения тела имеет вид
= t3
+ 4 . Найти угловое ускорение тела в
момент времени t = 3 с.
(Ответ: EMBED Equation.3
![]() ).
).
2.180.
Угловой путь вращающегося тела задан
уравнением = t3
+ 2t2 + 4. Найти
уравнение для углового ускорения.
(Ответ: EMBED Equation.3
![]() ).
).
2.181.
Чему равна угловая скорость тела в конце
1-й секунды вращения, если точка,
расположенная на расстоянии 10 см от оси
вращения, движется по закону S
= 2t2 + 4t
(м). (Ответ: EMBED
Equation.3
![]() ).
).
2.182. Какую угловую скорость будет иметь тело к концу второй секунды, если вращение задано уравнением = 2t2 + 4t? (Ответ: EMBED Equation.3 ).
2.183. Определить угловое ускорение тела, если линейная скорость точки с радиусом-вектором 0,2 см задана уравнением V = 3t + 4 ( м/с). (Ответ: EMBED Equation.3 ).
2.184.
Момент импульса тела с течением времени
изменяется по закону L=4t+2(кгм/с).
Определить момент сил, действующих на
тело. (Ответ:
EMBED Equation.3
![]() ).
).
2.185.
Тело колеблется по закону EMBED Equation.3
![]() (м).
Найти скорость тела в момент времени
EMBED Equation.3
(м).
Найти скорость тела в момент времени
EMBED Equation.3
![]() .(Ответ:
v=0,57
м/с).
.(Ответ:
v=0,57
м/с).
2.186.
Точка участвует в движении, заданном
уравнением EMBED Equation.3
![]() (м). Найти скорость и ускорение в момент
времени EMBED Equation.3
(м). Найти скорость и ускорение в момент
времени EMBED Equation.3
![]() .(Ответ:
v=26,4
м/с, a=252
м/с2).
.(Ответ:
v=26,4
м/с, a=252
м/с2).
2.187.
Тело массой 1 г колеблется по закону
EMBED Equation.3
![]() (м).
Найти силу, действующую на тело в любой
момент времени, и ее максимальное
значение. Вычислить это значение при
EMBED Equation.3
(м).
Найти силу, действующую на тело в любой
момент времени, и ее максимальное
значение. Вычислить это значение при
EMBED Equation.3
![]() =3104Гц.
=3104Гц.
(Ответ:
EMBED Equation.3
![]() Н, EMBED Equation.3
Н, EMBED Equation.3
![]() Н,
EMBED Equation.3
Н,
EMBED Equation.3
![]() Н).
Н).
2.188.
Тело массой 25 кг движется по закону
EMBED Equation.3
![]() .
Найти кинетическую энергию тела через
2 с после начала движения.
.
Найти кинетическую энергию тела через
2 с после начала движения.
(Ответ
EMBED Equation.3
![]() ).
).
2.189.
Центр тяжести кисти человека при ходьбе
совершает колебания по закону EMBED
Equation.3
![]() (м).
Определить максимальные скорость и
ускорение центра тяжести кисти, а также
период колебания. (Ответ:
EMBED Equation.3
(м).
Определить максимальные скорость и
ускорение центра тяжести кисти, а также
период колебания. (Ответ:
EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() ).
).
2.190.Тело
движется по закону EMBED Equation.3
![]() .
Найти ускорение для любого момента
времени. (Ответ:
EMBED Equation.3
.
Найти ускорение для любого момента
времени. (Ответ:
EMBED Equation.3
![]() ).
).
2.191.
Гармоническое колебание задано уравнением
X=5
cos
(2+/4)
(см). Получить уравнение для расчета
скорости. Чему равна амплитуда скорости?
(Ответ: EMBED Equation.3
![]() ).
).
2.192.
Гармоническое колебание задано уравнением
X=5
cos
( +/6)
(см). Определить амплитуду скорости. Для
каких значений X
скорость максимальна? (Ответ:
EMBED Equation.3
![]() ).
).
2.193. Уравнение для смещения гармонического колебательно движения задано в виде X=5 cos ( 2t+/2) ( мм). Найти выражение для ускорения. Результат представить в системе "СИ".
(Ответ:
EMBED Equation.3
![]() ).
).
2.194.
Уравнение для смещения при гармоническом
колебании задано в виде X=2cos(t+/4)
( м ). Найти закон изменения ускорения и
построить график ускорения для этого
движения. (Ответ:
EMBED Equation.3
![]() ).
).
2.195.
Скорость гармонического колебательного
движения задана уравнением
V=-sin(2t+/4)(м/с).
Найти закон изменения ускорения и
построить его график. (Ответ:
EMBED Equation.3
![]() ).
).
2.196.
Точка совершает
гармонические колебания по закону
синуса с амплитудой 10 см и периодом 0,2
с. Найти максимальное значение ускорения.
Как изменится результат, если колебания
будут происходить по закону косинуса?
(Ответ:
EMBED Equation.3
![]() .
Если колебания
будут происходить по закону косинуса,
результат не изменится).
.
Если колебания
будут происходить по закону косинуса,
результат не изменится).
2.197.
Тело массой 1 г колеблется по закону
X=2cos(2t+/3)
(см). Определить потенциальную и
кинетическую энергии тела в конце 1-ой
секунды движения.
(Ответ EMBED Equation.3
![]() ).
).
2.198. Уравнение колебаний материальной точки массой m=16г имеет вид X=2sin(t/8+/4) (см), где X выражается в сантиметрах. Определить кинетическую, потенциальную и полную энергию точки через 2 секунды после начала колебаний.
( Ответ: EMBED Equation.3
![]() ).
).
2.199.
Материальная точка массой 0,05 кг колеблется
по закону X=0,1sin(t/5+/3)(м).
Найти максимальную силу, действующую
на точку. (Ответ: EMBED Equation.3
![]() ).
).
2.200.В
результате значительной потери крови
содержание железа в ней уменьшилось на
210 мг. Недостаток железа EMBED Equation.3
вследствие его восстановления с течением
времени EMBED Equation.3
уменьшается по закону EMBED Equation.3
![]() (время выражено в сутках). Найти зависимость
скорости восстановления железа в крови
от времени. Вычислить эту скорость в
момент EMBED Equation.3
=0
и через 7 суток. (Ответ: EMBED Equation.3
(время выражено в сутках). Найти зависимость
скорости восстановления железа в крови
от времени. Вычислить эту скорость в
момент EMBED Equation.3
=0
и через 7 суток. (Ответ: EMBED Equation.3
 ;
EMBED Equation.3
;
EMBED Equation.3
![]() ).
).
2.201.
Фабричная труба выбрасывает за единицу
времени некоторое количество P
газообразного вещества, которое в
результате диффузии распространяется
в окружающем воздухе. Концентрация
этого вещества на расстоянии EMBED
Equation.3
![]() от отверстия трубы определяется формулой
EMBED Equation.3
от отверстия трубы определяется формулой
EMBED Equation.3
![]() ,
где EMBED Equation.3
,
где EMBED Equation.3
![]() -
коэффициент диффузии. Найти убывание
концентрации на каждую единицу расстояния
(градиент концентрации).
-
коэффициент диффузии. Найти убывание
концентрации на каждую единицу расстояния
(градиент концентрации).
(Ответ:
EMBED Equation.3
![]() ).
).
2.202.
Зависимость барометрического давления
от высоты при условии постоянной
температуры дается барометрической
формулой EMBED Equation.3
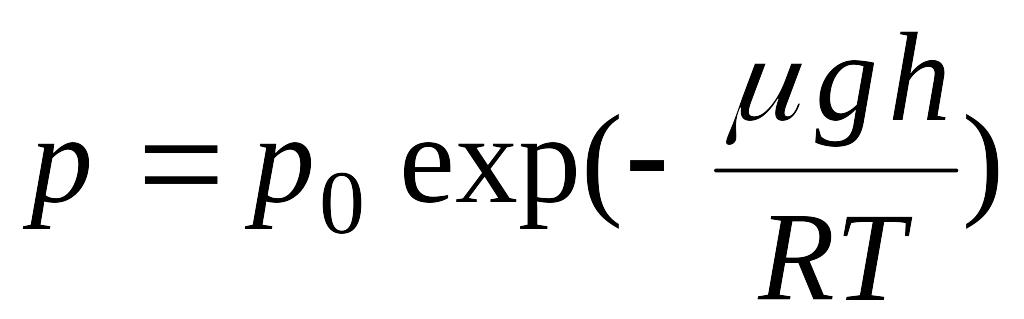 ,
где EMBED Equation.3
,
где EMBED Equation.3
![]() - давление на поверхности Земли (h=0),
EMBED Equation.3
- давление на поверхности Земли (h=0),
EMBED Equation.3
![]() - масса киломоля воздуха, EMBED Equation.3
- масса киломоля воздуха, EMBED Equation.3
![]() - универсальная газовая постоянная, Т
– абсолютная температура, EMBED Equation.3
- универсальная газовая постоянная, Т
– абсолютная температура, EMBED Equation.3
![]() - ускорение свободного падения.
- ускорение свободного падения.
Получить
формулу для определения градиента
давления (т.е. изменения атмосферного
давления на каждую единицу изменения
высоты) для любой высоты, считая
Т и EMBED
Equation.3
постоянными. (Ответ: EMBED Equation.3
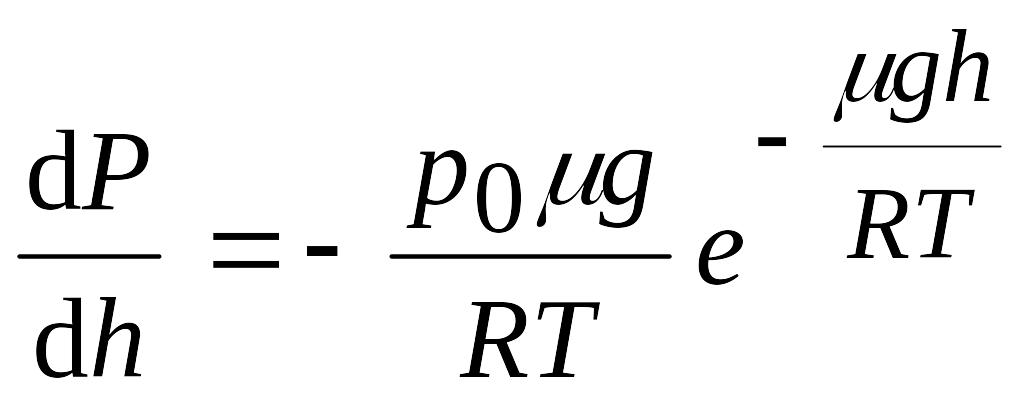 ).
).
2.203.
Концентрация раствора меняется с
течением времени по закону EMBED Equation.3
![]() ,
где EMBED Equation.3
,
где EMBED Equation.3
![]() и EMBED Equation.3
и EMBED Equation.3
![]() - постоянные для данного процесса
величины. Найти скорость растворения.
(Ответ: EMBED Equation.3
- постоянные для данного процесса
величины. Найти скорость растворения.
(Ответ: EMBED Equation.3
![]() ).
).
2.204.
Величина потенциала, возникающего при
возбуждении сетчатки глаза под действием
света, равна
EMBED Equation.3
![]() (В) ,
где EMBED Equation.3
(В) ,
где EMBED Equation.3
![]() - постоянная величина,
EMBED Equation.3
-
время, отсчитываемое от момента освещения.
Определить потенциал и скорость изменения
потенциала в момент времени EMBED Equation.3
=0.
(Ответ: EMBED Equation.3
- постоянная величина,
EMBED Equation.3
-
время, отсчитываемое от момента освещения.
Определить потенциал и скорость изменения
потенциала в момент времени EMBED Equation.3
=0.
(Ответ: EMBED Equation.3
![]() скорость изменения потенциала EMBED
Equation.3
скорость изменения потенциала EMBED
Equation.3
![]() (В/с)).
(В/с)).
2.205.
Конденсатор емкостью С
и зарядом
EMBED Equation.3
![]() разряжается через сопротивление R
так, что в любой момент времени EMBED
Equation.3
заряд EMBED Equation.3
разряжается через сопротивление R
так, что в любой момент времени EMBED
Equation.3
заряд EMBED Equation.3
![]() меняется по закону EMBED Equation.3
меняется по закону EMBED Equation.3
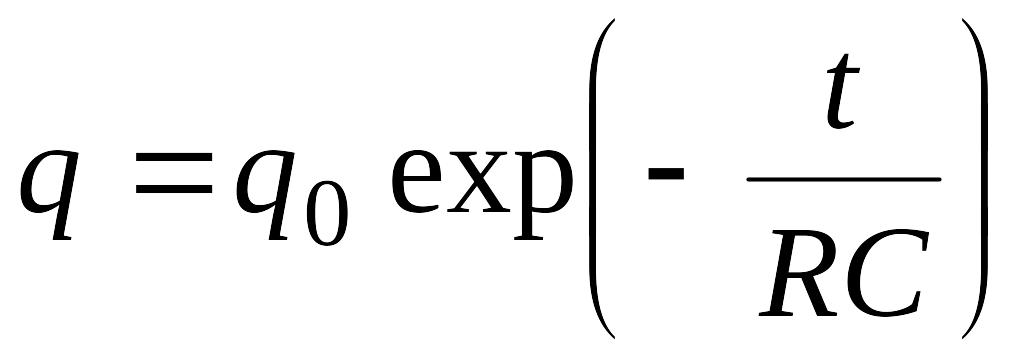 .
Найти скорость изменения заряда
конденсатора. Какова величина этой
скорости в начале разряда ( EMBED Equation.3
=0)?
Какой физический смысл имеет скорость
изменения заряда? (Ответ: EMBED
Equation.3
.
Найти скорость изменения заряда
конденсатора. Какова величина этой
скорости в начале разряда ( EMBED Equation.3
=0)?
Какой физический смысл имеет скорость
изменения заряда? (Ответ: EMBED
Equation.3
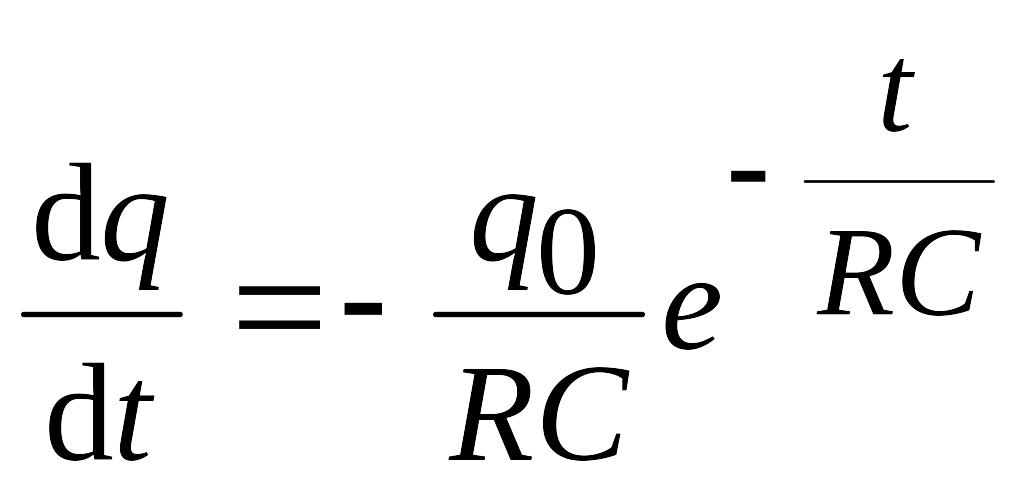 ;
EMBED Equation.3
;
EMBED Equation.3
![]() ).
).
2.206
. На бактерии действуют ультрафиолетовым
излучением Доля убитых бактерий (в
процентах) в зависимости от времени
действия излучения описывается
приближенной формулой EMBED Equation.3
![]() ,
где EMBED Equation.3
- постоянная величина, определяемая
видом бактерий и условиями воздействия.
Получите формулу для расчета доли
бактерий, уничтожаемых излучением при
данных условиях за единицу времени.
(Ответ: EMBED Equation.3
,
где EMBED Equation.3
- постоянная величина, определяемая
видом бактерий и условиями воздействия.
Получите формулу для расчета доли
бактерий, уничтожаемых излучением при
данных условиях за единицу времени.
(Ответ: EMBED Equation.3
![]() .
.
