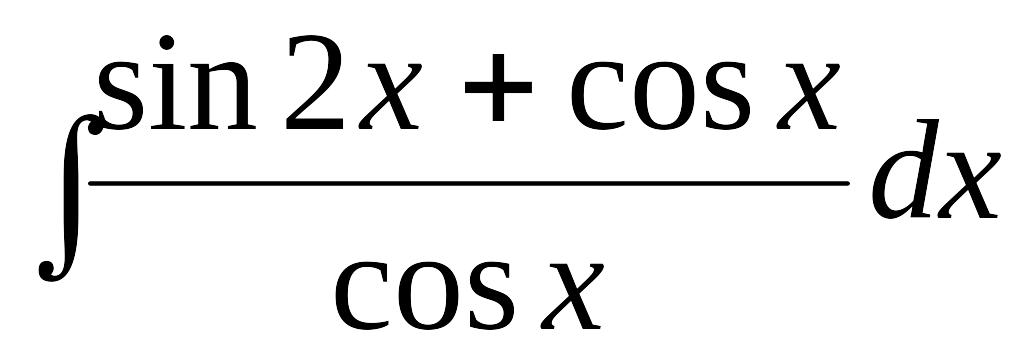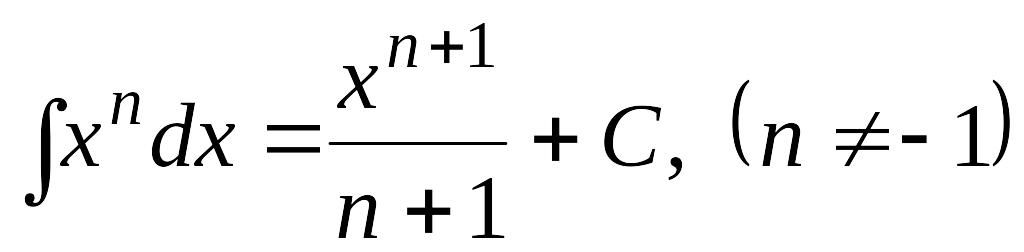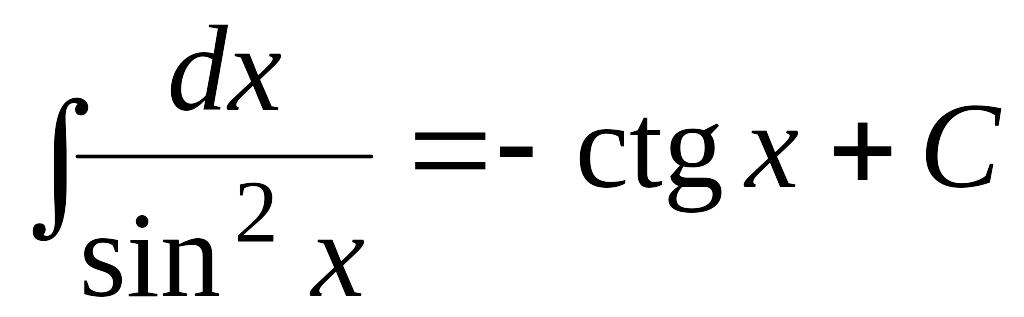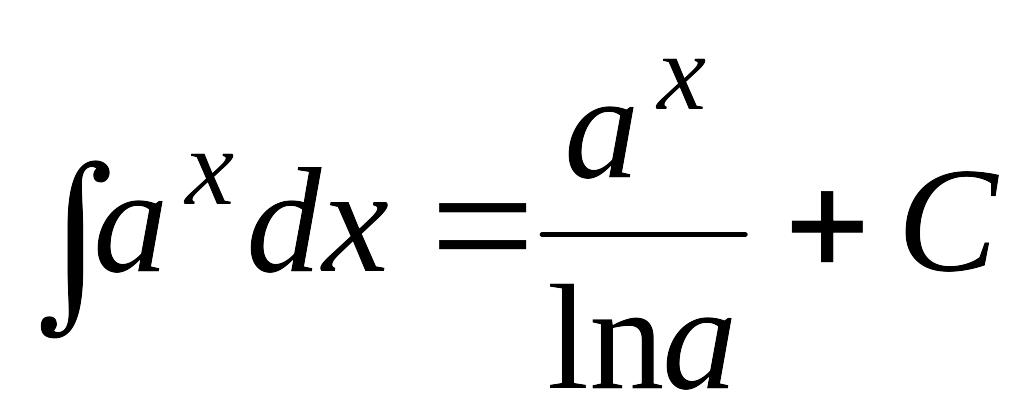Глава 4 неопределенный интеграл4
§1. Непосредственное интегрирование.
Функция
EMBED Equation.3
называется первообразной
для функции
EMBED Equation.3
,
если
EMBED
Equation.3
или
EMBED
Equation.3
.
Любая непрерывная функция EMBED Equation.3 имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым С.
Совокупность
EMBED Equation.3
всех первообразных для функции EMBED
Equation.3
называется неопределенным
интегралом
от этой функции:
Основные свойства неопределенного интеграла
EMBED Equation.3
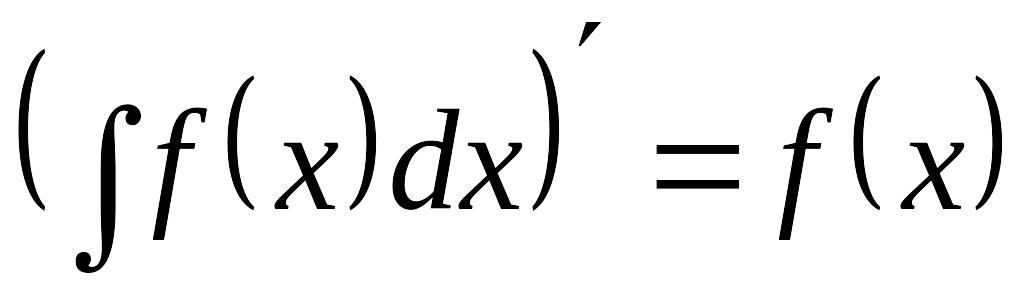или EMBED Equation.3
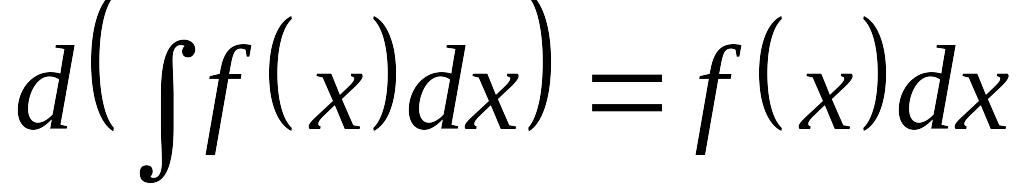
EMBED Equation.3
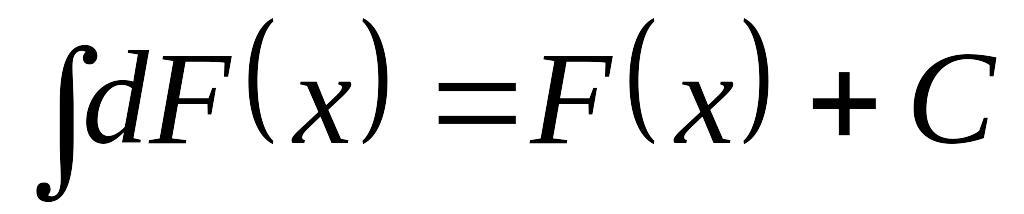
EMBED Equation.3
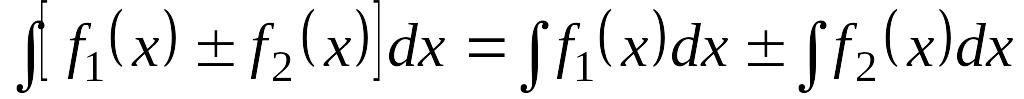
EMBED Equation.3
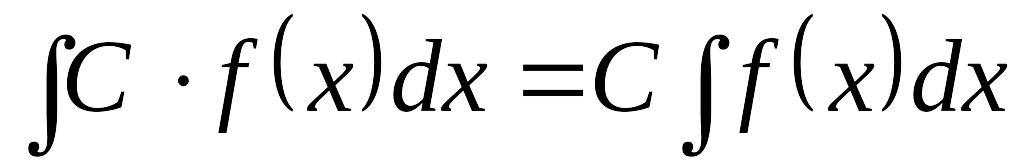
Таблица простейших интегралов
|
|||
1. |
EMBED
Equation.3
|
7. |
EMBED
Equation.3
|
2. |
EMBED
Equation.3
|
8. |
EMBED
Equation.3
|
3. |
EMBED
Equation.3
|
9. |
EMBED
Equation.3
|
4. |
EMBED
Equation.3
|
10.
|
EMBED
Equation.3
|
5. |
EMBED
Equation.3
|
11. |
EMBED
Equation.3
|
6. |
EMBED
Equation.3
|
12.
|
EMBED
Equation.3
|
Проинтегрировать функцию EMBED Equation.3 значит найти её неопределенный интеграл. Непосредственное интегрирование основано на прямом использовании основных свойств неопределенного интеграла и таблицы простейших интегралов.
Рассмотрим следующие примеры:
1). Найти интеграл
EMBED
Equation.3
.
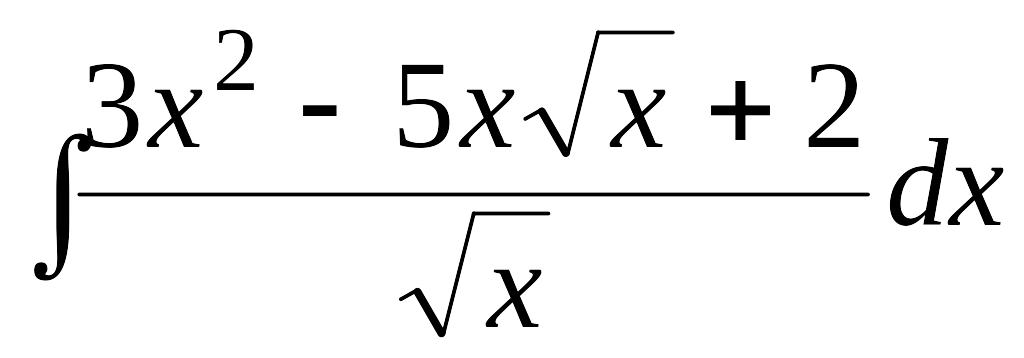Разделив почленно числитель на знаменатель, разложим подынтегральную функцию на слагаемые, после чего проинтегрируем каждое из полученных выражений:
EMBED
Equation.3
Через С обозначен результат суммирования всех произвольных постоянных, получающихся при интегрировании каждого слагаемого.
2). Вычислить интеграл
EMBED
Equation.3
Представим подынтегральную функцию следующим образом:
EMBED
Equation.3
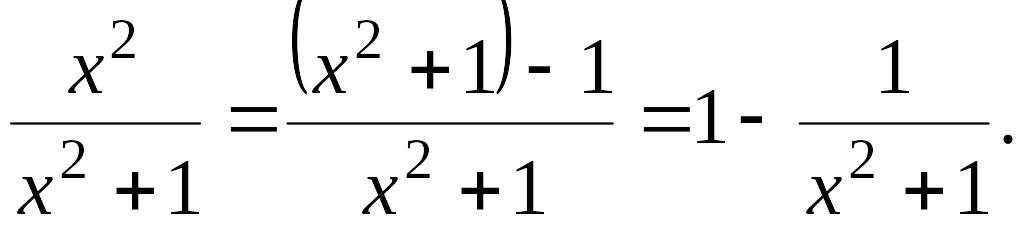
Тогда
EMBED
Equation.3
3). Найти интеграл
EMBED
Equation.3
Представим подынтегральную функцию в таком виде:
EMBED
Equation.3
Подставим полученное выражение :
EMBED
Equation.3
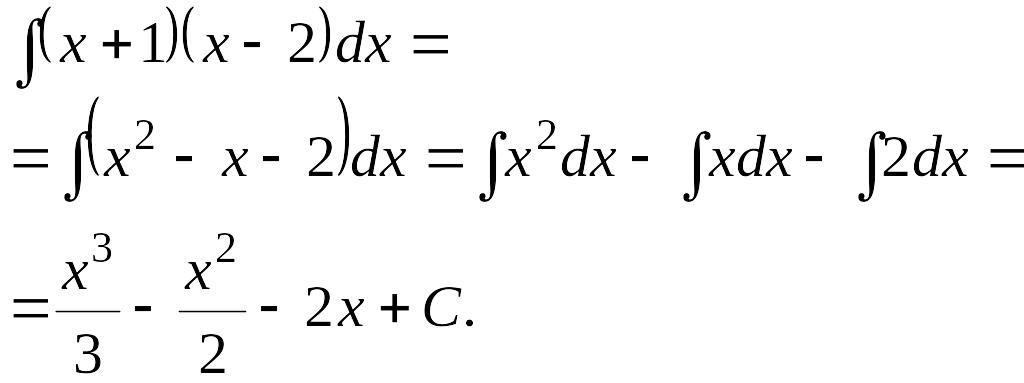
4). Вычислить интеграл
EMBED
Equation.3
Преобразуем подынтегральную функцию таким образом:
EMBED
Equation.3
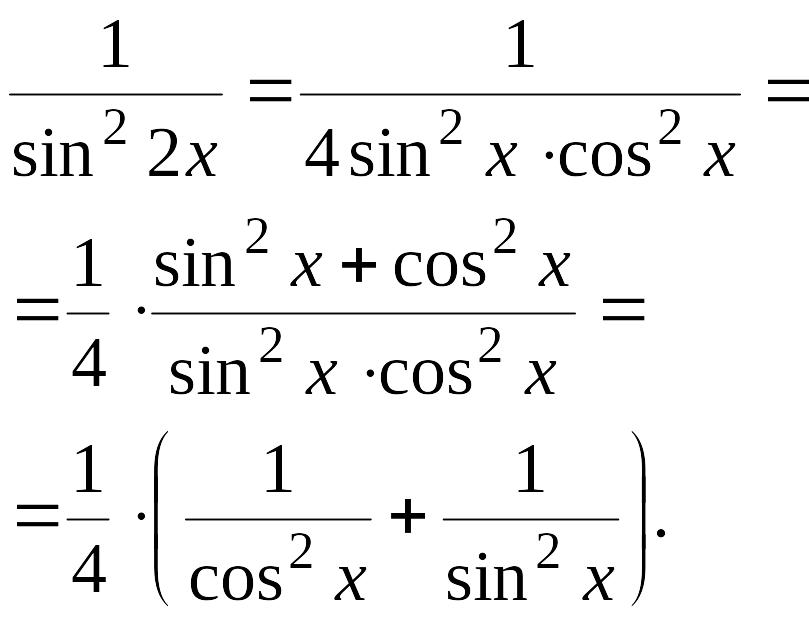
Подставляя полученную функцию, вычисляем интеграл:
EMBED
Equation.3
Используя правила интегрирования и таблицу интегралов найти следующие интегралы:
-
EMBED Equation.3
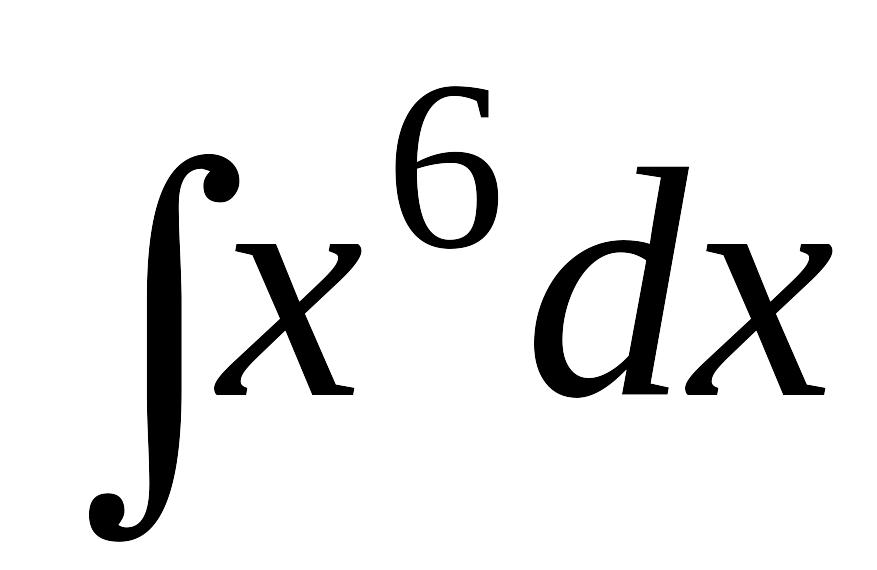
EMBED Equation.3
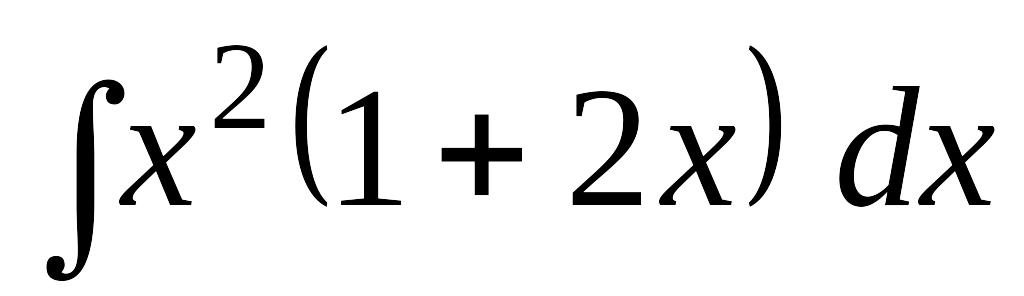
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
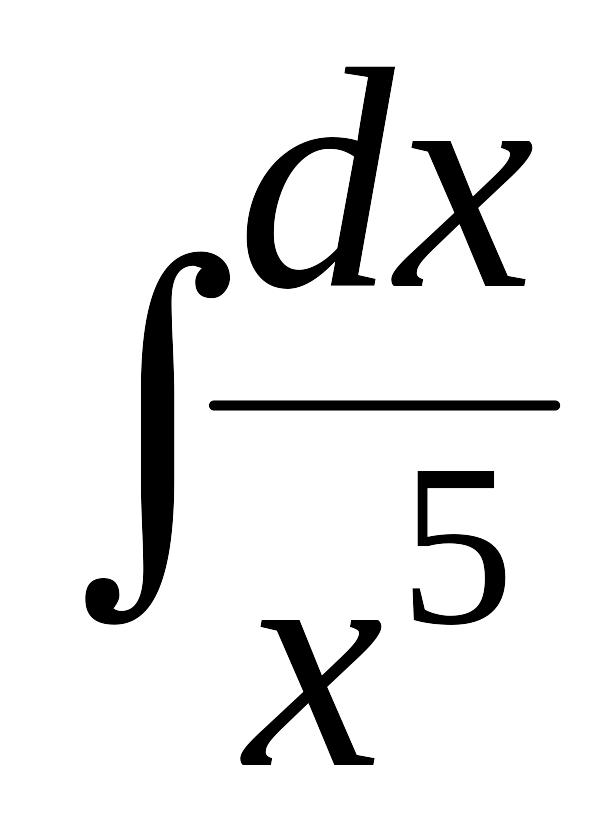
EMBED Equation.3
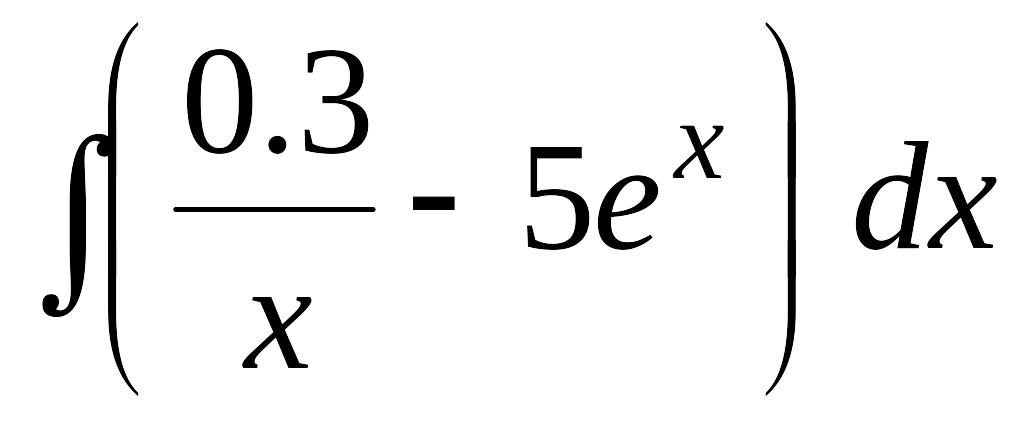
EMBED Equation.3
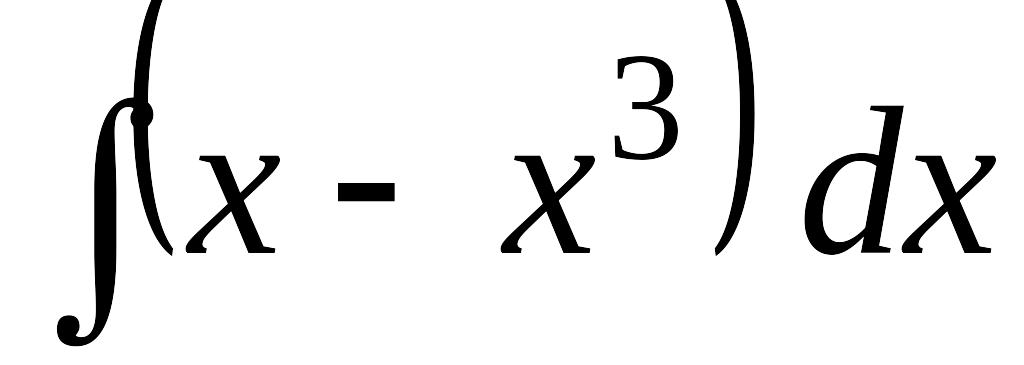
EMBED Equation.3
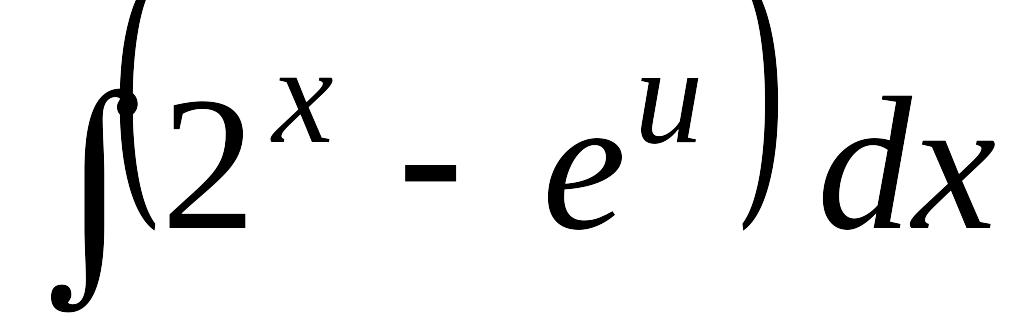
EMBED Equation.3
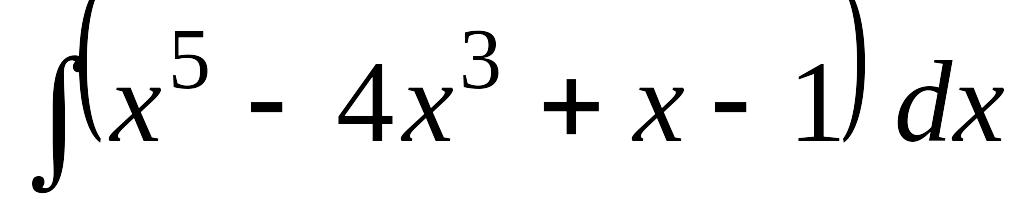
EMBED Equation.3
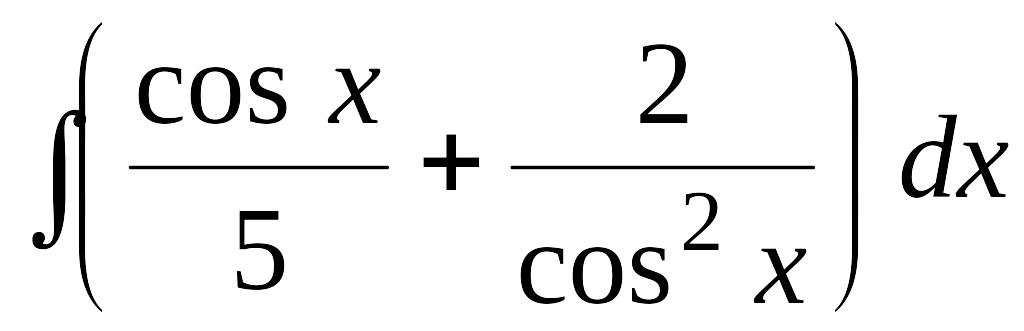
EMBED Equation.3
EMBED Equation.3
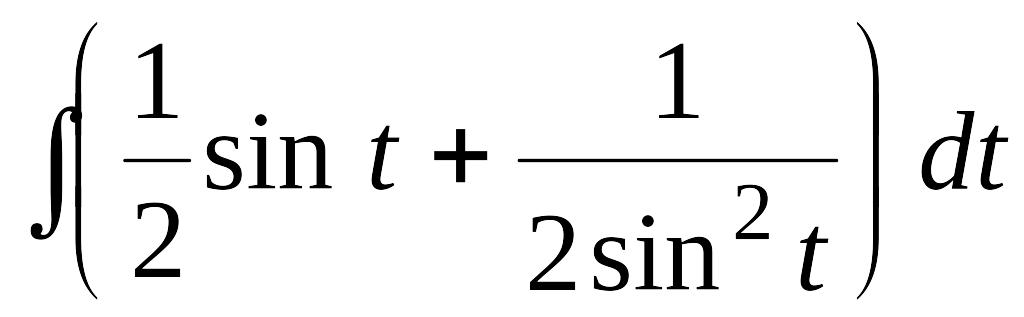
EMBED Equation.3
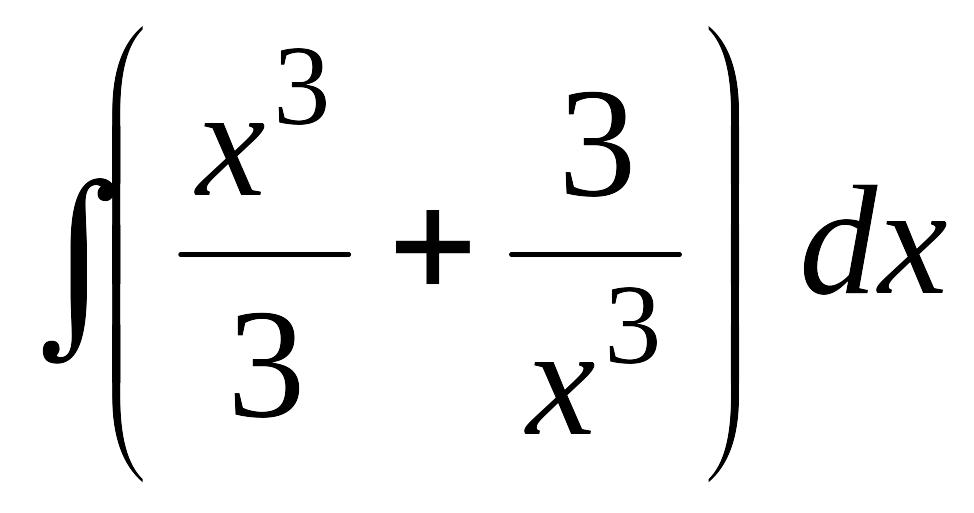
EMBED Equation.3
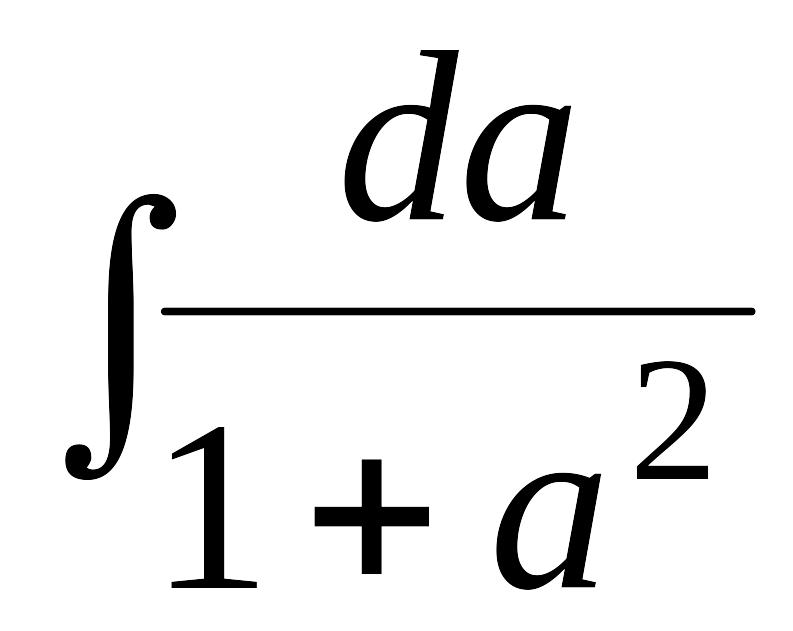
EMBED Equation.3
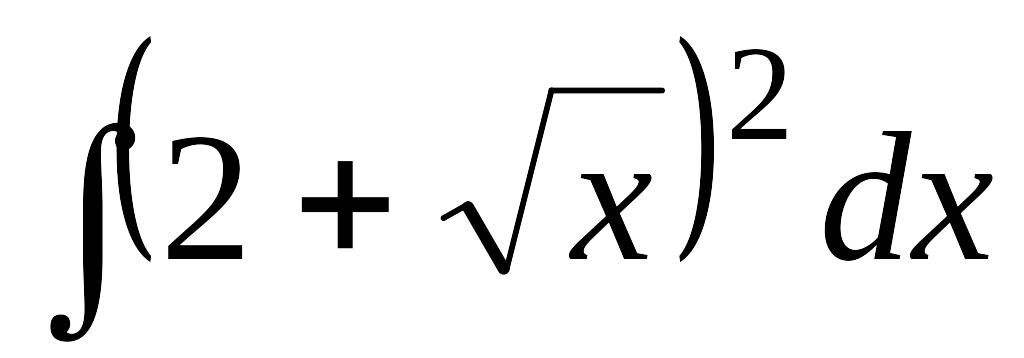
EMBED Equation.3
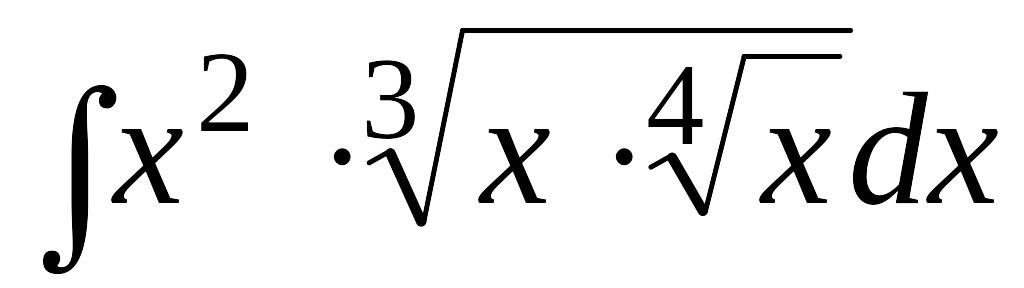
EMBED Equation.3
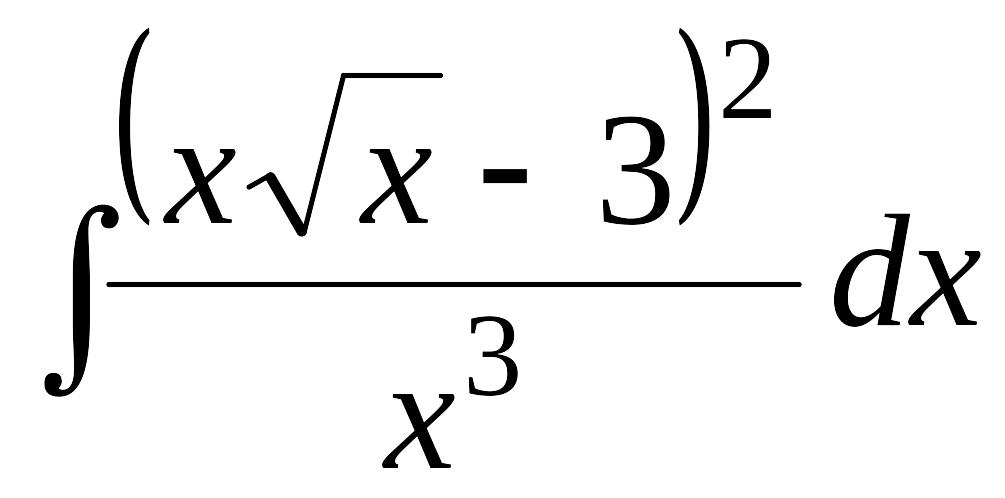
EMBED Equation.3
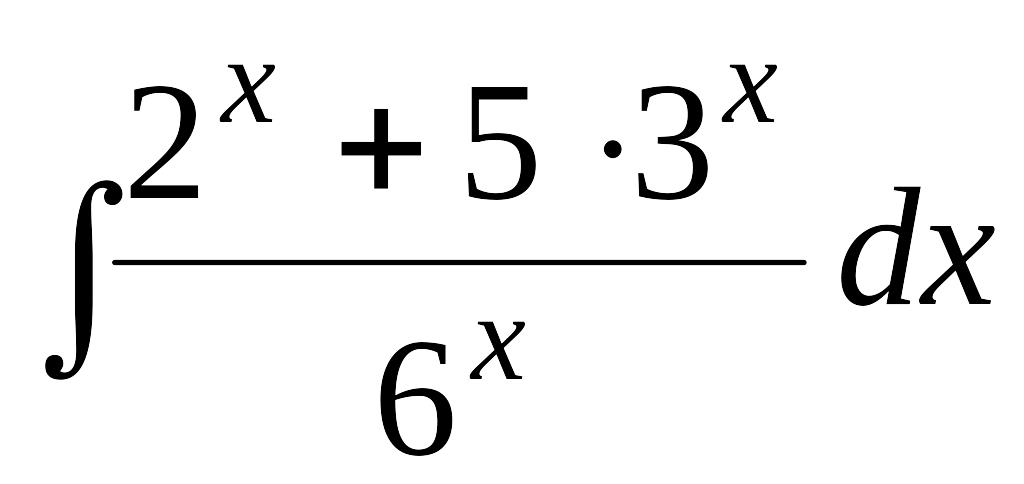
EMBED Equation.3
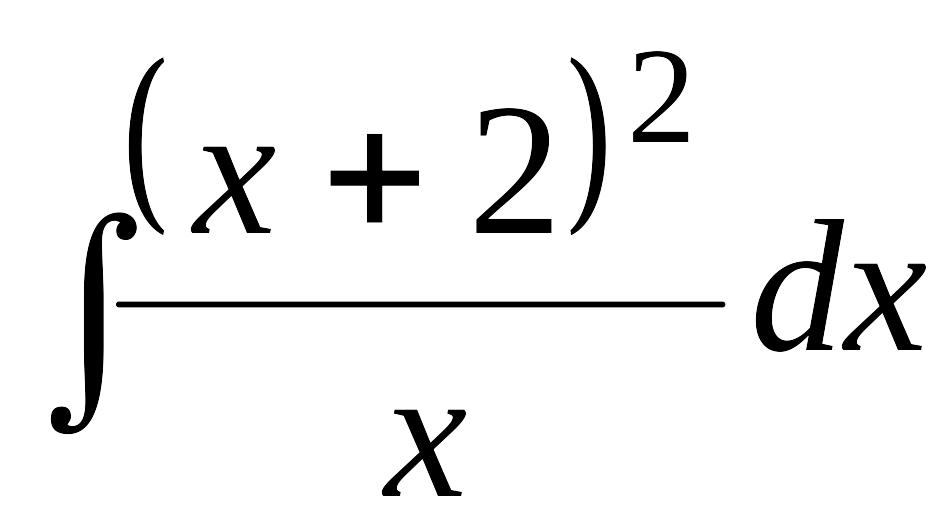
EMBED Equation.3
