§4. Производные высших порядков
Производная
второго порядка (вторая производная)
от функции EMBED Equation.3
есть производная от ее производной,
т.е.
EMBED
Equation.3
.
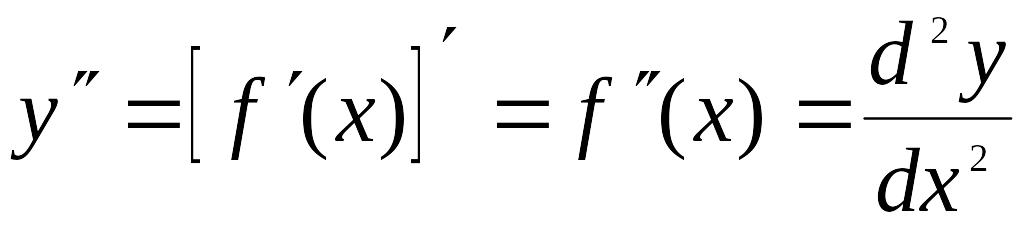Производная третьего порядка (третья производная) от функции EMBED Equation.3 есть производная от ее второй производной:
EMBED
Equation.3
Вообще производная n-го порядка ( n-я производная) функции EMBED Equation.3 есть производная от ее (n-1)-й производной.
Рассмотрим пример.
Найти
третью производную от функции EMBED
Equation.3
.
Дифференцируя
данную функцию, получим
EMBED Equation.3
.
Дифференцируя производную EMBED Equation.3
,
найдем: EMBED Equation.3
.
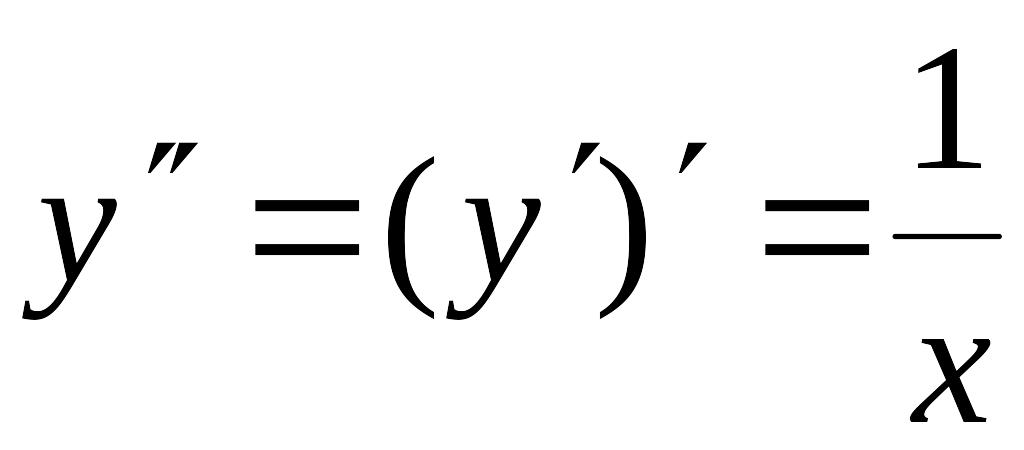Отсюда третья производная EMBED Equation.3
.
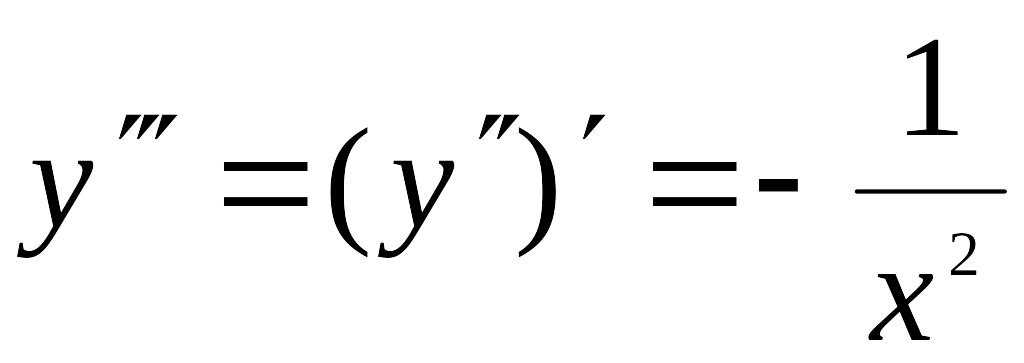Найти производные второго порядка от функций:
2.127. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
2.128 |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
|
2.129. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
2.130. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
|
2.131. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
2.132. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
|
2.133. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
2.134 |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
|
)
)
)
)
)
)
)
)
Найти производные третьего порядка от функций:
2.135. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
2.136. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
2.137. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
2.138. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
2.139. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
2.140. |
EMBED
Equation.3
(Ответ:
EMBED Equation.3
|
)
)
)
)
)
)§5. Дифференциал функции
Дифференциалом
(первого порядка) функции EMBED Equation.3
называется главная часть ее приращения,
линейная относительно приращения
аргумента.
Дифференциалом
аргумента называется приращение этого
аргумента: EMBED Equation.3
Дифференциал функции равен произведению ее производной на дифференциал аргумента:
EMBED
Equation.3
Основные свойства дифференциала.
1.
EMBED Equation.3
,
где С=const
2.
EMBED Equation.3
3.
EMBED Equation.3
4.
EMBED Equation.3
5.
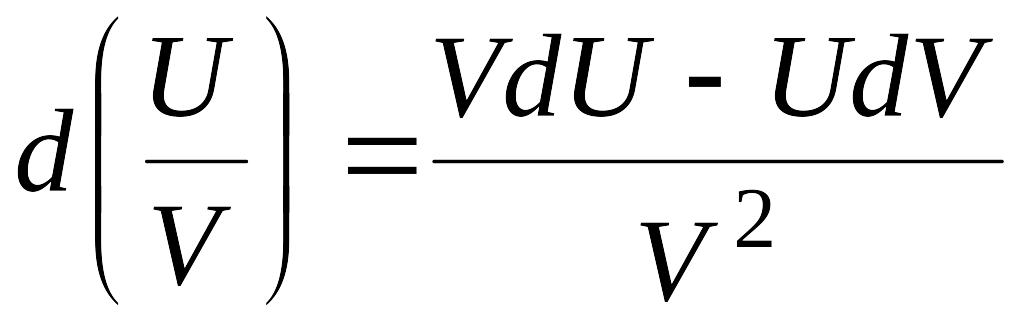EMBED Equation.3
,
EMBED Equation.3
6.
EMBED Equation.3
Если
приращение аргумента EMBED Equation.3
мало по абсолютной величине, то EMBED
Equation.3
и EMBED Equation.3
.
Полученное выражение позволяет
использовать дифференциал функции для
приближенных вычислений.
Дифференциалом
второго порядка функции EMBED Equation.3
называется
дифференциал от дифференциала первого
порядка: EMBED Equation.3
.
Аналогично определяется дифференциал
третьего и более высоких порядков.
Используя определение дифференциала, рассмотрим ряд примеров.
Найти приращение EMBED Equation.3
и дифференциал EMBED Equation.3
функции EMBED Equation.3
при EMBED Equation.3
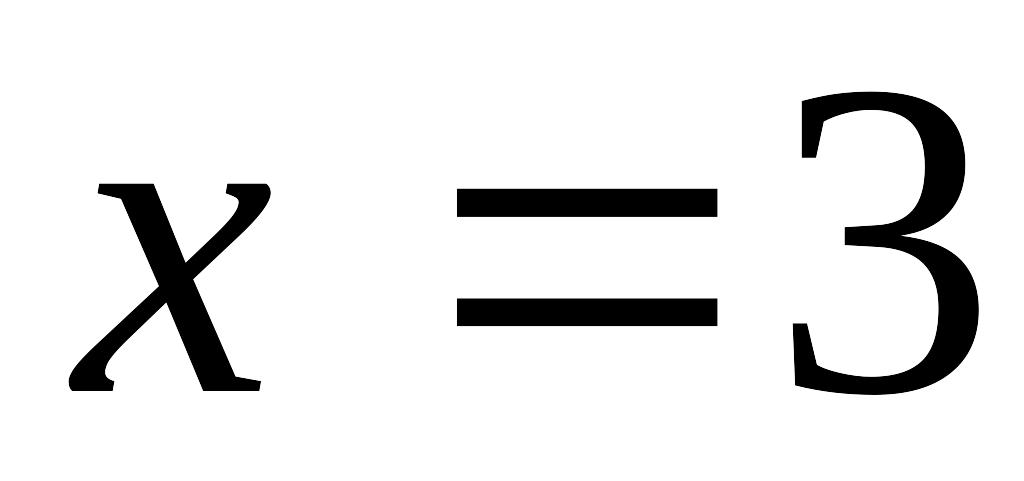и EMBED Equation.3
=0,01.
Каковы абсолютная и относительная
погрешности, которые допускаются при
замене приращения функции ее
дифференциалом?
Имеем
EMBED
Equation.3
=
EMBED Equation.3
EMBED Equation.3
.
Найдем дифференциал функции:
EMBED
Equation.3
.
Абсолютная погрешность
EMBED
Equation.3
.
Относительная погрешность
EMBED
Equation.3
.
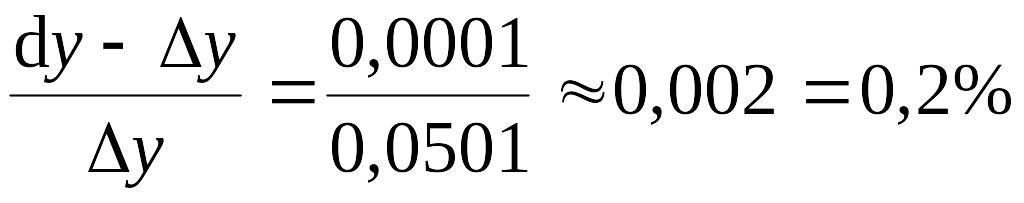Найти дифференциалы первого и второго порядков функции EMBED Equation.3
.
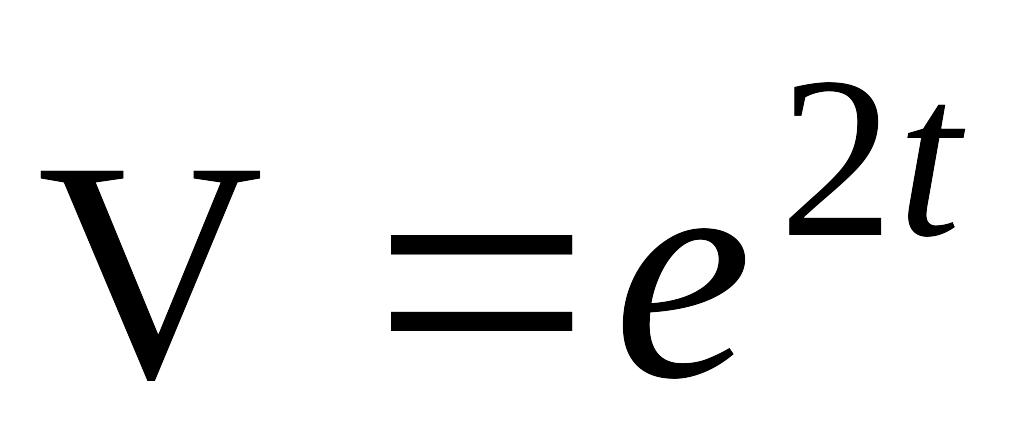Имеем
EMBED
Equation.3
- дифференциал первого порядка,
EMBED
Equation.3
- дифференциал второго порядка.
Вычислить приближенное значение EMBED Equation.3
.
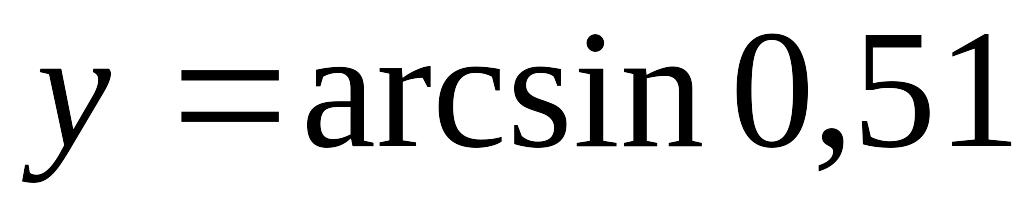Рассмотрим
функцию EMBED Equation.3
.
Полагая EMBED Equation.3
,
EMBED Equation.3
и применяя формулу EMBED Equation.3
,
получаем
EMBED
Equation.3
.
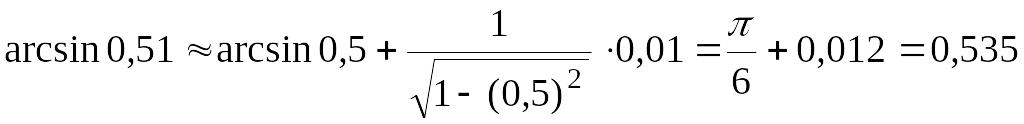Вычислить приближенное значение площади круга, радиус которого равен 3,02 м.
Воспользуемся
формулой EMBED Equation.3
.
Полагая R=3,
EMBED Equation.3
,
имеем
EMBED
Equation.3
.
Следовательно, площадь круга радиуса 3,02м имеет приближенное значение
EMBED
Equation.3
.
Вычислить приближенно EMBED Equation.3
.
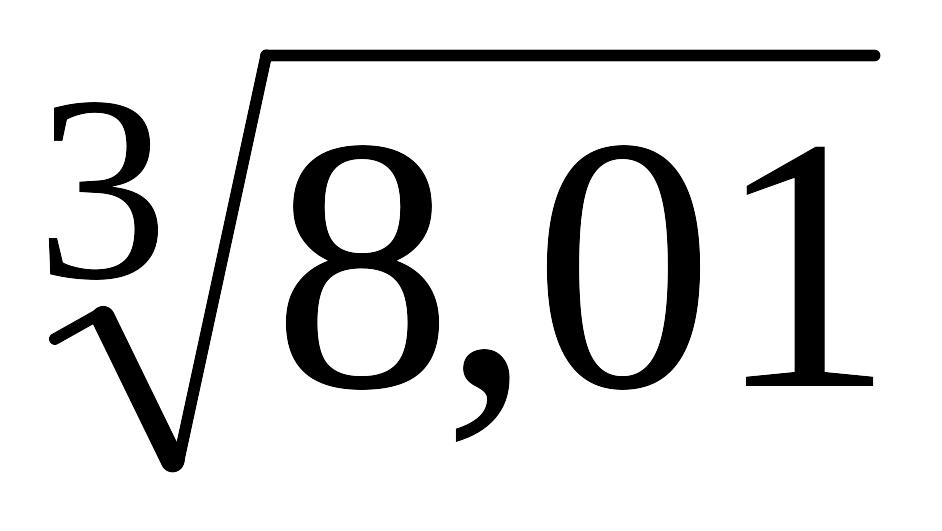Рассмотрим
функцию EMBED Equation.3
и положим x=8,
EMBED Equation.3
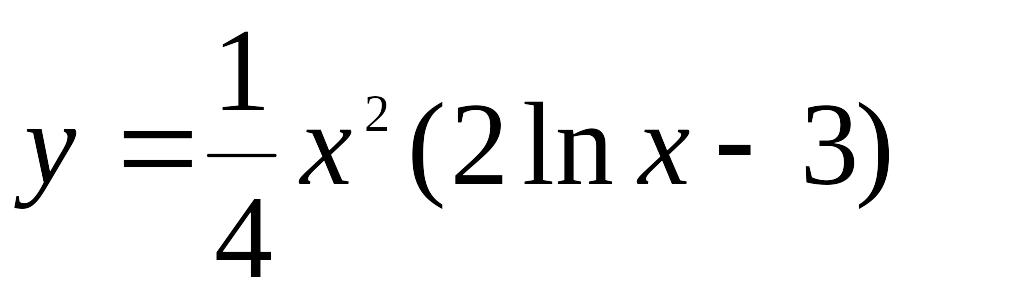
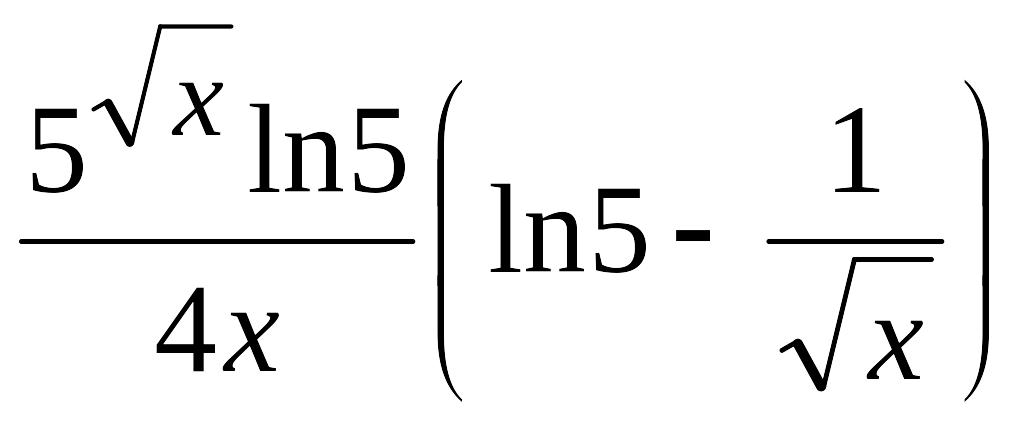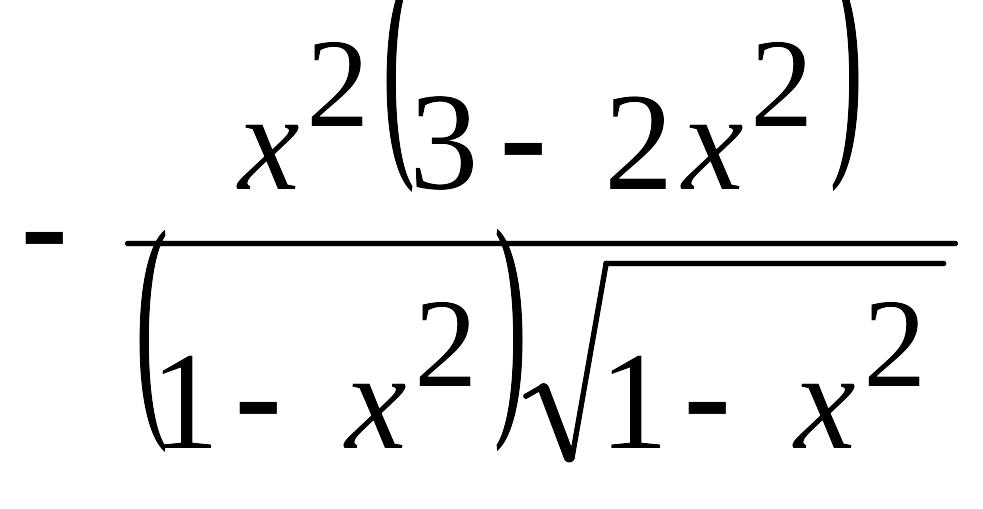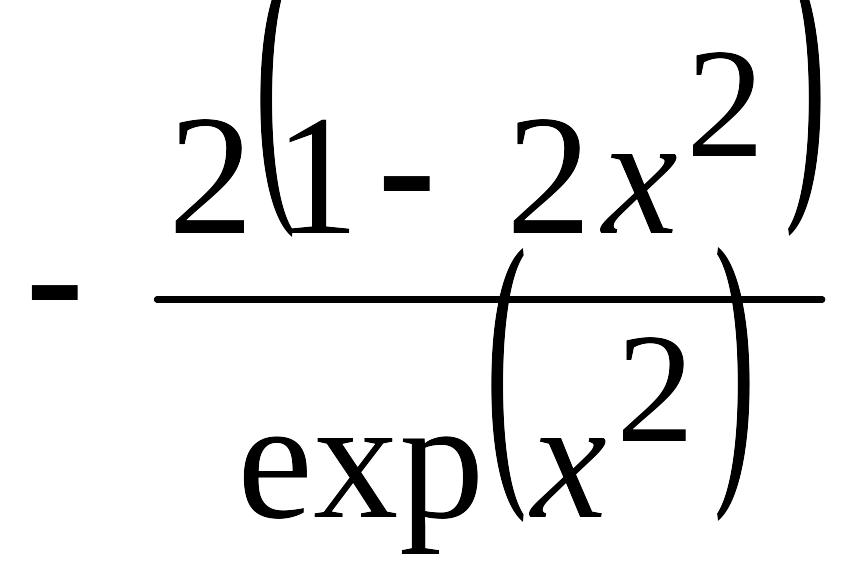