Файловый архив студентов. Файловый архив студентов.
1301 вуз, 5079 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Пермский государственный медицинский университет им. ак. Е.А. Вагнера
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
Исправленный вариант математика.doc
Скачиваний:
22
Добавлен:
09.11.2019
Размер:
13.23 Mб
Скачать
☆
►Содержание►

Глава 2 дифференциальное исчисление функций одной независимой переменной

§ 1. Понятие производной

Пусть и - два значения аргумента, а и - соответствующие значения функции . Тогда разность называется приращением аргумента, а разность = - приращением функции на отрезке .

Производной от функции по аргументу называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

или

Примечание.

Производная обозначается также как (Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по .

Отыскание производной называется дифференцированием функции.

Исходя из определения производной, можно найти производную любой дифференцируемой функции.

Рассмотрим несколько примеров.

1. Найти производную функции

(1)

Дадим приращение , тогда получит приращение :

,

отсюда

.

Функция задается формулой (1). Тогда

=

=

Находим отношение приращения функции к приращению аргумента:

= .

Найдем предел этого отношения при :

= ( )=

Следовательно, по определению производной

2. Найти производную функции

(2)

Находим приращение функции отсюда

= и

=

Таким образом,

Итак,

3. Найти производную функции

(3)

Находим приращение функции

Воспользуемся формулой

Отсюда

и

= .

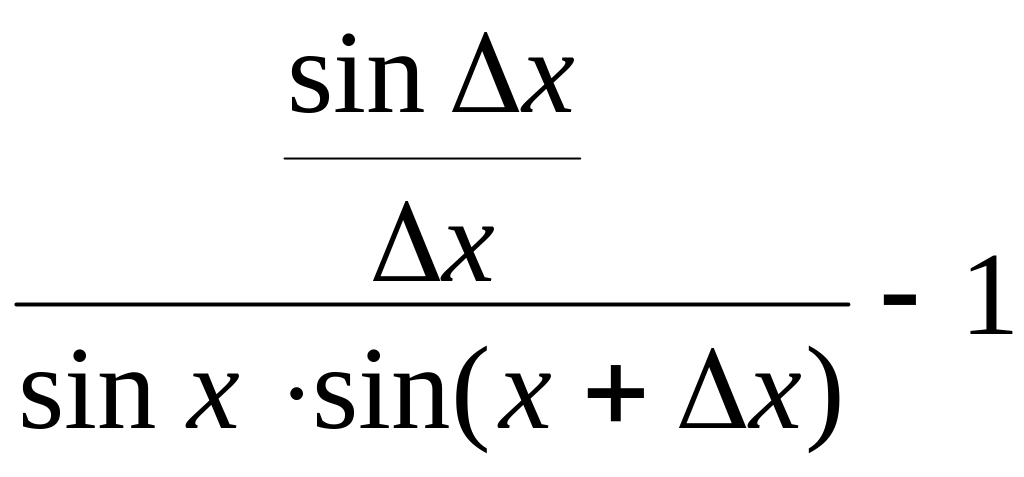Итак,

=

Исходя из определения производной, найти производные следующих функций:

2.1. (Ответ:  )

2.5. (Ответ: )

2.2. (Ответ: )

2.6. . (Ответ: )

2.3.

(Ответ: )

2.7. .

(Ответ: )

2.4.

Ответ: )

2.8. .

(Ответ: 6(x1))

§2. Основные правила дифференцирования.

Дифференцирование основных элементарных функций.

Основные правила дифференцирования

Пусть C –постоянная, - функции, имеющие производные, тогда:

1.

2.

3.

4.

5.

Таблица производных

основных элементарных функций

1.

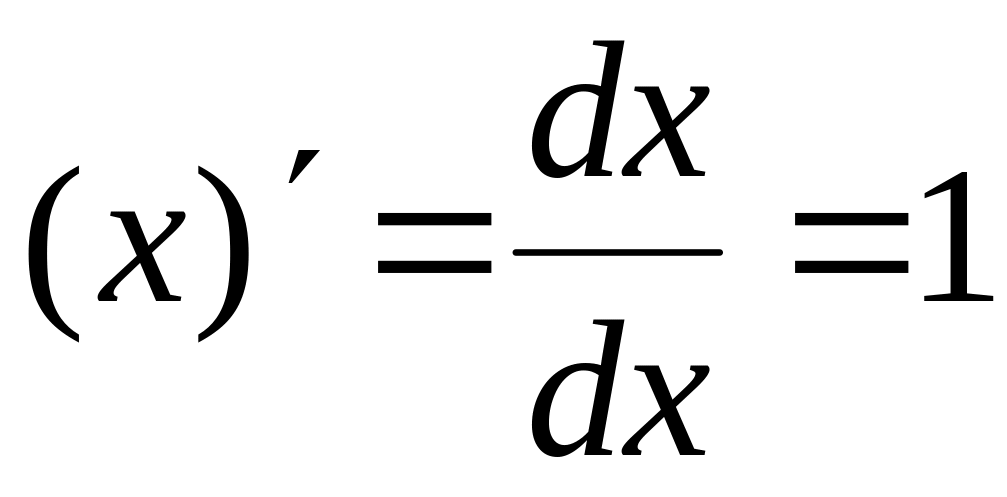
2.

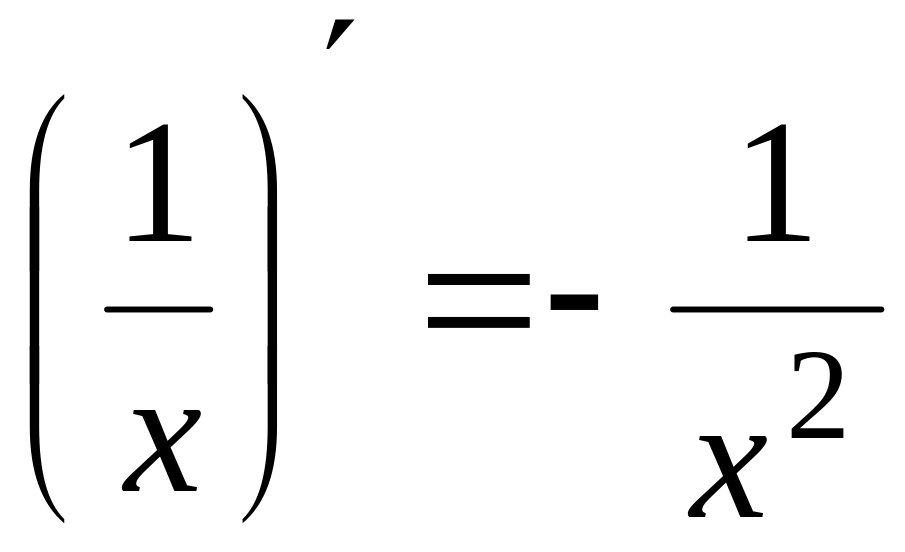
3.

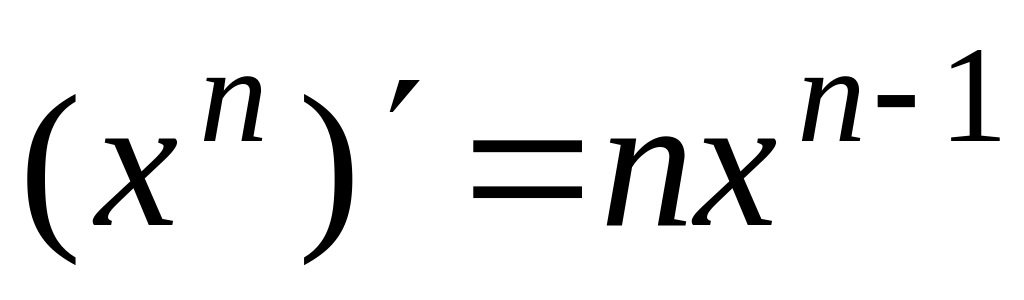
4.

5.

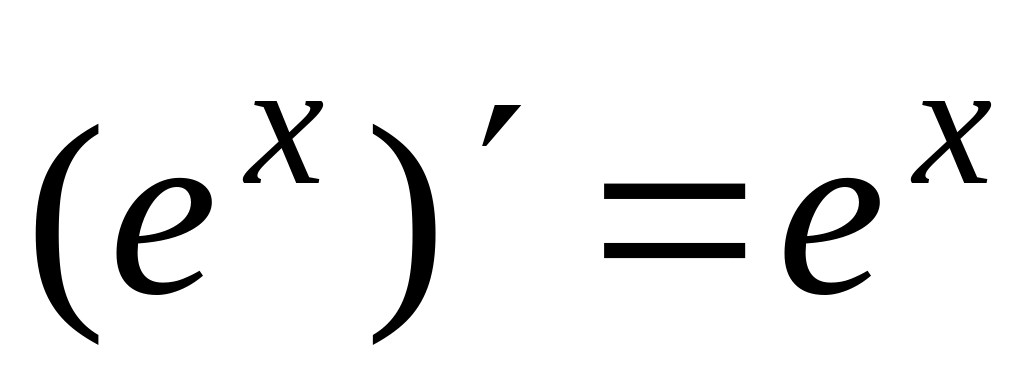
6.

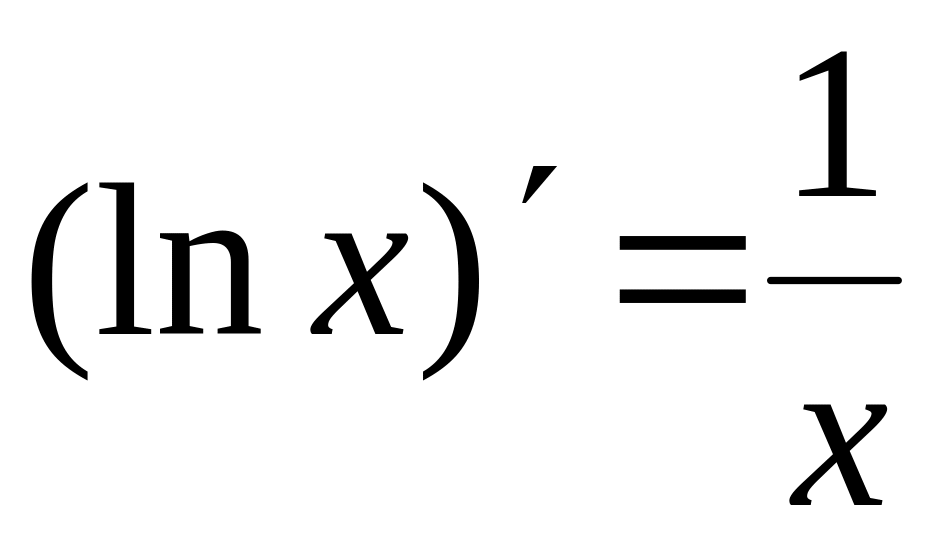
7.

8.

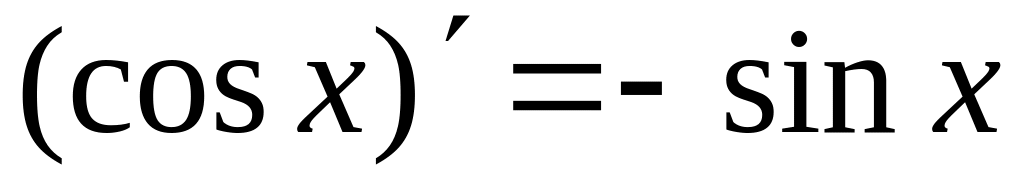
9.

10.

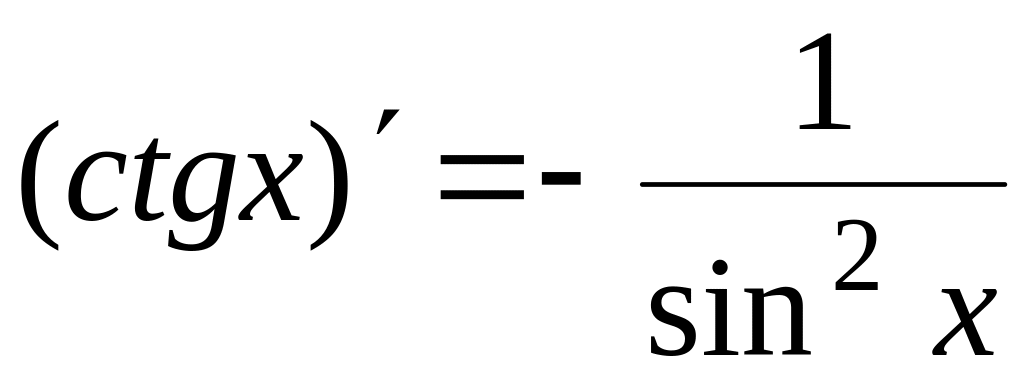
11.

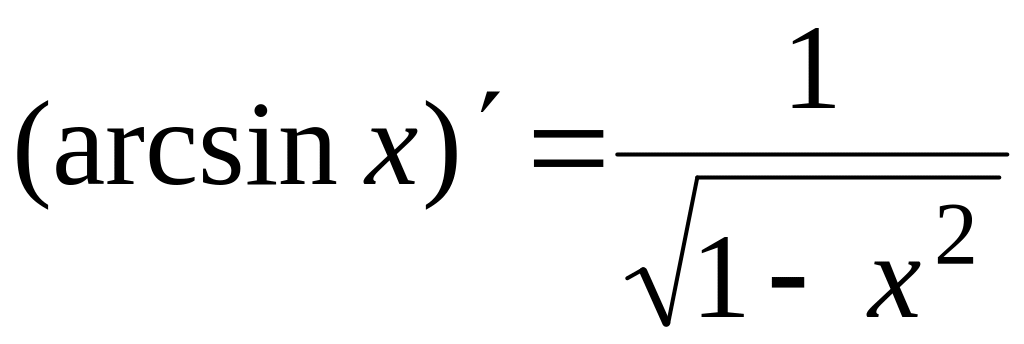
12.

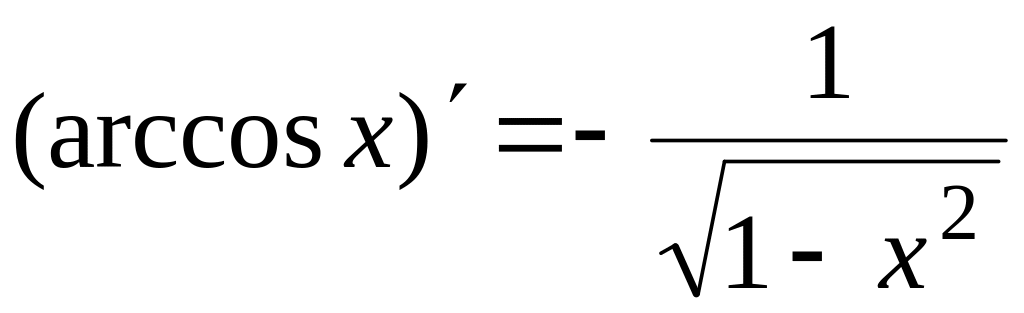
13.

14.

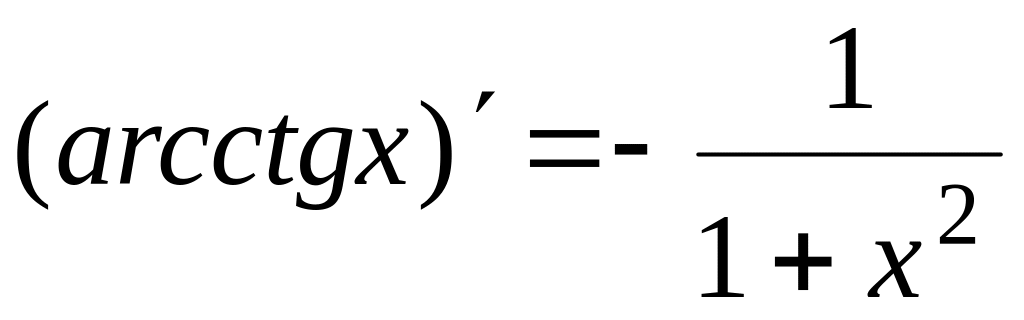
Применяя формулы и правила дифференцирования, найдем производную функции:

Запишем данную функцию следующим образом:

Тогда

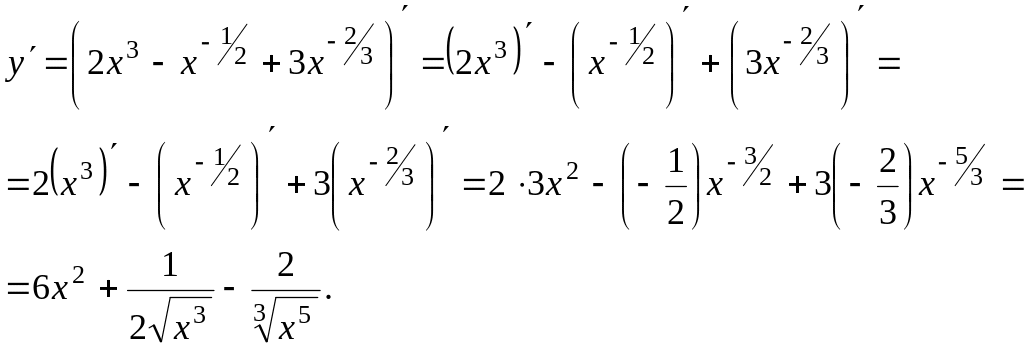
В качестве следующего примера найдем производную от функции

.

Для нахождения производной воспользуемся правилом нахождения производной от произведения двух функций:

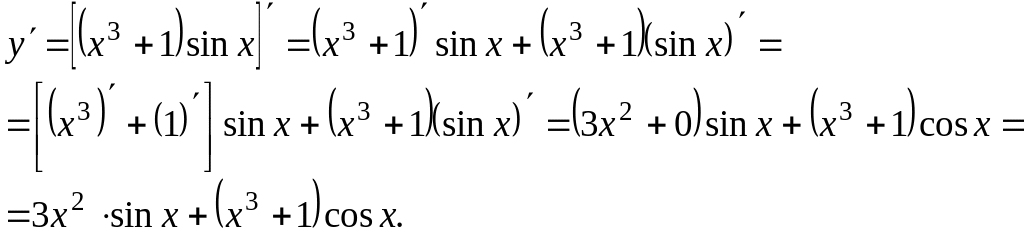
И, наконец, рассмотрим еще один пример: нахождение производной частного от деления двух функций

.

Для нахождения производной воспользуемся пятым правилом из раздела «Основные правила дифференцирования». Тогда

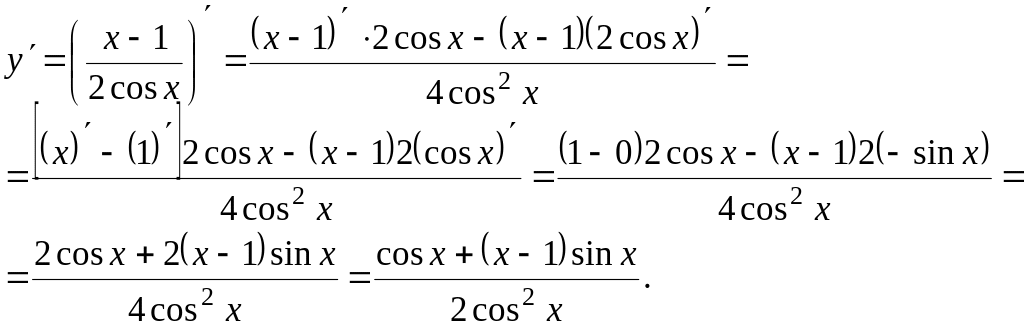
Найти производные следующих функций:

2.9.

§.

(Ответ: 6(x1))

2.10.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.11.

EMBED Equation.3 .

(Ответ: 2x(24x2+1))

2.12.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.13.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.14.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.15.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.16.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.17.

EMBED Equation.3 .

(Ответ: 4 EMBED Equation.3 EMBED Equation.3 )

2.18.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.19.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.20.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.21.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.22.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.23.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.24.

EMBED Equation.3

(Ответ: EMBED Equation.3 )

2.25.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.26. (Ответ:

EMBED Equation.3 .

( EMBED Equation.3 )

2.27. (Ответ:

EMBED Equation.3 .

( EMBED Equation.3 )

2.28.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.29.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.30.

EMBED Equation.3 .

(Ответ:  EMBED Equation.3 )

2.31.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.32.

(Ответ

EMBED Equation.3

EMBED Equation.3 )

2.33.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.34.

EMBED Equation.3 .

(Ответ:  EMBED Equation.3 )

2.35.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.36. (Ответ

EMBED Equation.3 .

EMBED Equation.3 )

2.37.

EMBED Equation.3 .

(Ответ: 0)

2.38.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.39.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.40.

EMBED Equation.3

(Ответ: EMBED Equation.3 )

2.41. (Ответ:

EMBED Equation.3 .

EMBED Equation.3 )

2.42. (Ответ

EMBED Equation.3 .

EMBED Equation.3

2.43. (Ответ

EMBED Equation.3 .

)

2.44.

EMBED Equation.3

(Ответ: EMBED Equation.3 )

2.45. (Ответ:

EMBED Equation.3 .

EMBED Equation.3 )

2.46.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.47.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.48.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.49.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.50.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.51.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.52.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.53.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.54.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.55.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.56.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.57.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.58.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.59.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.60.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.61.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.62.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.63.

EMBED Equation.3

(Ответ: EMBED Equation.3 )

2.64.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.65.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.66.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.67.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.68.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.69.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.70.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.71.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.72.

EMBED Equation.3

(Ответ: EMBED Equation.3 )

2.73.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.74.1

EMBED Equation.3

(Ответ: EMBED Equation.3 )

2.75.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.76.

EMBED Equation.3

(Ответ: EMBED Equation.3 )

2.77.

EMBED Equation.3 .

(Ответ: EMBED Equation.3 )

2.78.

EMBED Equation.3

(Ответ: EMBED Equation.3 )

2.79.2

EMBED Equation.3

(Ответ: EMBED Equation.3 )

2.80.3

EMBED Equation.3

(Ответ: EMBED Equation.3 )

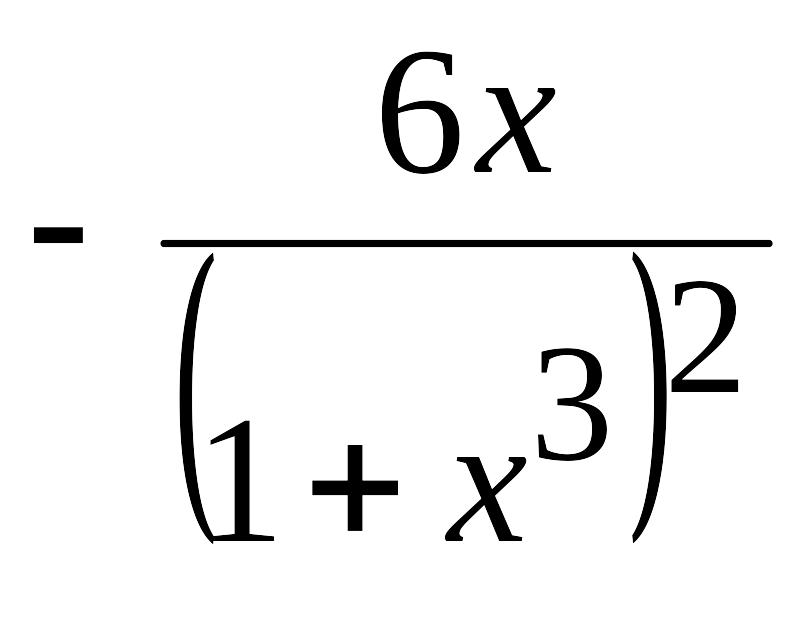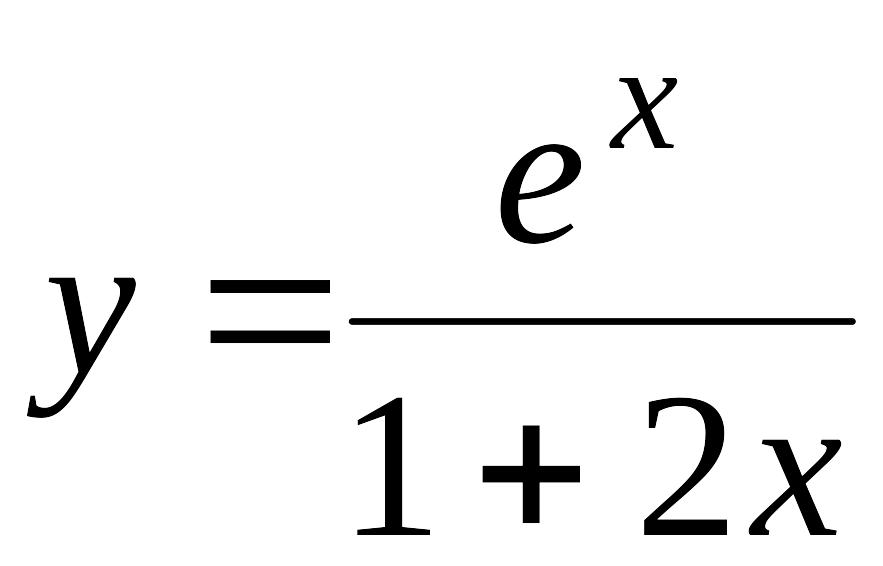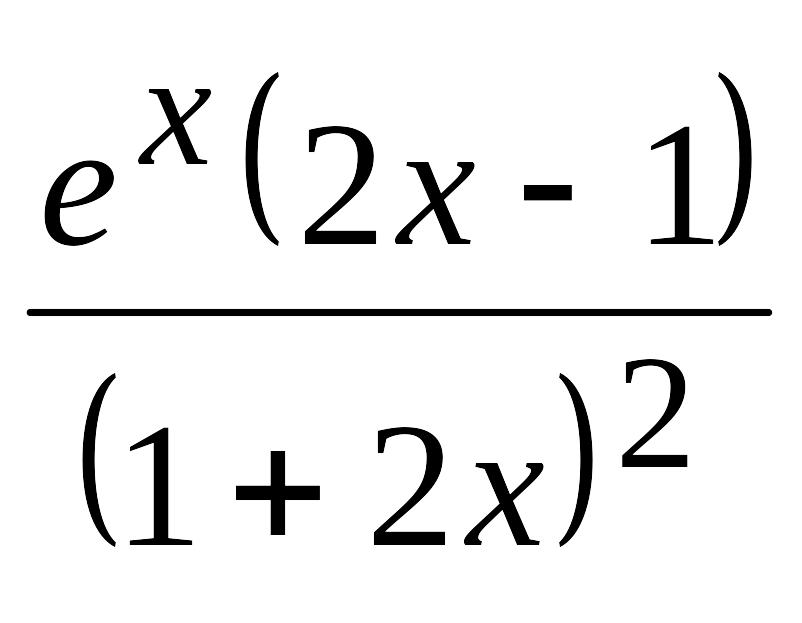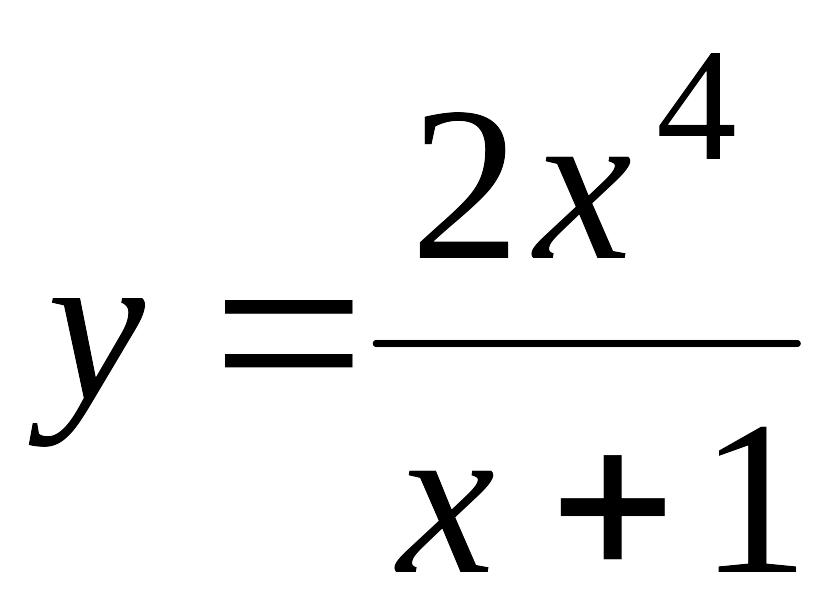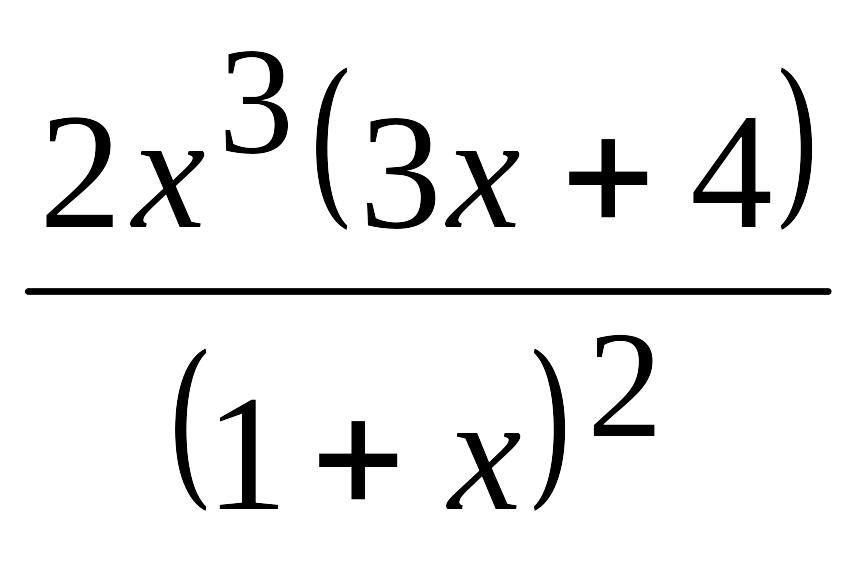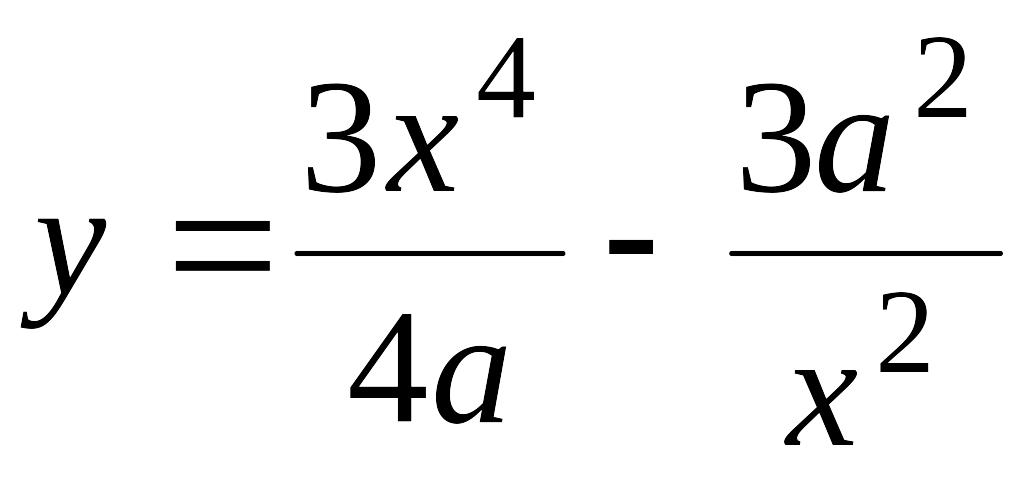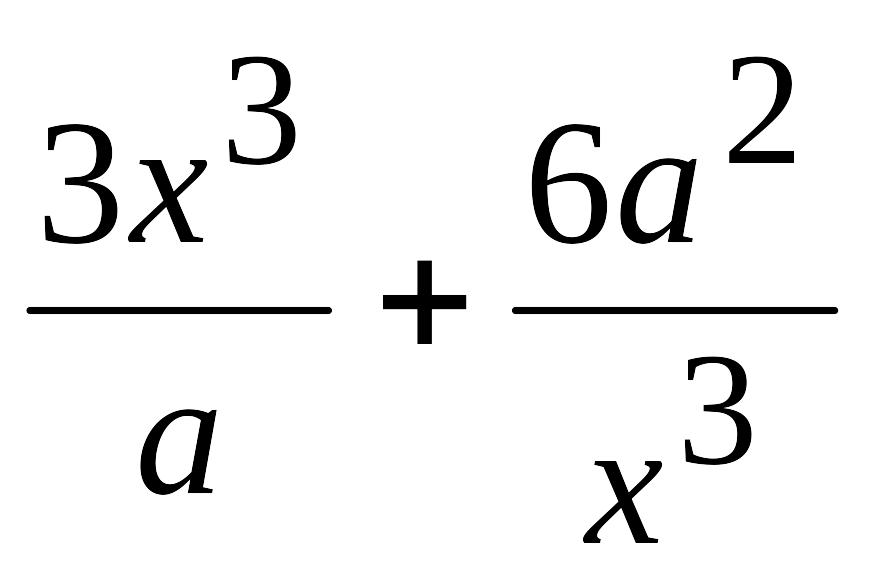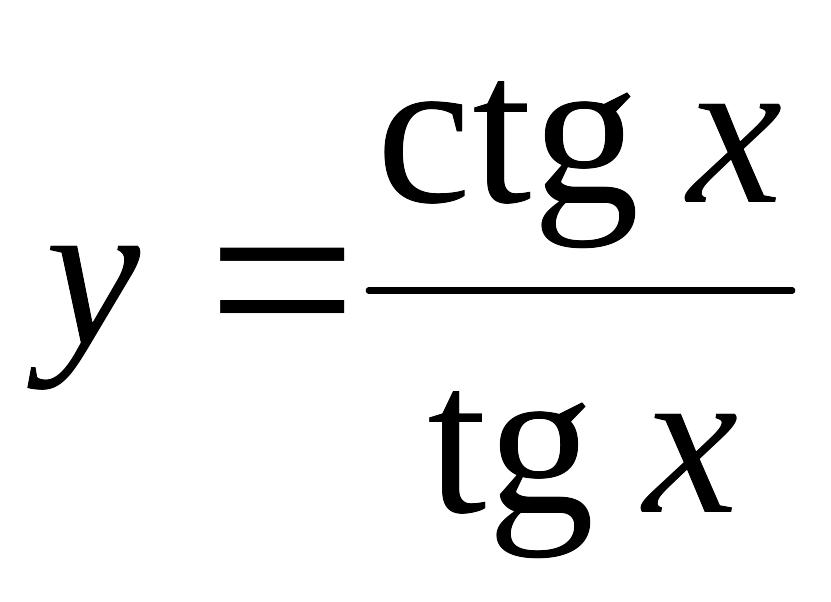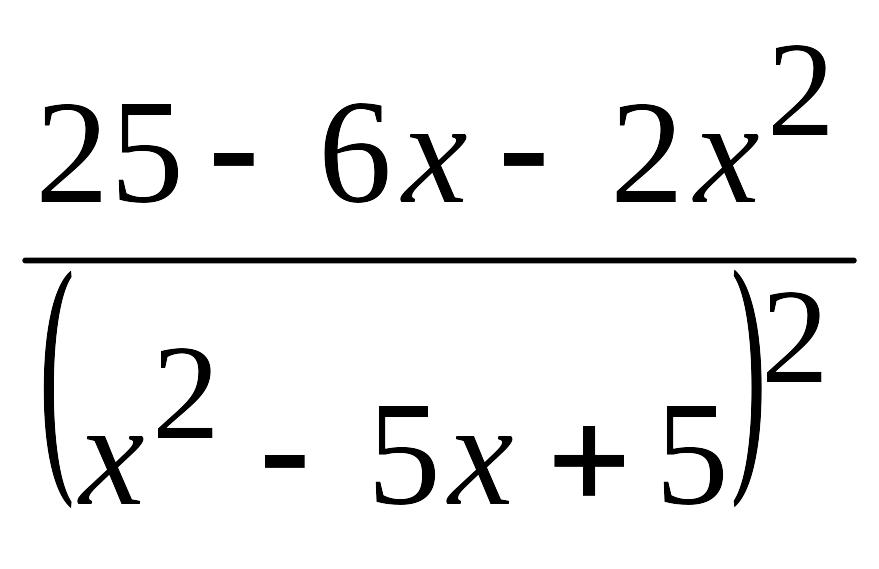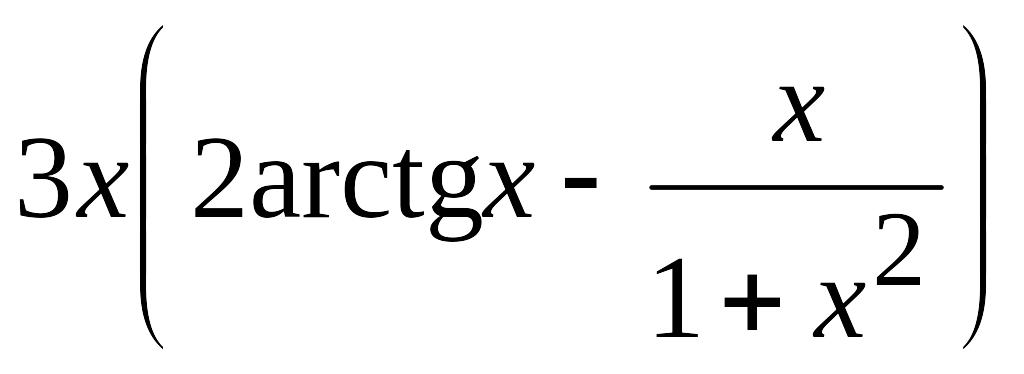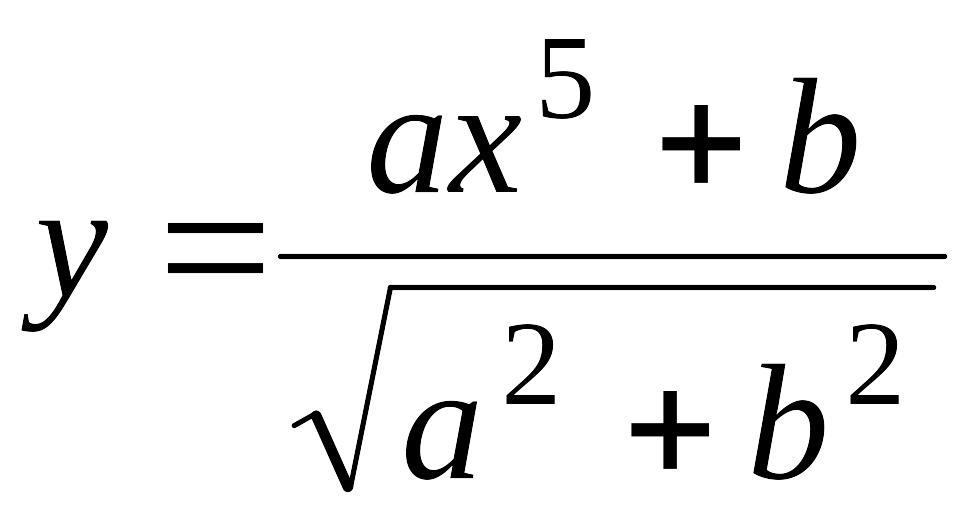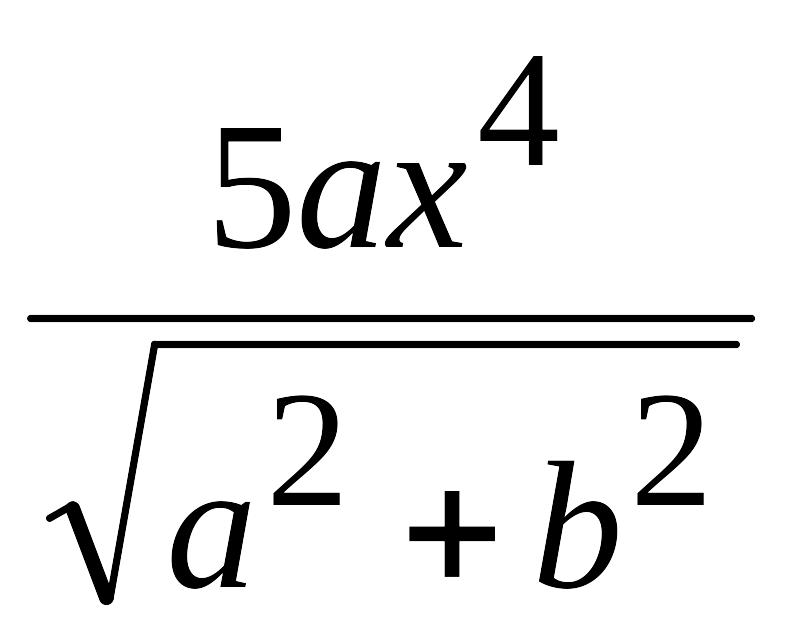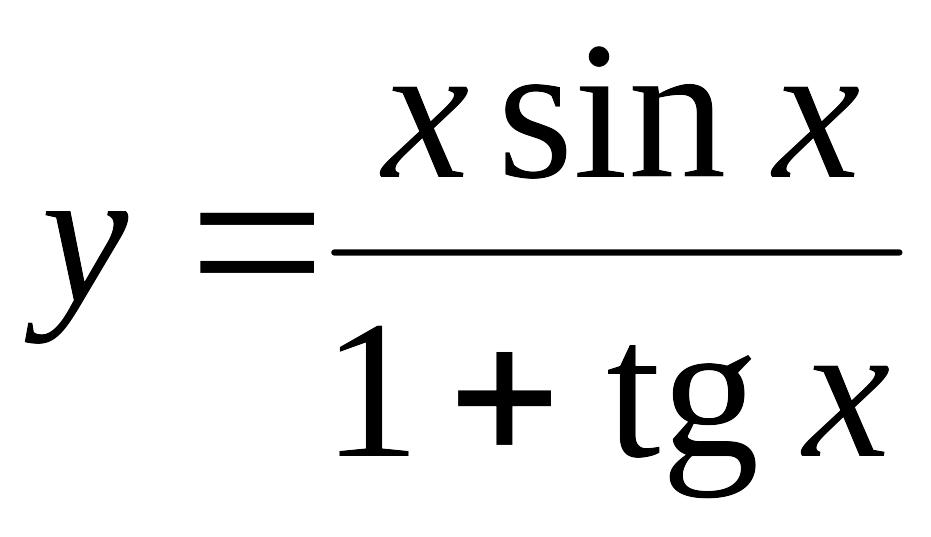
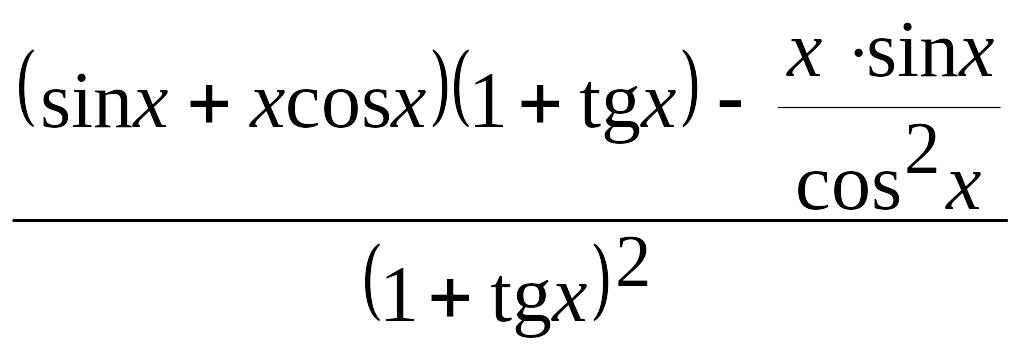Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности