
- •Содержание
- •«Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой»
- •Глава 1 пределы
- •Глава 2 дифференциальное исчисление функций одной независимой переменной
- •§ 1. Понятие производной
- •§2. Основные правила дифференцирования.
- •§3. Дифференцирование сложной функции.
- •§4. Производные высших порядков
- •§5. Дифференциал функции
- •Тогда, воспользовавшись формулой embed Equation.3 ,
- •§6. Применение производной при решении
- •Решение. Скорость прямолинейного движения
- •Глава 3 Исследование функций методами дифференциального исчисления
- •§1. Интервалы монотонности функции
- •Решение. Найдем производную заданной функции: embed Equation.3 .
- •§2. Экстремум функции
- •Глава 4 неопределенный интеграл4
- •§1. Непосредственное интегрирование.
- •Основные свойства неопределенного интеграла
- •§2.Интегрирование способом подстановки
- •§ 3. Интегрирование по частям.
- •Например:
- •§4. Применение неопределенного интеграла при решении прикладных задач.
- •Глава 5 определенный интеграл
- •§1.Определенный интеграл и его непосредственное
- •Основные свойства определенного интеграла
- •§2. Приложение определенного интеграла для вычисления площадей плоских фигур.
- •§3. Приложение определенного интеграла к решению физических задач.
- •Глава 6 дифференциальные уравнения
- •§1.Основные понятия.
- •§2.Уравнения с разделяющимися переменными.
- •§3. Однородные дифференциальные уравнения.
- •§4. Задачи на составление дифференциальных уравнений.
- •Глава 7 Элементы теории вероятностей и математической статистики
- •§ 1. Основные понятия
- •Вероятность случайного события – это количественная оценка объективной возможности появления данного события.
- •§ 2. Числовые характеристики распределения случайных величин
- •§4. Генеральная совокупность.
- •§5. Интервальная оценка. Интервальная оценка
- •§6. Проверка гипотез. Критерии значимости
- •§ 7. Элементы корреляционного и регрессионного анализа
- •7.1. Характер взаимосвязи между признаками
- •7.2. Проведение корреляционного анализа
- •7.3. Элементы регрессионного анализа
- •Статистическая обработка данных измерения роста.
- •Глава 4
- •Глава 5
- •Список литературы
- •614990, Г. Пермь,ул. Большевистская,85
«Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой»
Леонардо да Винчи,
G.36v (Записная книжка, 186 страница)
Глава 1 пределы
Постоянная
![]() является пределом функции
является пределом функции
![]() в точке
в точке
![]() ,
если их разность во всех точках, кроме
,
по абсолютному значению остается меньше
бесконечно малого положительного числа
.
,
если их разность во всех точках, кроме
,
по абсолютному значению остается меньше
бесконечно малого положительного числа
.
Если
для
![]() <,
то
<,
то
![]() .
.
Практическое вычисление пределов основывается на следующих теоремах:
Если
существуют![]() и
и
![]() то
то
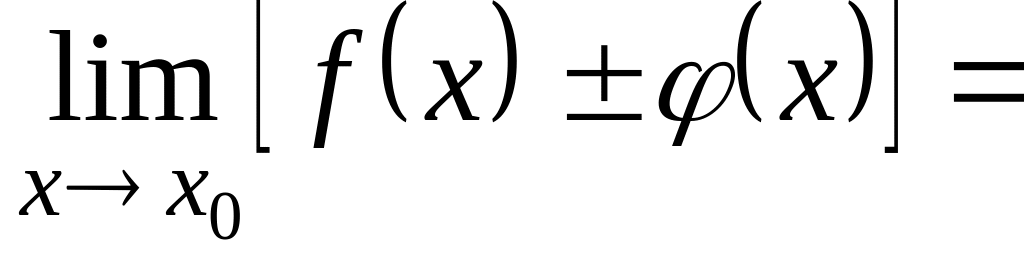

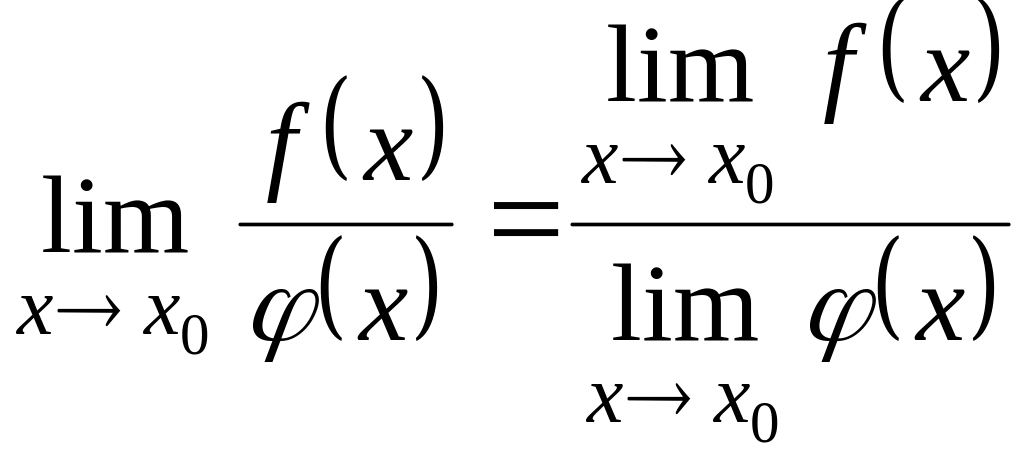 (при
≠0).
(при
≠0).
Используют также следующие пределы:
![]() -
первый замечательный предел
-
первый замечательный предел
![]() -
второй замечательный предел.
-
второй замечательный предел.
Иногда
в процессе отыскания предела при замене
аргумента определенным значением
функция получает выражение
![]() или
или
![]() - неопределенность. Хотя это выражение
не имеет определенного смысла, функция
может иметь конечный предел при данном
стремлении аргумента. Это становится
очевидным, если функцию преобразовать:
разложить ее на множители, или поделить
на аргумент, или умножить на сопряженное
выражение, и т.д.
- неопределенность. Хотя это выражение
не имеет определенного смысла, функция
может иметь конечный предел при данном
стремлении аргумента. Это становится
очевидным, если функцию преобразовать:
разложить ее на множители, или поделить
на аргумент, или умножить на сопряженное
выражение, и т.д.
Например:
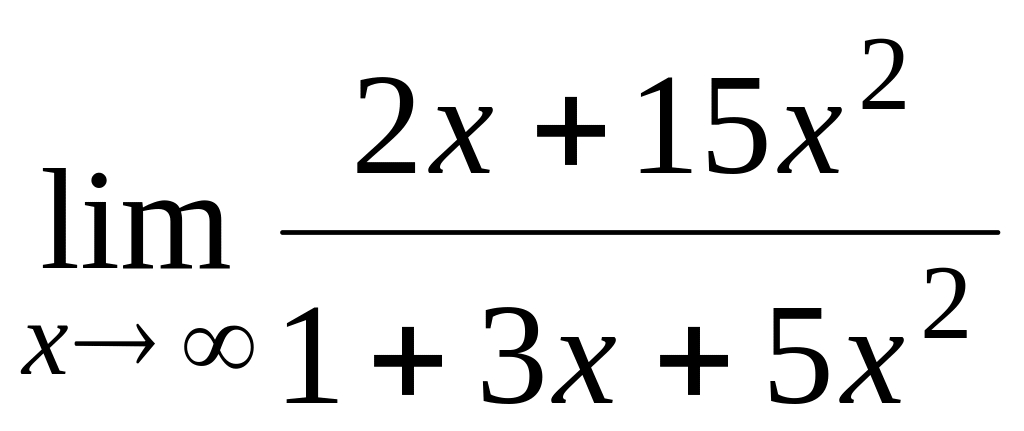 при
замене
при
замене
 преобразовывается в неопределенность
.
преобразовывается в неопределенность
.
Раскрыть
неопределенность можно, поделив все
члены выражения, стоящего под знаком
предела, на высшую степень аргумента,
то есть на
![]() :
:
=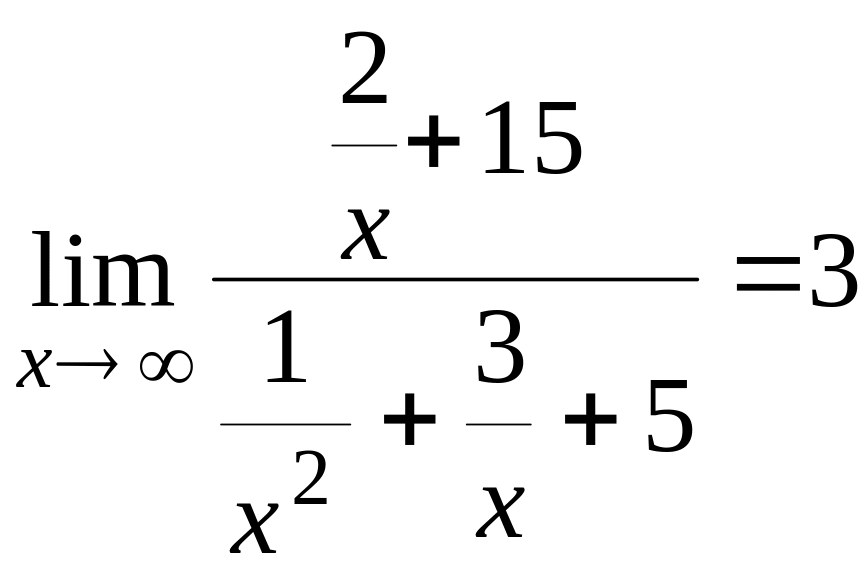 .
.
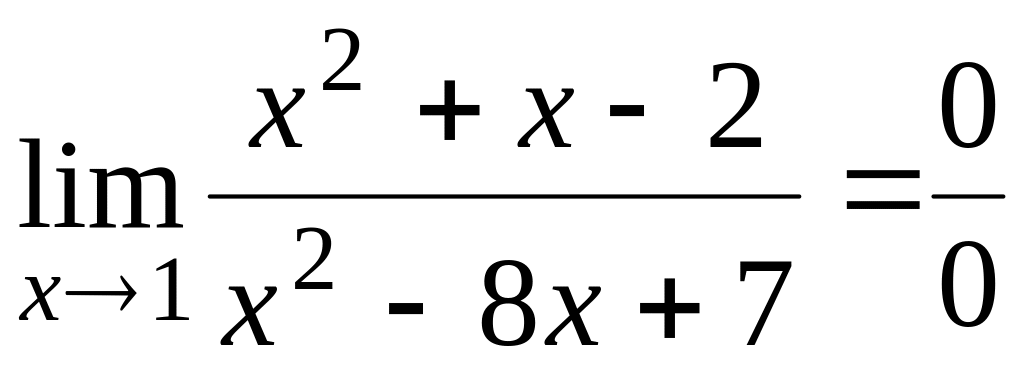 -
неопределенность.
-
неопределенность.
Раскрыть данную неопределенность можно, разложив выражения, стоящие в числителе и знаменателе под знаком предела, на множители, то есть:
![]()
![]()
![]()
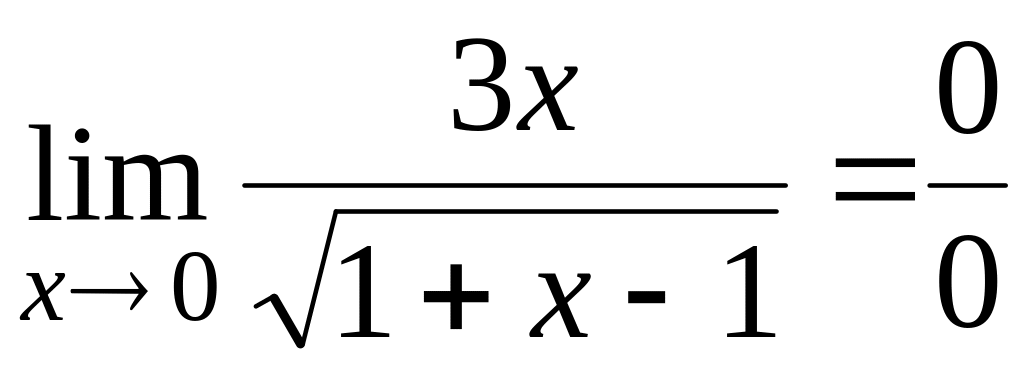 -
неопределенность.
-
неопределенность.
Умножив
и поделив выражение, стоящее под знаком
предела, на сопряженное выражение
![]() ,
получаем следующее выражение:
,
получаем следующее выражение:
![]()
![]()
=![]()
![]() .
.
Найти следующие пределы:
1.1.
(Ответ: 3) |
1.6.
|
1.2.
(Ответ: 1000) |
1.7.
|
1.3.
(Ответ:
|
1.8.
|
1.4.
|
1.9.
|
1.5.
|
1.10.
|
1.11.
|
1.21.
|
1.12.
|
1.22
|
1.13.
|
1.23.
|
1.14.
|
1.24.
|
1.15.
|
1.25.
|
1.16.
|
1.26.
|
1.17.
|
1.27.
|
1.18.
|
1.28.
|
1.19.
|
1.29.
|
1.20.
|
1.30.
|

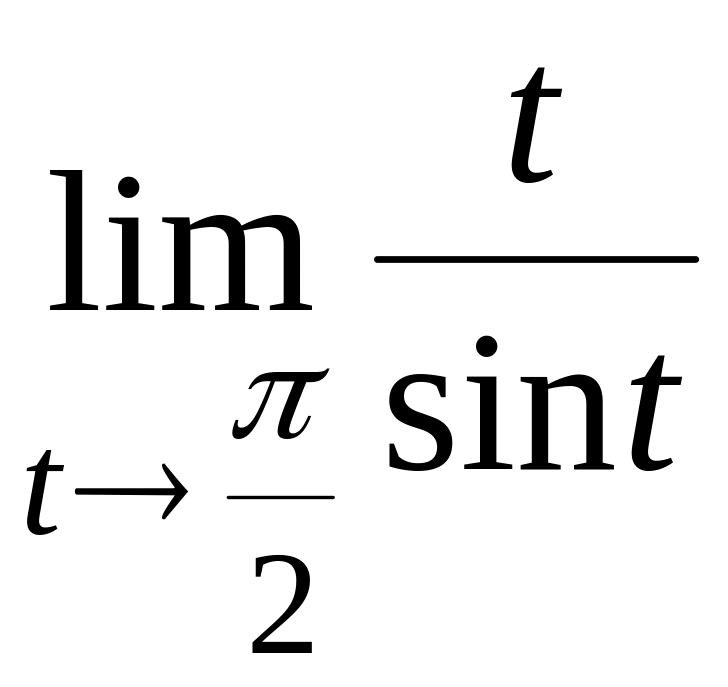 .
(Ответ:
.
(Ответ:
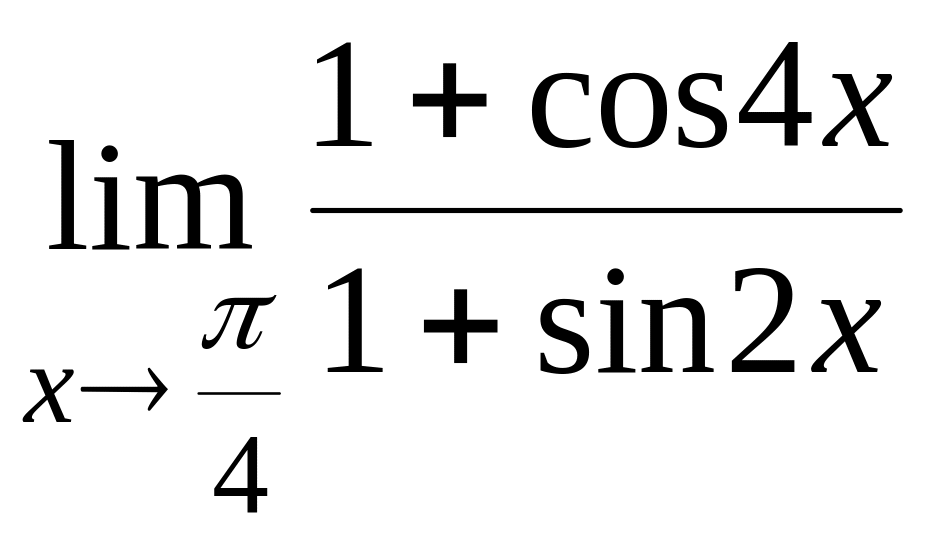 .
(Ответ: 0)
.
(Ответ: 0)