§ 2. Числовые характеристики распределения случайных величин

Обычно для описания распределения случайной величины бывает достаточно определить несколько числовых характеристик (параметров). Наиболее распространенные из них: математическое ожидание (среднее значение) случайной величины EMBED Equation.3 , дисперсия случайной величины EMBED Equation.3 и среднее квадратичное отклонение случайной величины EMBED Equation.3 .

Математическое ожидание – наиболее вероятное значение случайной величины. Для дискретных величин оно равняется сумме произведений каждого возможного значения EMBED Equation.3 на его вероятность EMBED Equation.3 : EMBED Equation.3

EMBED Equation.3 , (3)

где n-количество значений случайной величины.

Для непрерывных случайных величин математическое ожидание рассчитывается так: EMBED Equation.3

EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 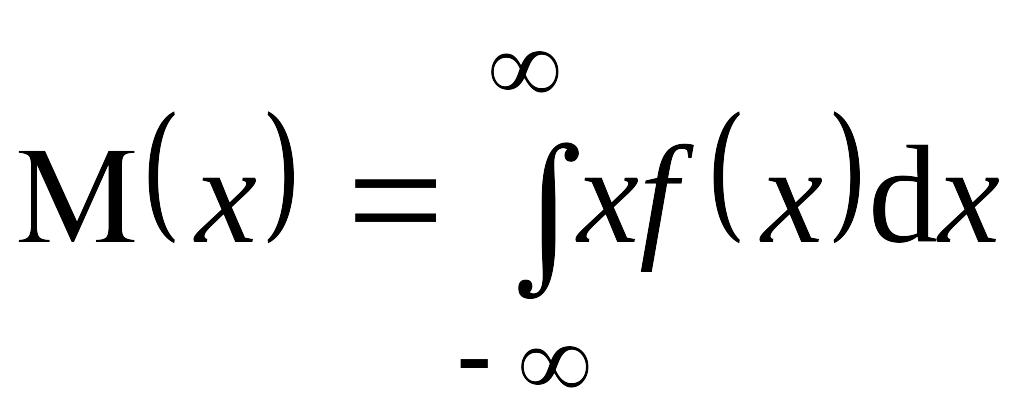. EMBED Equation.3 (4)

Дисперсия и среднее квадратичное отклонение является показателями рассеяния, вариации, изменчивости случайной величины.

Дисперсия - математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

EMBED Equation.3 . (5)

Для дискретных случайных величин дисперсия вычисляется как:

EMBED Equation.3 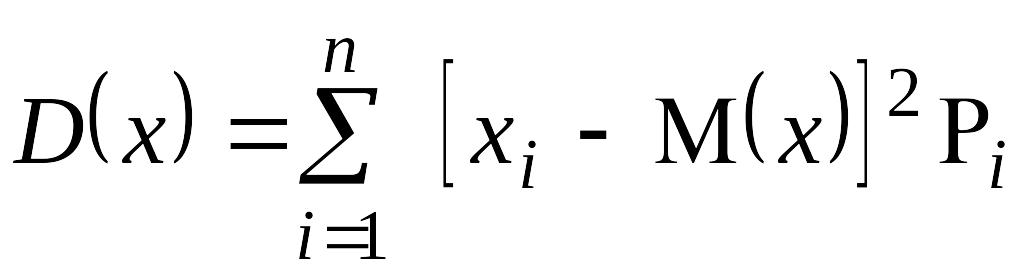, (6)

EMBED Equation.3 а для непрерывных случайных величин так:

EMBED Equation.3 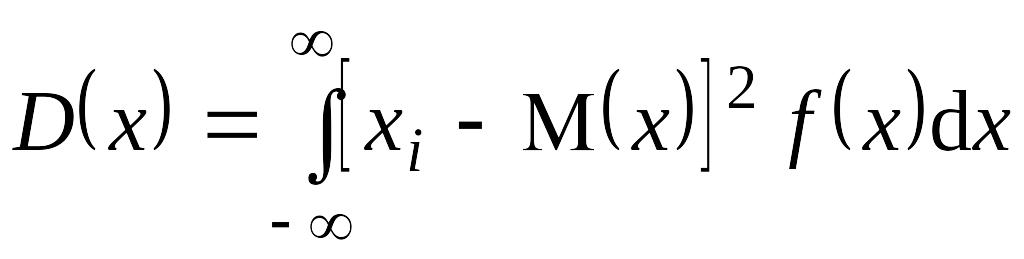. (7)

Среднее квадратичное отклонение вычисляется по формуле:

EMBED Equation.3 .

EMBED Equation.3 Эта величина равна среднему квадратичному отклонению случайной величины от ее математического ожидания. Она, в отличие от дисперсии, выражается в единицах той же размерности, что и изучаемая величина.

§3. Нормальный закон распределения случайных величин

Существуют различные законы распределения случайных величин. Для непрерывных величин наиболее распространенным является так называемый нормальный закон распределения или закон Гаусса. В соответствии с этим законом распределяются масса тела, рост человека, физиологические показатели и многое другое. В ряде случаев этот закон применим для анализа распределений дискретных случайных величин.

Функция плотности вероятностей нормального закона распределения случайных величин имеет следующий вид:

EMBED Equation.3 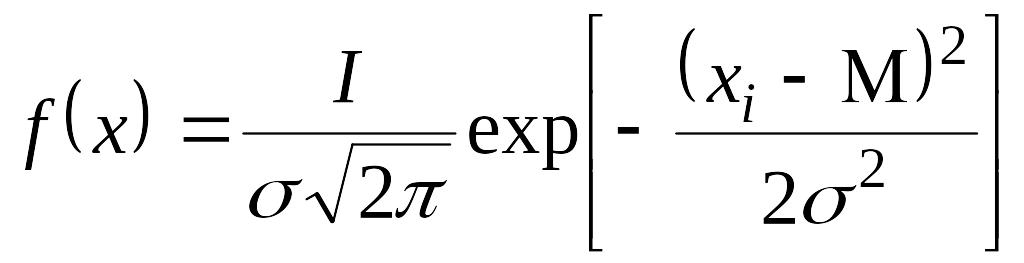, (9)

где EMBED Equation.3 – основание натурального логарифма, EMBED Equation.3 – математическое ожидание EMBED Equation.3 , EMBED Equation.3 среднее квадратичное отклонение случайной величины EMBED Equation.3 .

График этой зависимости называется кривой нормального закона распределения или кривой Гаусса (рис.1). Кривая имеет колоколообразную форму, она симметрична и асимптотически приближается к нулю. Из рисунка видно, что наиболее вероятным значением случайной величины является математическое ожидание EMBED Equation.3 . При отклонении величины EMBED Equation.3 в большую или меньшую сторону вероятность ее уменьшается.

EMBED PBrush 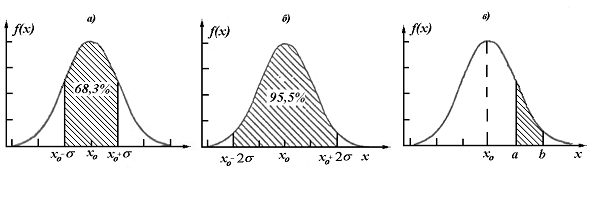Рис. 1

На кривой имеются две характерные точки, где выпуклость ее переходит в вогнутость. Абсциссы этих точек равны EMBED Equation.3 и EMBED Equation.3 .

Таблица 1

Интервал							Р,%
EMBED Equation.3	EMBED Equation.3		EMBED Equation.3		68,3
EMBED Equation.3		EMBED Equation.3		EMBED Equation.3		95,0
EMBED Equation.3		EMBED Equation.3		EMBED Equation.3		95,5
EMBED Equation.3		EMBED Equation.3		EMBED Equation.3		99,0
EMBED Equation.3		EMBED Equation.3		EMBED Equation.3		99,7
Здесь через EMBED Equation.3 обозначено EMBED Equation.3 .

Зная функцию плотностей вероятностей, можно рассчитать вероятность попадания случайной величины в заданный интервал значений EMBED Equation.3 . Например, вероятность попадания в интервал между значениями EMBED Equation.3 и EMBED Equation.3 равна:

EMBED Equation.3 ,

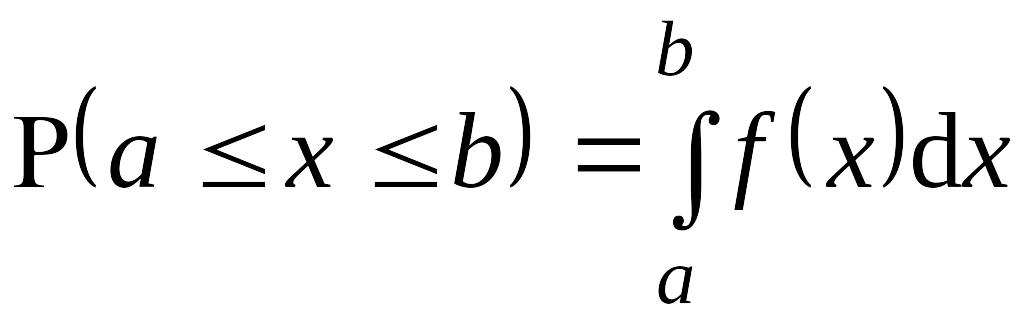или, графически, вероятность попадания оказывается равной площади криволинейной трапеции, заштрихованной на графике, приведенном на рис.1в.

Рассчитано (табл.1), что вероятность появления случайной величины в интервале EMBED Equation.3 составляет 0,68, в интервале EMBED Equation.3 – примерно 0,95, а в интервале EMBED Equation.3 вероятность появления случайной величины составляет 0,997.