Тема 6 Кінетика хіміко-технологічних процесів. Розрахунок кінетичних параметрів

6.1 Розрахункові формули швидкості процесів.

Будь-який хіміко-технологічний процес включає три основні стадії: 1) транспорт реагуючих речовин в зону реакції (наприклад, дифузійне перенесення реагенту з розчину до поверхні твердої фази через шар рідини, примикаючий до поверхні, і шар твердого продукту реакції); 2) хімічна реакція; 3) транспорт продуктів із зони реакції (наприклад, дифузійне перенесення розчиненого продукту реакції від поверхні реакції через шар твердого продукту реакції і рідини, що примикає до поверхні твердої фази, в об'єм розчину).

Загальна швидкість процесу залежить від швидкостей його окремих стадій і дорівнює швидкості найповільнішої (лімітуючої) стадії. Якщо лімітуючою є перша або третя стадія, то вважається, що процес протікає в дифузійній області. Якщо загальну швидкість процесу лімітують швидкості хімічних реакцій, то процес протікає в кінетичній області. Якщо ж швидкості всіх стадій близькі, то процес протікає в перехідній області.

Залежно від того, в якій області протікає процес, застосовуються різні вирази і прийоми для математичного опису і збільшення загальної швидкості процесу. Для процесів, що протікають в дифузійних областях, сумарну швидкість визначають з використанням рівняння для швидкості масопередачі, рівнянь дифузії і хімічної реакції. Типові прийоми розрахунків дифузійної кінетики розглянуті в розділі 5. в даному розділі розглянемо особливості протікання процесів в кінетичній області.

Швидкість процесу, що протікає в кінетичній області, тобто швидкість хімічної реакції W_Z(у кмоль/м3•с або кмоль/м2•с), виражається рівняннями:

для гомогенної реакції ; (6.1)

для гетерогенної реакції ; (6.2)

де V – об'єм реагуючих речовин, м³;

N – кількість речовини, що прореагувала або утворилася, кмоль;

F – поверхня контакту фаз, м²; τ – час, c.

Замість об'єму реагуючих речовин можна підставити об'єм реактора Vр, тоді

. (6.3)

При V = Vp = const,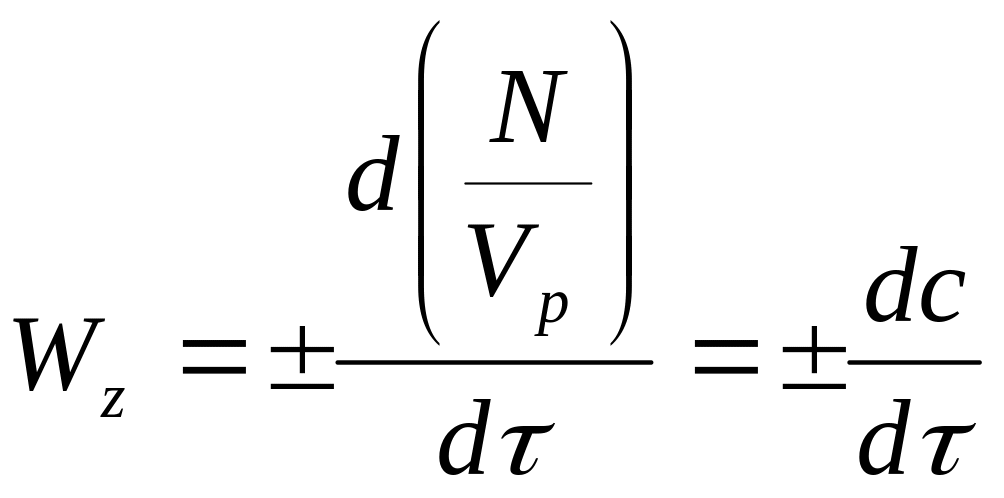 , (6.4)

де c – концентрація речовини, що є реагентом або продуктом в даній реакції, кмоль/м3.

Швидкість реакції пропорційна концентрацій реагуючих речовин в певній степені. Так, для модельної необоротної реакції аА+bB>dD, кінетичне рівняння матиме вигляд:

, (6.5)

де К – константа швидкості реакції (залежна від температури);

n_A, n_B – порядки реакції по відповідних реагуючих речовинах;

C_A, C_B – поточні концентрації речовин, що беруть участь в реакції.

Загальний порядок реакції (n=nA+nB) визначають експериментально і теоретично обґрунтовують, чому дана реакція має саме такий порядок (з'ясувавши механізм реакції). Найчастіше порядки реакції по реагуючих речовинах n_A і n_B не співпадають із стехіометричними коефіцієнтами реакції (а і b). Але, якщо стехіометричне рівняння правильно відображає механізм реакції (тобто має місце проста реакція, що протікає в одну елементарну стадію), то порядок реакції співпадає з її молекулярністю.

Швидкості перетворення різних компонентів, що беруть участь в реакції, пов'язані один з одним стехіометричними коефіцієнтами. Наприклад, якщо стехіометричне рівняння реакції має вигляд A+B>3D, то співвідношення між швидкостями перетворення компонентів запишеться:

. (6.6)

Тому необхідно вказувати, по якому компоненту визначена швидкість реакції (від цього залежатиме обчислюване значення константи швидкості реакцій).

Нехтуючи зміною об'єму в процесі реакції і беручи до уваги, що ступінь перетворення по речовині А в модельній реакції аА+bB>dD дорівнює, зміна концентрації речовини А в рівнянні (4.5) може бути виражена у вигляді:

при ,

де С_А0, Х_А – початкова концентрація і ступінь перетворення речовини А.

Тоді із законів стехиометрії зміна концентрації речовини В виражається рівнянням

,

де .

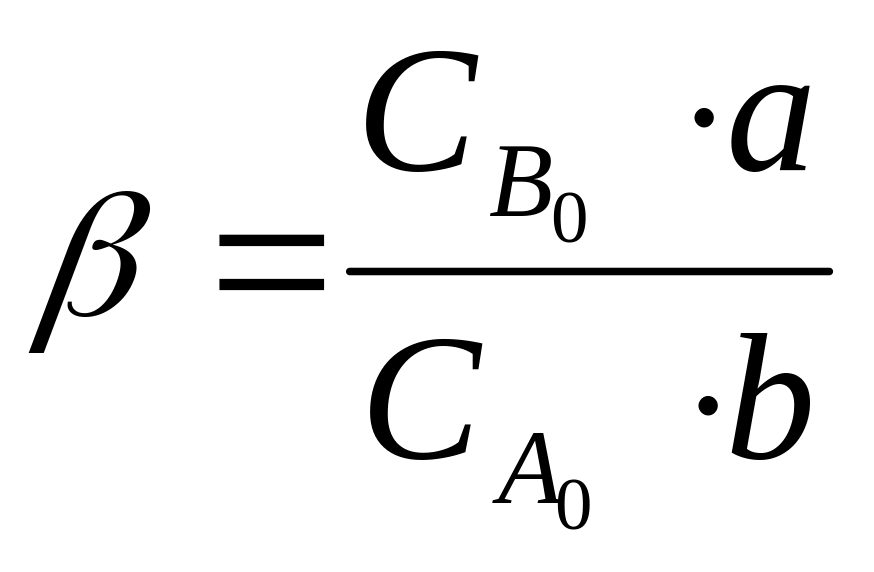Кінетичне рівняння (6.5) можна записати так:

.

Остаточно одержимо:

, (6.7)

де ; n – сумарний порядок реакції (n=nA+nB).

Якщо в системі протікає проста пряма і проста зворотна реакції aA+bB>dD і dD>aA+bB, то їх швидкості виражаються таким чином:

і .

В стані рівноваги хімічної системи швидкості прямої і зворотної реакції рівні.

. (6.8)

. (6.9)

Отже, рівняння (6.9) виявляє кінетичну роль К_С, яка визначає відношення констант швидкостей прямої і зворотної реакцій.

Проте в разі хімічної реакції, хоч і представляється одним стехіометричним рівнянням

, (6.10)

але протікаючої через декілька елементарних стадій, інтерпретація її кінетичного рівняння утруднена, а залежності між значеннями констант К₁ і К₂ при відомій величині К_С носять складніший характер.

Швидкість такої реакції можна визначити наступним рівнянням:

, (6.11)

що відображає залежність швидкостей як прямої, так і зворотної реакцій від концентрацій всіх компонентів, що беруть участь у взаємодії.

У рівнянні (6.11) показники степеня при концентраціях реагентів можуть бути цілими, дробовими, позитивними і негативними числами або дорівнювати нулю.

Для стану хімічної рівноваги, коли швидкість реакції по реагенту D рівна нулю (W_D=0), рівняння (6.11) матиме вид:

(6.12)

Константа хімічної рівноваги реакції (6.10) знаходиться таким чином:

(6.13)

Крім того, справедлива залежність

(6.14)

Рівняння (6.12) можна привести до виду:

(6.15)

Для ідеальних систем як Кс, так і К₁/К₂ залежать тільки від темпера-тури. Таким чином, з урахуванням виразів (6.14) і (6.15) справедлива залежність:

або (6.16)

Крім цього, повинні виконуватися умови:

; або

або , тобто (6.17)

показники степеня визначаються експериментально і не пов'язані із стехіометричними коефіцієнтами відповідних реагентів в рівнянні реакції. Проте вони повинні задовольняти умовам (6.17).

Приклад 6.1.

Для процесу отримання фосгену CO+Cl₂-COCl₂, експериментально встановлено, що швидкість утворення продукту описується кінетичним рівнянням

Визначити М.

Розв`язок.

Згідно стехіометричному рівнянню, константу хімічної рівноваги цієї реакції можна представити рівнянням

або, що рівноційно, співвідношенням .

Показники степеня у встановленому експериментально кінетичному рівнянні мають наступні значення:

тобто М=1. Відношення К₁/К₂ зводиться до виду вираження К_С, наступ-ному із стехіометричного рівняння реакції.

Приклад 6.2.

При утворенні азотної кислоти стехіометричні відношення можуть бути представлені рівнянням 3N₂O₄ + H₂O = 4HNO₃ + 2NO

Швидкість цієї реакції при постійній концентрації азотної кислоти має вид:

В цьому випадку

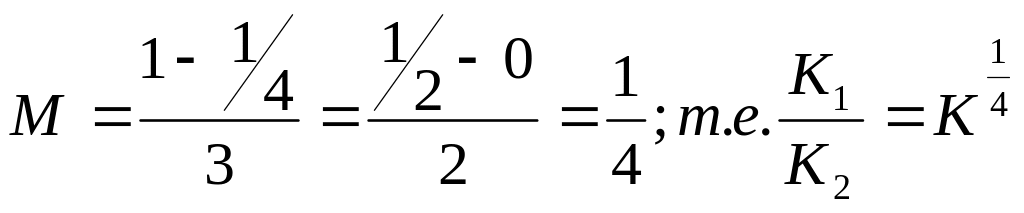
Загальне трактування кінетики послідовних реакцій пов'язане з складними залежностями. У простому випадку реакція відбувається відповідно до рівняння

(6.18)

Якщо обидві проміжні реакції необоротні, мають n=1, а реакційна система має постійний об'єм, то

(6.19)

; (6.20)

(6.21)

З рівняння (6.18) виходить, що якщо

(6.22)

Інтегруючи рівняння (6.19) в межах 0, τ і С_А0,С_А, одержуємо:

або (6.23)

Підставивши (6.23) в (6.20), одержимо лінійне диференціальне рівняння першого порядку:

(6.24)

Розв’язок цього рівняння дає хід зміни концентрації реагенту В в часі:

(6.25)

Враховуючи (6.22)….(6.24), знаходимо вираз, що описує зміну концентрації продукту D під час протікання реакції

, (6.26)

яке спрощується при К₂>>К₁ і К₁>>К₂.

Диференціюючи рівняння (6.25) і прирівнюючи нулю , можна визначити момент, в який концентрація напівпродукту В досягне максимальної величини:

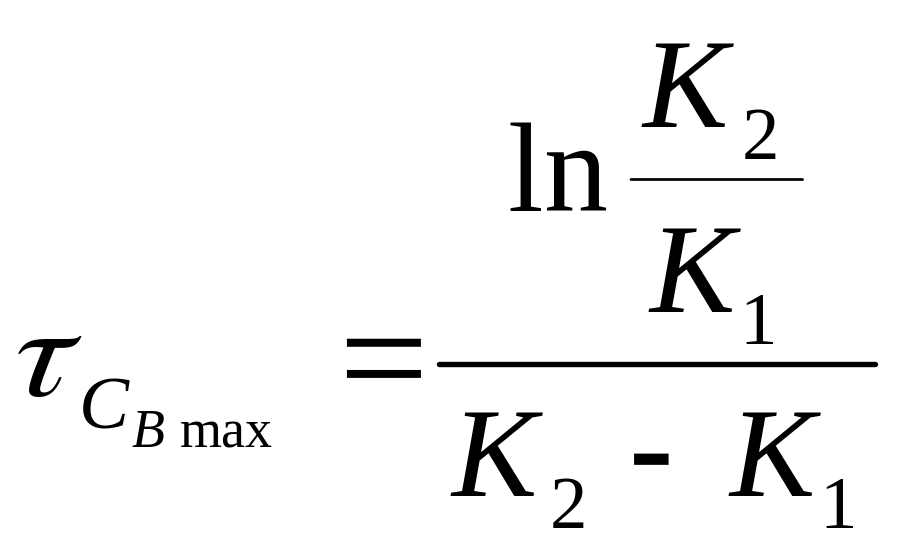(6.27)

З рівнянь (6.25) і (6.27) знаходиться чисельне значення максимальної концентрації В :

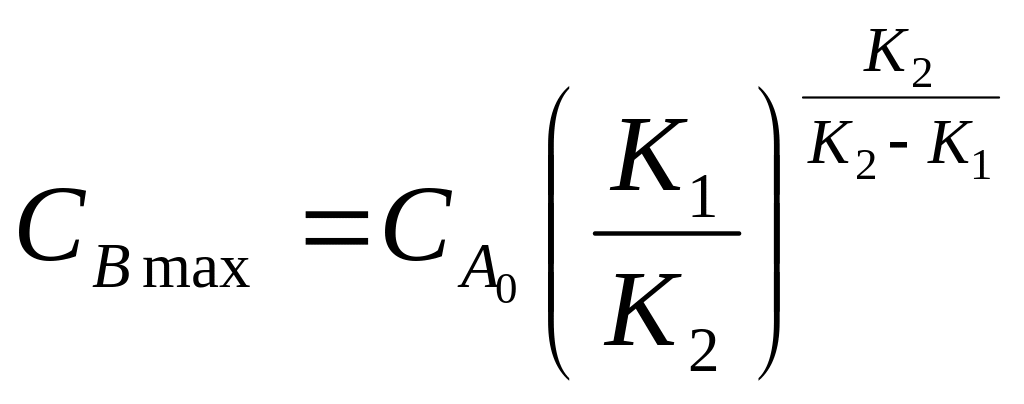(6.28)

Дуже часто в хімічних процесах одночасно з основним перетворенням має місце одна або декілька побічних реакцій. Найпростіший приклад – дві паралельні необоротні реакції першого порядку, протікаючі при постійному об'ємі:

Звідси, проінтегрувавши останній вираз, одержуємо:

Розділивши на , маємо: і після інтеграції: (при ).

У складних реакціях такого типу не можна встановити константи швидкостей по зміні концентрації тільки одного реагенту в часі. Визначивши концентрації двох реагентів, концентрацію третього знаходимо по балансовому рівнянню С_А+С_В+С_D=const. Потім розраховуємо значення констант швидкостей, використовуючи кінетичні рівняння для, , .