1. Метод корреляции

Рис. .1 иллюстрирует идею метода корреляции. Здесь показаны два снимка (левый и правый) составляющих стереопару. Предположим, что выбрали точку (черный пиксель) соответственная точка на правом снимке также черный пиксель. Координаты точки на левом снимке известны, а координаты соответственной точки на правом снимке хотим получить. Для этого выделяется фрагмент изображения на левом снимке (его часто называют эталонной матрицей) с центром в определяемой точке и как бы накладывается на правый снимок (матрица поиска), как показано на рис. .2, и перемещается по направлениям x и y с шагом один пиксель. Для каждого положения эталонной матрицы вычисляется коэффициент корреляции R. Положение матрицы, при котором значение коэффициента корреляции является максимальным, соответствует идентичной (искомой на правом снимке) точке. Таким образом, находят координаты соответственной точки на правом снимке. Коэффициент корреляции R изменяется в пределах от 0 до 1.

Коэффициент корреляции вычисляется по следующей формуле:

( .1)

Где f₁, f₂ – плотности пикселей эталонной матрицы и матрицы поиска соответственно, т.е. левого и правого изображений; i – номер пикселя в матрице; n – количество пикселей в матрице (например, на рис. .1 матрица имеет размерность 5х7, поэтому n=35); x₁,y₁ и x₂,y₂ - координаты центрального пикселя матрицы на левом и правом снимке соответственно. Иногда вместо исходных плотностей f₁, f₂ используют их значения после фильтрации, или значения градиентов, и т.д. Если пара снимков отличается друг от друга по тону изображения, то в этом случае целесообразно вычислить среднее значение плотностей пикселей для каждого изображения и затем вычесть это среднее из каждого пикселя, как для левого, так и для правого снимков. Т.е. вычисляют нормализованное значение коэффициента корреляции:

где

Рис. .2

Теперь попробуем объяснить формулу ( .1) с геометрической точки зрения. Для этого представим все элементы эталонной матрицы и матрицы поиска как координаты векторов в n мерном пространстве (n – число элементов в эталонной матрице) и обозначим эти векторы через f₁, f₂. Из аналитической геометрии известно, что два вектора совпадают (равны) когда равны значения координат этих векторов и как следствие угол между этими векторами равен нулю. Значение угла между двумя векторами вычисляется по известной формуле:

( .2)

когда два вектора коллинеарны (совпадают), так как . Если сравнить формулы ( .1) и ( .2) видим, что они одинаковые. Другими словами, коэффициент корреляции R представляет собой косинус угла между векторами в n пространстве, координаты которых значения плотностей пикселей. Таким образом, R=1 в том случае, когда все значения плотностей пикселей (координаты векторов) двух изображений равны между собой ( ).

Для положения эталонной матрицы, когда R принимает максимальное значение, получаем соответственную точку на правом снимке с координатами x₂,y₂. Таким образом, можно получать координаты соответственных точек на правом снимке с точностью шага перемещения эталонной матрицы по матрице поиска (в данном случае – один пиксель). Для получения координат с подпиксельной точностью можно уменьшить шаг перемещения эталонной матрицы, например, установить его равным 0.1 пикселя. В этом случае необходимо увеличить изображения в 10 раз, т.е. один пиксель исходного изображения занимает 10х10 пикселей в увеличенном изображении. На

Рис. .3

рис. .3 показан пример получения увеличенного изображения в два раза. Если осуществлять корреляцию по таким изображениям, то точность определения координат будет равна 0.5 пикселя.

Существует другой метод получения подпиксельной точности. Сначала выполняют корреляцию с точностью один пиксель, затем выбирают дискретные значения коэффициентов корреляции R вокруг пикселя с R_max и описывают их непрерывной функцией. Найдя локальный экстремум этой функции можно найти координаты x,y с подпиксельной точностью. В качестве примера этой функции рассмотрим полином второй степени, который описывает поверхность образованную коэффициентами корреляции, причем раздельно по каждой координатной оси (рис. .4):

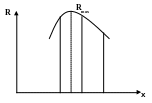
Рис. .4

( .3)

Для нахождения локального экстремума этой функции воспользуемся известным положением, что производные функции по x,y в точке экстремума R_max равны нулю, тогда соответствующие координаты можно найти по следующим формулам:

( .4)

Для описания поверхности, образованной коэффициентами корреляции можно применить и другой полином, например, следующий:

( .5)