Kurant_R__Robbins_G_-_Chto_takoe_matematika_-_2015

§ 3 ДВОЙНОЕ ОТНОШЕНИЕ 201

До сих пор, говоря о двойном отношении четырех точек A, B, C, D, расположенных на прямой l, мы предполагали, что это отношение составлено из положительных отрезков. Целесообразно видоизменить это определение следующим образом. Примем одно из двух направлений прямой l за положительное и условимся, что все отрезки, отсчитываемые в этом

парой точек C, D или не разделена. Так как свойство «разделяться» инвариантно относительно проектирования, то понимаемое в новом смысле (как

зок AB внутренне и внешне в одном и том же отношении. В этом случае принято говорить, что C и D делят отрезок AB гармонически, и каждая из точек C и D считается гармонически сопряженной с другой точкой относительно пары точек A, B. Если (ABCD) = 1, то точки C и D (или A и B) совпадают.

202 ПРОЕКТИВНАЯ ГЕОМЕТРИЯ. АКСИОМАТИКА гл. IV

Необходимо не упустить из виду, что при определении двойного отношения (ABCD) существенную роль играет порядок, в котором берутся точки A, B, C, D. Например, если (ABCD) = l, то двойное отноше-

ние (BACD) равно l1 , тогда как (DACB) = 1 − l, в чем читатель убедит-

ся без труда. Четыре точки A, B, C, D могут быть переставлены между собой 4 · 3 · 2 · 1 = 24 различными способами, и каждой перестановке соответствует некоторое значение двойного отношения. Некоторым перестановкам соответствует то же числовое значение двойного отношения, что и начальной перестановке A, B, C, D; например, (ABCD) = (BADC). Читателю предоставляется в качестве упражнения доказать, что при 24 возможных перестановках четырех точек получается всего лишь шесть

Эти шесть величин, вообще говоря, различны, но при некоторых значениях l могут и совпадать по две, например при значении l = −1 в случае гармонического деления.

Мы можем также определить двойные отношения четырех компланарных (т. е. лежащих в одной плоскости) и конкуррентных прямых 1, 2, 3, 4, как двойное отношение четырех точек пересечения этих прямых с некоторой прямой, лежащей в той же плоскости. Положение этой пятой прямой несущественно вследствие инвариантности двойного отношения при проектировании. Эквивалентным этому определению является следу-

ющее:

(1234) = ±sin(1,sin(2, 3)3) : sin(1,sin(2, 4)4) ,

где нужно взять знак плюс, если пара прямых 1, 2 не разделяется парой 3, 4, и знак минус, если разделяется. (В этой формуле (1, 3), например, обозначает угол между прямыми 1 и 3.) Наконец, можно определить двойное отношение четырех коаксиальных плоскостей (четырех плоскостей, пересекающихся по одной прямой, или «оси»). Если некоторая прямая пересекает плоскости в четырех точках, то двойное отношение этих точек

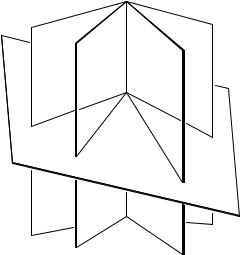
всегда будет иметь одно и то же значение, независимо от выбора прямой (доказательство предлагается в качестве упражнения). Таким образом, полученное значение можно назвать двойным отношением рассматриваемых четырех плоскостей. Иначе, можно назвать двойным отношением четырех коаксиальных плоскостей двойное отношение четырех прямых, по которым они пересекаются произвольной пятой плоскостью (рис. 79).

Рис. 79. Двойное отношение четырех плоскостей

Понятие двойного отношения четырех плоскостей побуждает поставить вопрос о том, нельзя ли дать определение проективного преобразования трехмерного пространства самого на себя. Определение с помощью центральной проекции, очевидно, не обобщается непосредственно от случая двух измерений на случай трех измерений. Но можно доказать, что каждое непрерывное преобразование плоскости самой на себя, взаимно однозначно переводящее точки в точки и прямые в прямые, есть проективное. Это обстоятельство наводит на мысль ввести следующее определение для случая трех измерений: проективным преобразованием пространства называется непрерывное взаимно однозначное преобразование, переводящее прямые линии в прямые линии. Можно показать, что такие преобразования оставляют значения двойных отношений неизменными.

Добавим к предыдущему еще кое-какие замечания. Пусть на прямой даны три различные точки A, B, C с координатами x1, x2, x3. Требуется найти четвертую точку D таким образом, чтобы удовлетворялось равенство (ABCD) = l, где l задано. (Частный случай, когда l = −1 и задача

204 ПРОЕКТИВНАЯ ГЕОМЕТРИЯ. АКСИОМАТИКА гл. IV

заключается в построении четвертой гармонической точки, будет подробно рассмотрен в следующем пункте.) Вообще говоря, задача имеет одно и только одно решение; действительно, если x — координата искомой точ-

имеет ровно одно решение. Считая x1, x2 и x3 заданными и полагая ради

краткости x3 − x1 = k, мы придадим решению вид x3 − x2

x = kx2 − x1 . k − l

Например, если точки A, B, C находятся на равных расстояниях друг от друга и имеют соответственно координаты x1 = 0, x2 = d, x3 = 2d, то тогда k = 22dd −− d0 = 2 и x = 22−dl .

O′′

O′

A′′

B′′

D′′

l′′

Рис. 80. Проективное соответствие между точками двух прямых

Если прямая l спроектирована из двух различных центров O′ и O′′ на две различные прямые l′ и l′′, то получается соответствие P ←→ P′ между точками прямых l и l′ и соответствие P ←→ P′′ между точками прямых l и l′′. Этим устанавливается соответствие P′ ←→ P′′ между точками прямых l′ и l′′, и притом такое, что каждые четыре точки A′, B′, C′, D′ на l′ имеют то же самое двойное отношение, что и соответствующие точки A′′, B′′,

C′′, D′′ на l′′. Всякое взаимно однозначное соответствие между точками двух прямых, обладающее этим свойством, называется проективным соответствием, независимо от того, каким способом это соответствие установлено.

Упражнения. 1) Докажите, что если даны две прямые вместе с проективным соответствием, установленным между ними, то можно подвергнуть одну из прямых такому параллельному перенесению, что заданное соответствие будет получаться посредством простой проекции. (Указание: совместите какую-нибудь пару взаимно соответствующих точек на данных прямых.)

2) Пользуясь предыдущим результатом, покажите, что если между точками двух прямых l и l′ установлено соответствие посредством конечного числа последовательных проектирований на различные промежуточные прямые при произвольных центрах проекций, то тот же результат может быть получен посредством всего лишь двух проектирований.

E

I

H

F

G

A C B D

Рис. 81. Полный четырехсторонник

2. Применение к полному четырехстороннику. В качестве интересного применения инвариантности двойного отношения мы докажем одну простую, но важную теорему проективной геометрии. Речь идет о полном четырехстороннике — фигуре, образованной произвольными четырьмя прямыми, из которых никакие три не являются конкуррентными, и шестью точками их пересечения. На рис. 81 названные четыре прямые суть AE, BE, BI, AF. Прямые AB, EG и IF являются диагоналями четырехсторонника. Рассмотрим одну из диагоналей, например AB, и отметим на ней точки C и D, где она пересекается с двумя другими диагоналями. Тогда теорема утверждает существование равенства (ABCD) = −1; словами это

выражается так: точки пересечения одной диагонали с двумя другими делят отрезок между вершинами четырехсторонника гармонически. Для доказательства достаточно обратить внимание на то, что

Как нам известно,

(BACD) = 1 ;

(ABCD)

таким образом, x = x1 , x2 = 1, x = ±1. Но так как C, D разделяют A, B,

то двойное отношение x отрицательно и потому оно должно быть равно именно −1, что мы и хотели доказать.

Полученное замечательное свойство полного четырехсторонника дает нам возможность с помощью одной лишь линейки построить точку, гармонически сопряженную с точкой C относительно пары A, B (если A, B, C коллинеарны). Нужно только, выбрав произвольную точку E вне данной прямой, провести прямые EA, EB, EC; затем, взяв произвольно точку G на EC, провести прямые AD и BD, пересекающие EB и EA, скажем, в точках F и I; провести, наконец, прямую IF, которая и пересечет исходную прямую в искомой точке D.

Рис. 82. Проведение прямой через препятствие

Задача. На плоскости задан отрезок AB и область R, как показано на рис. 82. Желательно продолжить прямую AB вправо от R. Как это можно сделать с помощью одной линейки и при условии, чтобы в процессе построения не покрывать линейкой никакой части области R? (Указание: выберите на отрезке AB две произвольные точки C и C′, затем постройте сопряженные с ними гармонические D и D′ относительно пары точек A, B; при построении воспользуйтесь четыре раза теоремой о полном четырехстороннике.)

§4. Параллельность и бесконечность

1.«Идеальные» бесконечно удаленные точки. Внимательное рассмотрение изложенного в предыдущем параграфе обнаруживает, что во многих случаях приведенная аргументация теряет силу — именно, тогда, когда прямые, точка пересечения которых нужна для построения, оказываются параллельными. Например, построение четвертой гармонической

точки D становится невыполнимым, если прямая IF параллельна AB. Геометрические рассуждения на каждом шагу затруднены тем обстоятельством, что параллельные прямые не имеют общей точки, и потому всякий раз, когда речь идет о пересечении прямых, приходится отдельно рассматривать и особо оговаривать случай параллелизма. С другой стороны, если производится проектирование, мы вынуждены различать и трактовать независимо рядом с центральной также и параллельную проекцию. Если бы из такого положения не было выхода, то проективная геометрия, будучи вынуждена вникать в детальное исследование каждого встречающегося исключения и особого случая, неизбежно была бы чрезвычайно усложнена. Все это побуждает искать выхода в ином направлении, именно, на пути такого обобщения основных понятий, которое устраняло бы возможные исключения.

Тут нам поможет геометрическая интерпретация; мы видим, что если прямая, пересекающая другую прямую, медленно вращается, приближаясь к положению параллельности, то точка пересечения двух прямых неограниченно удаляется. Это дает повод к наивному утверждению: две прямые пересекаются «в бесконечно удаленной точке». Подобного рода формулировке существенно придать точный смысл с таким расчетом, чтобы с «бесконечно удаленными», или, как иногда говорят, с «идеальными» точками можно было проводить точные и надежные рассуждения, как с обыкновенными точками на плоскости или в пространстве. Иными словами, мы желали бы, чтобы все правила поведения точек, прямых, плоскостей оставались в силе и для «идеальных» геометрических элементов.

В математическом смысле существование «бесконечно удаленных точек» обеспечено, если отчетливо и без взаимных противоречий установлены математические свойства этих вновь вводимых элементов, т. е. их взаимоотношения с «обыкновенными» точками и между собой. Обыкновенно система геометрических аксиом (например, в евклидовой геометрии) вытекает путем абстракции из наблюдений над физическими объектами: таковы следы прикосновения карандаша к бумаге или мела к доске, натянутые нити, световые лучи, твердые стержни и т. п. Свойства, приписываемые аксиомами математическим точкам и прямым, представляют собой в высшей степени упрощенные и идеализированные описания поведения соответствующих им физических «двойников». Через любые два карандашных пятнышка можно провести не одну, а много карандашных «прямых». Если пятнышки становятся все меньше по диаметру, то все такие «прямые» станут трудно отличимыми одна от другой. Вот что мы, собственно говоря, имеем в виду, высказывая в качестве геометрической аксиомы, что «через любые две точки можно провести одну и только одну прямую»: мы при этом говорим об «абстрактных», чисто умозрительных, геометрических точках и прямых. Геометрические точки и прямые обладают гораздо более простыми

свойствами, чем какие бы то ни было физические объекты. Упрощение является существенным условием, позволяющим строить геометрию как дедуктивную дисциплину.

Как уже было отмечено, обыкновенная геометрия точек и прямых весьма осложнена тем обстоятельством, что две параллельные прямые не имеют точки пересечения. Это побуждает нас сделать дальнейшее упрощение в структуре геометрии, расширяя понятие геометрической точки таким образом, чтобы устранить указанное исключение — совершенно так же, как мы расширяли понятие числа с целью устранения ограничений при вычитании и делении. В геометрии, как и в арифметике, мы озабочены неукоснительно сохранением в расширенной области тех законов, какие регулировали отношения в первоначальной области.

Итак, мы уславливаемся в том, что к обыкновенным точкам всякой прямой добавляем еще одну, «идеальную», точку и будем считать эту точку принадлежащей одновременно всем прямым, параллельным данной, и никаким другим. Следствием такого условия является то, что всякая пара прямых на плоскости теперь уже пересекается в единственной точке: если прямые не параллельны, то в «обыкновенной» точке; если параллельны, то в им обеим принадлежащей «идеальной» точке. По причинам интуитивного порядка эта идеальная точка на прямой называется бесконечно удаленной точкой на этой прямой.

Интуитивное представление о точке, удаляющейся в бесконечность по прямой линии, могло бы навести на мысль, что следует добавить две идеальные точки на каждой прямой — по одной для каждого направления. Если мы добавляем только одну, то лишь потому, что мы заинтересованы в сохранении закона: через каждые две точки проходит одна и только одна прямая. Если бы прямая содержала две бесконечно удаленные точки вместе со всеми, ей параллельными, то вышло бы, что через две такие «точки» проходит бесконечное множество прямых.

Мы уславливаемся также в том, что к обыкновенным прямым на плоскости добавляем еще одну «идеальную», так называемую

«бесконечно удаленную» прямую, содержащую все бесконечно удаленные точки плоскости и никаких других. Мы вынуждены принять именно такое условие, если хотим сохранить первоначальный закон — «через всякие две точки проходит одна прямая» и вновь утвержденный закон — «всякие две прямые пересекаются в одной точке». В самом деле, возьмем две какие-нибудь идеальные точки. Единственная прямая, которая должна проходить через эти точки, не может быть обыкновенной прямой, так как по принятому условию каждая обыкновенная прямая содержит только одну идеальную точку. С другой стороны, эта прямая не может содержать обыкновенных точек, так как через обыкновенную точку и одну из идеальных точек непременно прошла бы обыкновенная прямая. Наконец,

рассматриваемая прямая непременно содержит все идеальные точки, так как мы хотим, чтобы она имела одну общую точку со всякой обыкновенной прямой. Итак, прямая, о которой идет речь, неизбежно должна обладать как раз всеми теми свойствами, которыми мы наделили идеальную прямую в нашей плоскости.

Согласно принятым условиям, каждая бесконечно удаленная точка определяется или представляется семейством параллельных прямых, точно так же как иррациональное число определяется последовательностью «вложенных» рациональных отрезков. Такого рода условный способ описывать параллельность с помощью терминов, первоначально предназначенных для интуитивно отличных объектов, единственной своей целью имеет сделать излишним перечисление исключительных случаев; эти последние теперь автоматически покрываются теми же терминами (и оборотами речи), которые первоначально употреблялись для «обыкновенных» случаев.

Резюмируем: наши условия, касающиеся бесконечно удаленных элементов, были выбраны таким образом, чтобы законы, регулирующие отношение инцидентности между обыкновенными точками и прямыми, сохранялись и в расширенной области, чтобы операция нахождения точки пересечения двух прямых, ранее возможная только в случае непараллельности, могла быть выполнена без ограничений. Соображения, которые привели нас к формальному упрощению в отношениях инцидентности, способны показаться несколько абстрактными. Но читатель убедится на следующих страницах, что они будут вполне оправданы результатами.

2. Идеальные элементы и проектирование. Введение бесконечно удаленных точек и бесконечно удаленной прямой на плоскости позволит нам гораздо более удовлетворительным образом рассмотреть проектирование одной плоскости на другую. Пусть плоскость p проектируется на плоскость p′ из центра O (рис. 83). Эта проекция устанавливает соответствие между точками и прямыми p и точками и прямыми p′. Каждой точке A на p соответствует единственная точка A′ на p′ со следующими исключениями: если выходящий из O проектирующий луч параллелен плоскости p′, то он пересекает p в точке A, которой не соответствует никакая обыкновенная точка плоскости p′. Такие исключительные точки плоскости p расположены на прямой l, которой не соответствует никакая обыкновенная прямая плоскости p′. Но оговаривать эти исключения становится излишним, если мы условимся точке A сопоставлять бесконечно удаленную точку на плоскости p′, взятую в направлении прямой OA, а прямой l — сопоставлять бесконечно удаленную прямую в плоскости p′. Аналогично, некоторую бесконечно удаленную точку в плоскости p мы сопоставляем каждой точке B′ на такой прямой m′ в плоскости p′, через которую