12.2. Закони теплового випромінювання. Індуковане випромінювання. Лазери.

Потужність випром. з одиниці площі поверхні тіла в одиничному інтервалі частот наз. випромінювальною здатністю тіла. Якщо потужність випром. в інтервалі частот (ν,ν+dν) з одиниці площі позначити через dW, то випром. здатність E(ν,T)=dW/dν – спектральна густина поверхневого випромінювання.

Під поглинальною здатністю тіла розуміють відношення к-ті поглинутої тілом Е до загальної T падаючого випром. Тіла, що здатні поглинати всі падаючі на них промені довжини хвилі при Т, наз. абсолютно чорними тілами (АЧТ).

Правило Прево: якщо два тіла поглинають різну к-ть Е, то і випром. буде різним. Кіргоф встановив к-сний зв’язок між випром. і поглин. здатністю тіл. Згідно закону Кіргофа відношення випром. і поглин. здатностей тіла є універсальною для всіх тіл ф-цією частоти і Т. Ф-ція Кіргофа не залежить від природи тіл. Якщо випром. здатність АЧТ позначити через ε(ν,Т), оскільки А(ν,Т)=1, отримаємо: Е(ν,Т)/А(ν,Т)=ε(ν,Т)/1=ε(ν,Т). Отже універсальна ф-ція Кіргофа це випром. здатність АЧТ

Закон Стефана-Больцмана: інтегральна (просумована по всіх частотах) випром. здатність тіл ~ 4 степені абсолютної Т:

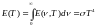σ=5,672*10^-12 Вт/см²град⁴

Закон Віна: закон Стефана-Больцмана хоч і визначає вид залежності Е(Т), але не дає ніяких відомостей про частотну залежність Е випром.. Він визначив характер залежності Е(ν,Т): Е(ν,Т)=αν³F(ν/Т), де α – постійна величина, F – деяка ф-ція, вигляд якої Віну був невідомий. Правило зміщення, встановлене Віном, говорить: довжина хвилі, яка відповідає mах випром. здатності, обернено ~ абсолютній Т. Можна визначити довжини хвиль, на які припадають максимуми Е випром. при різних Т. При Т<4000 К mах знах. в області ІЧ випром. При Т=5000 К mах відповідають жовто-зеленому кольору. При Т>6000 К mах зміщується в область УФ випром. mах випром. здатність ~ 5 степені Т АЧТ: Е_max=αТ⁵.

Закон Релея-Джинса: Релей застосував закони стат. фізики до випром. і отр. залежність E(ν,T) ~ ν²kT, де k – стала Больцмана. Джинс провів точні розрахунки і встановив:

– ф-ла Релея-Джинса.

«УФ катастрофа». Ф-ла Релея-Джинса співпадає з експериментом в області малих частот і великих температур. Отримати закон Стефана-Больцмана з ф-ли Релея-Джинса неможливо,

!!!

+17.2 *вимушене випром. і лазери !*

6.Поляризація світла. Подвійне променезаломлення.

7.Дифракція світла. Принцип Гюйгенса-Френеля. Дифракційна гратка.

. Дифракція світла. Принцип Гюйсена-Френеля. Дифракція на круговому отворі.

Явище відхилення світла від прямолінійного поширення в область геометричної тіні наз. дифракцією світла. Це явище випливає із принципу Гюйсенса:

• кожна точка хвильового фронту є джерелом вторинних хвиль.

Френель доповнив принцип Гюйсена.

• кожна точка хвильового фронту є джерелом вторинних хвиль і будь-яка точка у фронті хвилі є когерентною з іншою точкою в цьому фронті.

Останнє твердження носить назву принципу Гюгенса-Френеля.

Розглянемо дифракцію на круглому отворі.

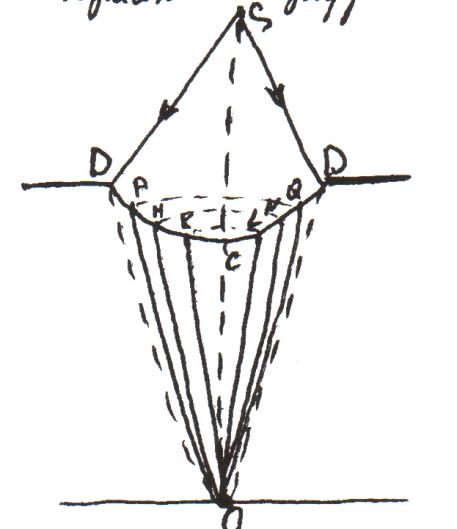Світло проходить через отвір DD на еран.

Для того, щоб розрахувати розподіл світла в точці О, викор. допоміжні прийоми. Проведемо із точки О конічні поверхні до перетину з поверхнею сферичної хвилі DСD. Довжини виберемо так, щоб відстань від точок C,L,N,Q…. до точки О зростала на довжину півхилі λ/2. Поверхня хвилі DСD розіб’ється на кільцеві зони. Площадки цих зон майже однакові, бо ОС›› λ/2, але дія в точці О буде різною. Дійсно, різниця ходу до точки О між будь-якою точкою першої зони і другої буде λ/2, тому світлові хвилі, дійшовши до точки О будуть послаблятися. Тобто в точці О дія першої зони практично знищується дією другої зони. Аналогічні твердження покажуть, що дія третьої зони протилежна дії другого, четверта протилежна третій і т.д. взагалі кажучи дії сусідніх зон Френеля майже знищують одна одну.

Якщо отвір DD такий, що в ньому поміщається дві зони, то в т. О майже не буде світла, більша частина світла розсіється навколо т. О, так що ми побачимо меншу пляму з світлим кільцем навколо неї. Якщо ж число зон 3, то третя зона послаблює другу і в т.О падає світло від першої зони. Ми побачимо світлу пляму з чорним кільцем навколо неї.

Взагалі кажучи, при парному числі зон в центрі буде темна пляма, охоплена світлими і темними кільцями, що чергуються. При не парному числі зон буде протилежна картина.

8.Класична форма випромінювача. Спектральний склад випромінювання. Лоренцова форма і ширина ліній випромінювання.

Розгл. випром. атома на основі моделі лго. Нейтральний атом можна представити у вигляді сукупності гармонічних осциляторів (диполів, які коливаються). Це пов’язано з тим, що випром. ізольованого атома еквівалентне випром. сукупності гармонічних осциляторів.

Найпростіший випадок – коли атом у вакуумі (ε=μ=1, v=с) скл. з одного електрона і одного (+) заряду. Якщо (+) заряд вважати нерухомим, а радіус-вектор електрона, який здійсн. гармонічні коливання позначити 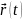, то р-ня руху електрона буде: , де m – маса електрона, α – коеф. квазіпружності. Розв’язок буде , де .

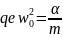Таке зміщення електрона з зарядом q відносно положення рівноваги ств. дипольний момент:

Диполь, що коливається є джерелом сферичної ел. магн. хвилі, вектори напруженості якої на великих відстанях від джерела рівні по величині і взаємно перпендикулярні. Нехай радіус-вектор проведений у точку спостереження складає кут θ з напрямком дипольного моменту .

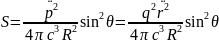– миттєве значення потоку ел.магн. Е, що випром. у напрямку θ. Випром.виходить із центра диполя.

З останніх формул можна зробити наступні висновки:

1) При θ=0 (тобто вздовж диполя), Н=Е=0, отже, S=0, тобто диполь не випром. ел. магн. Е в напрямку своєї осі. 2) При θ=π/2, Е=Е_max, отже S=S_max, тобто max значення випром. буде по напрямку, перпендикулярному осі диполя. 3) При θ=const, E=H~1/R, тобто хвиля, що випром. осцилятором є сферичною. Інтенсивність випром.:

Щоб заряжена частинка випром. ел.магн. хвилі, вона повинна рухатися з прискоренням 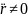. Цей висновок є вірним при умові v<с. Якщо частинка рухається зі υ>с, то вона випром. ел.магн. Е навіть при рівномірному прямолінійному русі (ефект Вавілова-Черенкова).

Інтенсивність періодично змінюється, тому доцільно визначити середню інтенсивність випром. осцилятора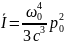

, де w₀ – Е осцилятора при е=0. Е лго зменшується по експоненціальному закону. - час життя осцилятора (час протягом якого Е осцилятора зменшується в е раз).

Під спектром в оптиці розуміють сукупність частот монохроматичних коливань, якими можна представити світло джерела. Графічності по частотам (або довжинам хвиль). Спектр випром.атома:

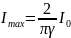
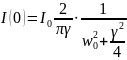
Г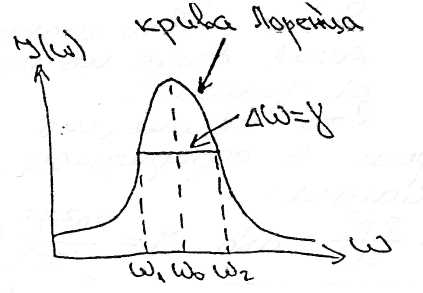 рафік залежності І(w) наз. контуром спектральної лінії.

Контур спектральної лінії наз. природним, якщо він обумовлений тільки затуханням внаслідок випромінювання. Відповідно ширина спектральної лінії у цьому випадку називається природною шириною. Ширину спектральної лінії прийнято характеризувати шириною контура при значенні інтенсивності: .

Тоді: → .

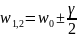Отже, ширина спектральної лінії по шкалі частот рівна:

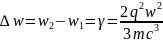
Отже, природня ширина спектральної лінії гармонічного осцилятора рівна константі затухання (оберненому часу життя осцилятора). Для видимого світла (λ=5000Å) ∆w~10⁸ с^-1. Формула (14) описує найменше з значень ∆w. В реальних умовах різні фактори приводять до затухання коливань і відповідно, до розширення спектральних ліній. Наприклад, ширина, обумовлена зіткненнями осциляторів, а також ефектом Доплера.

Наявність природної ширини спектральних ліній випливає і з квантової теорії. Розширення спектральної лінії, згідно квантової теорії, пояснюється тим, що енергетичні рівні мають деяку ширину ∆w, величина якої визначається співвідношенням невизначеності Гейзенберга: ∆wτ~h, де τ- час життя атомів на енергетичному рівні шириною ∆w. Тоді ∆w~h/τ, тобто природна ширина спектральних ліній обернено пропорційна часу життя атома в початковому стані.