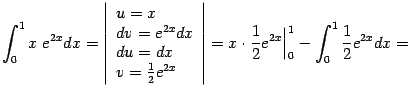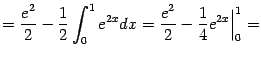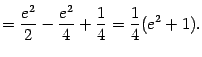23.Формула замены переменной (интегрирование подстановкой).

Метод замены переменной (интегрирование подстановкой)

ТЕОРЕМА. Пусть 1) функция   непрерывна на промежутке  ; 2) функция   непрерывно дифференцируема на промежутке  , имеет множество значений, принадлежащих промежутку  , и    на  . Тогда

,  (**)

где   – какая-либо первообразная для функции   на  ;

    – обратная функция для функции  .

В самом деле, условие   гарантирует существование  обратной функции    и ее производной  . Дифференцируя по   на   сложную функцию  ,   и учитывая  равенство  , получим

.

Итак, функция   – первообразная для   на  .

Теорема показывает, что если при вычислении интеграла   удается подобрать функцию  ,   с указанными свойствами и интеграл   вычисляется, то исходный  интеграл определяется формулой (**), при этом счет проводится по алгоритму:

выбрать функцию   с непрерывной и знакопостоянной  производной так, чтобы эта функция отображала промежуток   в промежуток определения функции  ; найти обратную  функцию  ;

найти  ,  ;

заменить интеграл   интегралом  ;

вычислить  ;

вернуться к первоначальной переменной интегрирования  ,  заменяя  . Получить ответ в виде  .

Ниже рассмотрены некоторые часто встречающиеся интегралы и применяемые для их вычисления подстановки.

1. Тригонометрические подстановки  ,  ,   применяются в тех случаях, когда подынтегральное  выражение содержит радикалы  ,  ,   или их степени.

ПРИМЕР 1. Вычислить  .

РЕШЕНИЕ. Положим  ,  . Тогда  ,  ,  ,  . Имеем 

, отсюда получаем

.

ПРИМЕР 2. Вычислить  .

РЕШЕНИЕ. Положим  ,  . Тогда  ,  ,  ,   и

.

Возвращаясь к первоначальной переменной   (пункт 5 алгоритма), выразим сначала   через  :

.

Отсюда  .

24. Интегрирование по частям определённого интеграла.

Формула интегрирования по частям для определённого интеграла.

 Пример  Вычислим интеграл

Выгодно взять  и  , так что получаем:

При этом возникший по дороге внеинтегральный член 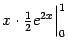 мы вычислили так:

    

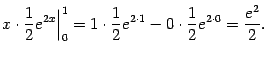
Особенно ясно проявляется указанное в замечании преимущество в том случае, если формулу интегрирования по частям приходится применять несколько раз подряд. Равномерное приближение непрерывной функции тригонометрическими и алгебраическими многочленами. 2-ая теорема Вейерштрасса. Интеграл Фурье и его свойства.

Преобразование Фурье, понятие об обратном преобразовании Фурье. Аналог признака Дини (без доказательства). Синус и косинус- преобразования Фурье.

25.Несобственные интегралы. Интеграл от неограниченной функции.

Определение несобственного интеграла от неограниченной функции.  Особенность на левом конце промежутка интегрирования. Пусть функция f(x) определена на полуинтервале (a, b], интегрируема по любому отрезку  , и имеет бесконечный предел при  . Несобственным интегралом от f(x) по отрезку [a, b] называется предел 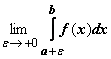 . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.  Примеры: 17. 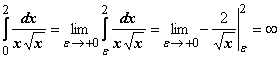  - интеграл расходится;  18.     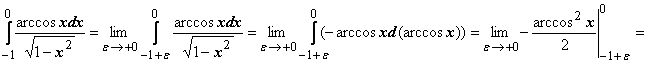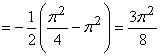- интеграл сходится.

Применение формулы Ньютона-Лейбница. Если для функции f(x) на полуинтервале (a, b] существует первообразная F(x), то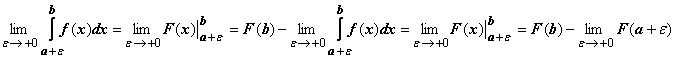 , и сходимость интеграла определяется наличием или отсутствием конечного предела  . Будем писать просто  , имея в виду, что если соответствующий предел конечен, то интеграл сходится, в противном случае - расходится.  Примеры: 19.   (интеграл сходится).  20.   (интеграл расходится).  В следующих дальше случаях неограниченности функции будем поступать аналогично.

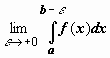Особенность на правом конце промежутка интегрирования. Пусть функция f(x) определена на полуинтервале [a, b), интегрируема по любому отрезку  , и имеет бесконечный предел при  . Несобственным интегралом от f(x) по отрезку [a, b] называется предел  . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.

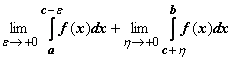Особенность во внутренней точке промежутка интегрирования. Пусть функция f(x) определена на отрезке [a, b], имеет бесконечный предел при стремлении аргумента к какой-либо внутренней точке c этого отрезка:  , интегрируема по любому отрезку, не содержащему точку c. Несобственным интегралом от f(x) по отрезку [a, b] называется  . Интеграл сходится, если оба эти пределы существуют и конечны, в противном случае интеграл расходится.

Несколько особенностей на промежутке интегрирования. Этот случай сводится к предыдущим. Пусть, например, функция имеет бесконечные пределы при стремлении аргумента к внутренним точкам c₁, c₂, c₃ отрезка [a, b] (a < c₁ < c₂ < c₃ < b) и правому концу b, и интегрируема по любому отрезку, не содержащему эти точки. Тогда несобственный интеграл определяется как  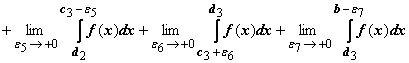  . Здесь d₁, d₂, d₃ - произвольные точки, удовлетворяющие неравенствам a < c₁ < d₁ <c₂ < d₂ < c₃ < d₃ < b. 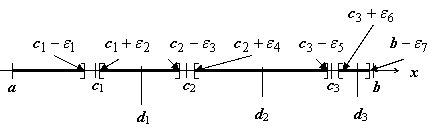 Пример: 21.  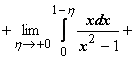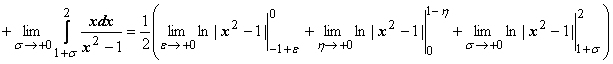   , и интеграл расходится, так как все три предела бесконечны. Решение с применением формулы Ньютона-Лейбница: 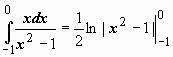  - расходится, так как первообразная  обращается в бесконечность в точке x = -1.

Признаки сравнения для неотрицательных функций. Как и для несобственных интегралов первого рода, для интегралов второго рода вводится понятие абсолютной сходимости, позволяющее в ряде случаев свести исследование сходимости интегралов от произвольных функций к исследованию сходимости интегралов от неотрицательных функции, и рассматриваются признаки сравнения для таких интегралов. Ввиду того, что принципиальная сторона вопроса изучена на случае интегралов первого рода, кратко перечислим основные факты. Будем предполагать, что подынтегральная функция имеет особенность на левом конце промежутка интегрирования.  Признак сравнения. Пусть функции f(x) и g(x) интегрируемы по любому отрезку   и при x > aудовлетворяют неравенствам  . Тогда:  если сходится интеграл  , то сходится интеграл  ;  если расходится интеграл  , то расходится интеграл    В качестве "стандартного" интеграла, с которым сравнивается данный, и в этом случае обычно берётся интеграл от степенной функции типа 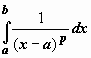 . Этот интеграл сходится, если p < 1, и расходится, если  : 

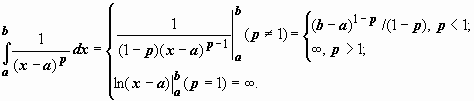
Признак сравнения в предельной форме. Пусть неотрицательные функции f(x) и g(x) интегрируемы по любому отрезку  и пусть существует конечный  . Тогда несобственные интегралы   и   сходятся или расходятся одновременно.  Сравнение интеграла   со "стандартным" интегралом   в предельной форме даёт правило: если при  неотрицательная функция f(x) - бесконечно большая порядка роста ниже первого по сравнению с  , то   сходится; если f(x) имеет порядок роста единица или выше, то интеграл расходится. Примеры:  22. 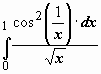 . Так как при  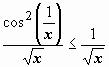  , и интеграл от большей функции сходится, то данный интеграл сходится;  23. 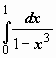 . При       , p = 1, интеграл расходится;  24. 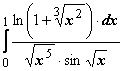 . 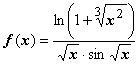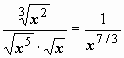При       ,  , интеграл расходится;  25. 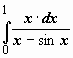 . При       , интеграл расходится.  Абсолютная и условная сходимость несобственных интегралов от разрывных функций определяется аналогично тому, как это было сделано для несобственных интегралов по бесконечному промежутку ( 12.1.4) , а именно: несобственный интеграл от неограниченной функций   называется абсолютно сходящимся, если сходится интеграл  , и условно сходящимся, если интеграл  сходится, а интеграл   расходится (если сходится  , то   тоже обязательно сходится).  Пример: Исследовать на сходимость интеграл:  26. 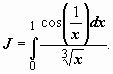  Так как 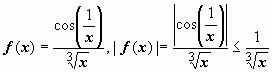 , то исходный интеграл сходится абсолютно.

• При отсутствии абсолютной сходимости установить условную сходимость можно с помощью признаков Абеля и Дирихле: 

Признак Дирихле. Интеграл 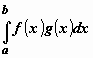  сходится, если:  1).функция f(x) непрерывна и имеет ограниченную первообразную на (a, b];  2).функция g(x) непрерывно дифференцируема и монотонна на (a, b], причём .

Признак Абеля. Интеграл   сходится, если:  1).функция f(x) непрерывна на (a, b] и интеграл   сходится;  2).функция g(x) ограничена, непрерывно дифференцируема и монотонна на (a, b], то есть имеет конечный предел: .