53.Теорема о среднем значении. Сведение двойных интегралов к повторным.

Теорема о среднем, значении Если функция f(x; у) непрерывна на области Р, то существует такая точка (а; b)   Р , что

где S_p - площадь области Р. Сведение двойных интегралов к повторным Теорема 1. Пусть Р - плоская область, ограниченная графиками непрерывных функций g(x) и h(x), таких что g(x)   h(x), х   [а; b], и, быть может, отрезками прямых х = а и x = b. Если функция f(x; у) непрерывна в области Р, то

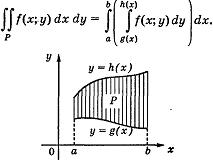
Интеграл, стоящий в правой части формулы, называется повторным интегралом и записывается в виде

Отметим, что если плоская область Р ограничена графиками непрерывных функций g(y) и h(y), таких что g(y)   h(y), у   [с; d], и, быть может, отрезками прямых у = с и у = d, то порядок интегрирования может быть иным

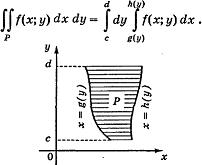
Замечание. Расчет двойных интегралов приводит к необходимости вычисления выражений  , в которых интегрирование ведется по переменной у, а переменная х при этом играет роль константы (как, впрочем, и любое выражение р(х), зависящее только от х). Пусть

тогда

Аналогичным образом осуществляется интегрировала ние выражений вида

54. Замена переменных в двойных интегралах.

При вычислении интегралов часто бывает удобно сделать замену переменных , где  - непрерывны в некоторой области . Впоследствии мы будем часто писать просто вместо и т.п. и, кроме того, говорить при выполнении вышеупомянутых условий, что и - непрерывно дифференцируемые в функции.

Пусть при этом формулы  задают взаимно-однозначное отображение областей: . Кроме того, не стремясь к минимальности условий, потребуем, чтобы всюду на области

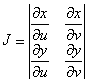 не равнялся 0.

Теорема 1.При сформулированных выше условиях для непрерывной на D функции  справедливо .

Пример 6

Используя необходимую замену переменных, найти объем, ограниченный сверху  , снизу - осью Оx, на параллелограмме с вершинами (0,0), (1,1), (2,0), and (1,-1)

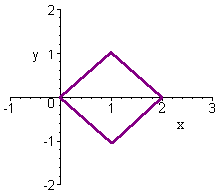
Решение

Найдем уравнения четырех прямых, составляющих параллелограмм

или 

Область задана следующими неравенствами:

и .

Произведем замену переменных:

,

Матрица Якобиана:

.

Область задана неравенствами:

и ,

а функция   уравнением  .

Получаем двойной интеграл:

.

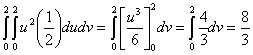55. Тройные интегралы.56.Сведение к повторным.57.Замена переменных

Тройные интегралыПринципиальное отличие тройных интегралов от двойных состоит в том, что теперь появляется еще одна (третья) переменная интегрирования. Во всем остальном они схожи. Как и в случае двойных интегралов, основными методами вычисления тройных интегралов является сведение их к повторным и замена переменных в подынтегральных выражениях.

58. Интегрирование непрерывной функции по неограниченной области.

66. Формула Грина и её применение.

Т: Предположим, что является правильной областью, которая ограничена гладкой кривой . В функции непрерывны вместе с частными производными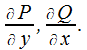  В этом случае имеет место формула Грина:

 

 

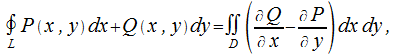
следует также отметить, что в положительном направлении обходится кривая .

Обратимся к выражению . Допустим, что является уравнением кривой , а есть уравнение кривой , (рис. 26.4). Следовательно

 

 

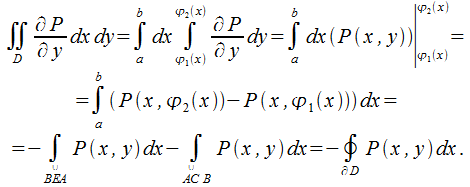
Произведя подобную операцию по отношению к кривым  получим

 

 

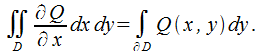
В результате вычитания предыдущего равенства из вышеобозначенного, составляется формула Грина.

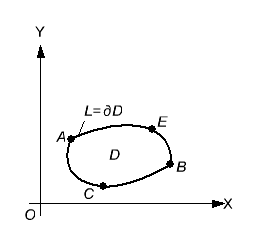Рис. 26.4

 Замечание. При условии, что область - неправильная, формулу можно назвать справедливой, поскольку подается делению на правильные элементы, а также представляется возможным использование формулы Грина к каждому из них, при этом применяются свойства 3⁰ для двойных интегралов и криволинейных интегралов II рода.