8.Асимптоты графика функции.
Асимптотой к кривой называется прямая, к которой график функции неограниченно приближается.
Асимптоты:
Вертикальные
Наклонные
Горизонтальные - (частный случай наклонной асимптоты)
I. Вертикальные
асимптоты всегда имеют уравнение 
,
где
–
точка разрыва второго рода.
Значит 
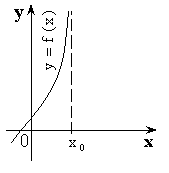
II. Наклонная
асимптота имеет вид 
.
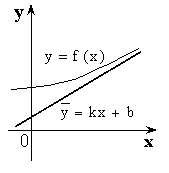
Пример:
–
вертикальная асимптота,
т.к. 
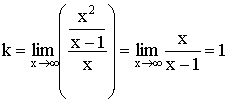
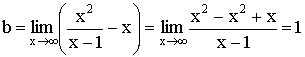
Наклонная
асимптота 
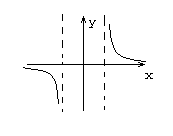
Возможный вариант графика функции.
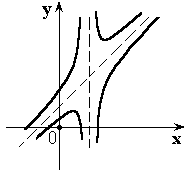
9.Анализ свойств функции, и её построение.
Область определения функции; область значений функции (если это возможно).
2) Промежутки положительных и отрицательных значений функции. Координаты точек пересечения с осями Ох и Оу. 3) Исследование функции на четность, нечетность. 4) Исследование функции на периодичность. 5) Исследование функции по первой производной: - промежутки монотонности; - точки экстремумов; экстремумы функции. 6) Исследование функции по второй производной: - промежутки выпуклости вверх и выпуклости вниз; - точки перегиба. 7) Анализ области непрерывности. Анализ точек разрыва. Асимптоты графика функции. 8) Расчет координат дополнительных точек (если это необходимо). 9) Построение графика функции. Рекомендуем следующую последовательность анализа свойств функции. 1) Область определения функции; область значений функции (если это возможно). 2) Промежутки положительных и отрицательных значений функции. Координаты точек пересечения с осями Ох и Оу. 3) Исследование функции на четность, нечетность. 4) Исследование функции на периодичность. 5) Исследование функции по первой производной: - промежутки монотонности; - точки экстремумов; экстремумы функции. 6) Исследование функции по второй производной: - промежутки выпуклости вверх и выпуклости вниз; - точки перегиба. 7) Анализ области непрерывности. Анализ точек разрыва. Асимптоты графика функции. 8) Расчет координат дополнительных точек (если это необходимо). 9) Построение графика функции.
10.Неопределённый интеграл.
Неопределенным
интегралом от 
называется
класс всех первообразных для
.
- подынтегральная функция.
-
дифференциал.
-
переменная интегрирования.
Для любой непрерывной функции существует первообразная.
Основные тождества.
1.
2.
3.
11. Свойства неопределённого интеграла.
-
линейность
12.Методы интегрирования (метод разложения).
Замена переменных под знаком неопределенного интеграла.
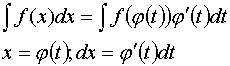
Интегрирование по частям.
Доказательство:
(формула
дифференцирования произведения).
(интегрируем
обе части равенства)
(использование
основного тождества)
(что и требовалось доказать).
Пример:
1) (замена переменной)
2) (интегрирование по частям)
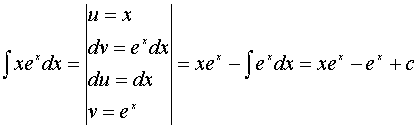
Дополнительный материал
Интегрирование рациональных дробей. Простейшие дроби и их интегрирование.
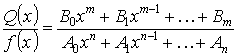
Все коэффициенты действительные числа.
m , n – целые числа.
Нет общих корней.
Если 
, то
дробь называется неправильной, если 
, то
дробь называется правильной.
Если
дробь неправильная, то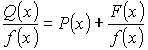 
,
где 
-
правильная дробь; 
-
многочлен.
Простейшие дроби:
1.
2.
, 
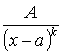и
целое число.
3.
(
в знаменателе неприводимый квадратный
трехчлен).
4.
, 
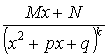и
целое число.
=
=
=
=
=
=
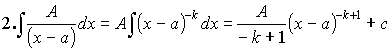
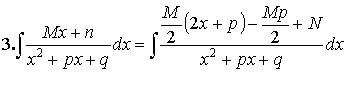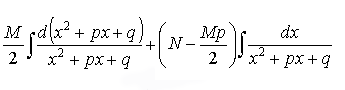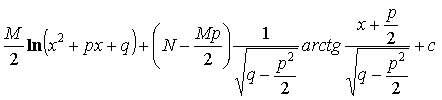
Разложить рациональные дроби на простейшие.
Теорема. Если х = а – корень знаменателя f(x) кратности k , то
Доказательство:
;
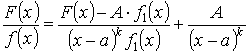(1)
Будем
подбирать А так,
чтобы 
По
теореме Безу это возможно, если
Тогда 
Подставим
в (1)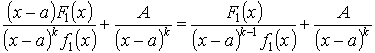 
Следствие:
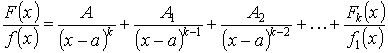
Теорема. Если 
(
-
неприводимый ква дратный трехчлен. 
),
то
Доказательство:
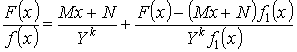
Подберем M и N так,
чтобы числитель делился на Y :
- по
теореме Безу.
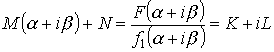
M и N можно найти из этой системы всегда.
Следствие: всякая правильная рациональная дробь может быть разложена в сумму простейших дробей.
Пример:
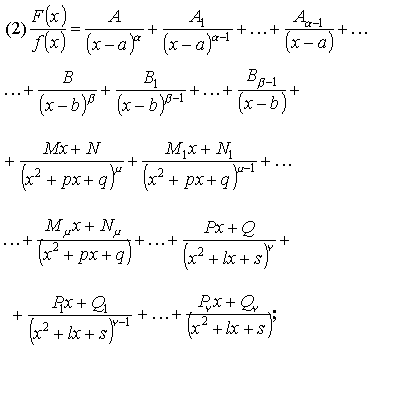
Метод неопределенных коэффициентов.
Правую часть равенства (2) надо привести к общему знаменателю и приравнять в числители коэффициенты при одинаковых степенях F(x). Решая полученную систему уравне ний можно определить все коэффициенты.
Интегрирование рациональных дробей.
Выделить целую часть дроби.
Разложить знаменатель на множители.
Представить в виде суммы простейших дробей.
Найти неопределенные коэффициенты.
Интегрировать каждую простейшую дробь.
Интегрирование иррациональных функций
5.1. 
k
– общий знаменатель дробей 
-
рационализирующая подстановка.
Пример:
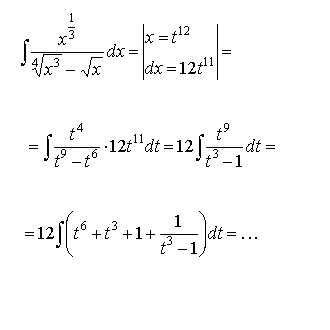
5.2.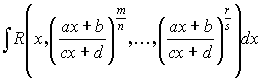 
k – общий знаменатель дробей
Пример:
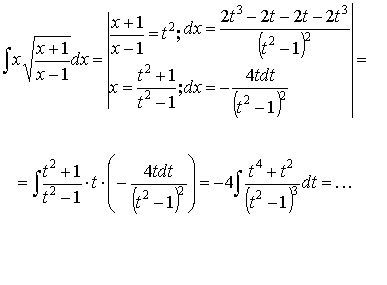
5.3. Тригонометрические подстановки.
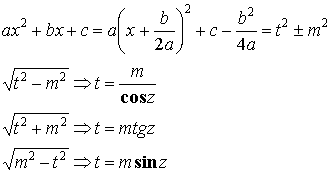
Пример:
-
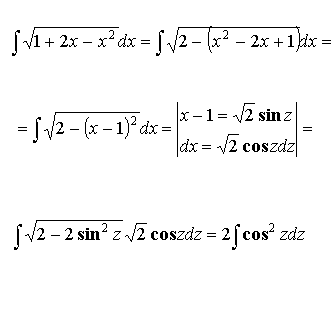
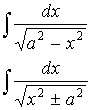обратные гиперболические функции.
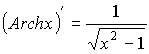
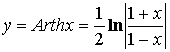
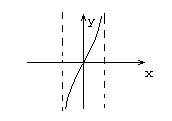
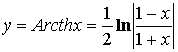
