10.4 Условия Коши-Римана
Условия Коши-Римана дают необходимые и достаточные условия существования производной у функции комплексной переменной.
Пусть
дана функция комплексной переменной
,
у которой
в точке
существует
производная 
.
Тогда в
этой точке выполнены соотношения
,
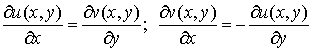которые
и называются условиями Коши-Римана.
Если функции
и
дифференцируемы в
точке 
то
эти условия достаточны для
существования
.
10.5 Интеграл от функции комплексной переменной
Пусть – функция комплексной переменной z и C – некоторая кривая на плоскости z (см. рис. 10.4).
Рис. 10.4 К построению интеграла от функции комплексной переменной
Разобьем
всю кривую на кусочки точками 
так,
что начало кривой есть точка 
,
а конец – точка 
.
На каждом кусочке произвольным образом
выберем среднюю точку 
и
составим интегральную сумму
.
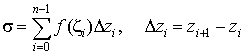Пусть 
.
Если существует 
и
этот предел не зависит от способа
разбиения кривой С на
кусочки и от способа выбора средней
точки, то он называется интегралом от
функции
по
кривой С:
.
Важнейшее неравенство на этот интеграл имеет вид
,
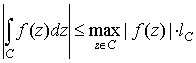где 
есть
длина кривой С.
Теорема. Если
аналитична
в односвязной области G,
то 
по
всем кривым С,
лежащим в G,
зависит только от начала и конца кривой
и не зависит от вида этой кривой.
10.6 Интегральные формулы Коши
Приведем две основные формулы, касающиеся аналитических функций.
Теорема
1. Пусть
аналитична
в односвязной области G.
Тогда для любой точки 
имеет
место формула
,
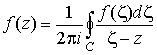где C – любой простой контур, лежащий в G и охватывающий z. В частности, в качестве контура С может быть взята граница области G.
Эта теорема устанавливает очень интересное свойство аналитической функции: ее значения на границе области полностью определяют ее значения внутри области.
Теорема 2. Если аналитична в односвязной области G, то в этой области у нее существуют производные всех порядков, причем
,
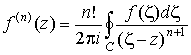где C – любой простой контур, лежащий в G и охватывающий z. В частности, в качестве контура С может быть взята граница области G.
Эта теорема устанавливает еще одно очень интересное свойство функций комплексной переменной, не имеющее аналога для функций вещественной переменной: существование первой производной гарантирует существование всех остальных производных.
Неравенство
Коши. Обозначим
через 
минимальное
расстояние от точки z до
контура С,
и пусть 
.
Тогда имеет место неравенство
,
которое также носит имя Коши.
Определитель
[править]
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Определитель (значения).
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.
Определитель матрицы А обозначается как: det(A), |А| или Δ(A).