10.1.3 Тригонометрическая форма комплексного числа.

         С геометрической интерпретацией связана и еще одна форма записи комплексных чисел, называемая тригонометрической формой их записи.

         Соединим точку (x, y) с началом координат отрезком прямой. Длина этого отрезка r называется модулем комплексного числа z и обозначается | z | или mod(z).

         Угол , который этот отрезок образует с осью ОХ, называется аргументом комплексного числа z и обозначается arg(z).

         Из рисунка ясно, что имеют место соотношения

,

или наоборот

.

Теперь мы можем записать  или окончательно

.

Эта форма и получила название комплексного числа в тригонометрической форме.

         Операции над комплексными числами в тригонометрической форме.

         Пусть имеются два комплексных числа   и  .

         Умножение.

         Легко вывести, что

,

то есть при перемножении комплексных чисел их модули перемножаются, а аргументы – складываются.

         Деление.

         Можно вывести, что

,

то есть при делении комплексных чисел их модули делятся, а аргументы – вычитаются.

         Возведение в степень.

         Пусть  . Тогда имеет место формула

,

то есть при возведении в степень модуль возводится в эту степень, а аргумент –  умножается на нее.

         Извлечение корня.

         Пусть снова  . Тогда имеет место формула

,

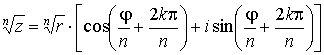с  . Таким образом, корень n-й степени из комплексного числа имеет ровно n различных значений.

         10.1.4 Формула Эйлера. Показательная форма комплексного числа.

         Одна из важнейших формул математического анализа – формула Эйлера – имеет вид

.

С учетом тригонометрической формы комплексного числа его теперь можно представить в виде

,

или, с учетом того, что аргумент определяется с точностью до 2,

  .

Эта форма записи помогает, например, определить логарифм комплексного числа

  .

         10.2 Функция комплексной переменной

         Представим себе, что есть две плоскости комплексной переменной, одна – плоскость комплексной переменной  , другая – плоскость комплексной переменной   (см. рис. 10.2).

         Правило, которое каждой точке z из некоторой области G ставит в соответствие точку w, называется функцией комплексной переменной и обозначается  .

Рис. 10.2 К определению функции комплексной переменной

         Подчеркнем, что и аргумент z и значение функции w – комплексные переменные. Так как   и  , то задание   сводится фактически к заданию двух функций   и   от двух переменных x и y, то есть  .

         Основные понятия теории функций – предел функции, непрерывность функции и соответствующие им теоремы переносятся на функции комплексной переменной. Отличия начинаются в понятии производной.

10.3 Производная от функции комплексной переменной

         Пусть задана функция  . Говорят что у   существует производная в точке z, если существует

.

         Определение. Если   имеет производную в каждой точке области G, то она называется аналитической  в области G.

         Выясним геометрический смысл производной. Рассмотрим на плоскости z бесконечно малый отрезок, соединяющий точки z и z. Тогда длина этого отрезка есть |z|, а arg z  есть угол, который этот отрезок образует с осью OX (см. рис. 10.3).

         Аналогично, на плоскости w бесконечно малый отрезок, соединяющий точки w и w. Тогда длина этого отрезка есть |w|, а arg w  есть угол, который этот отрезок образует с осью OU.

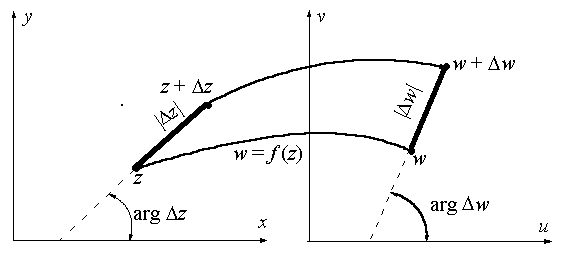
Рис. 10.3 Геометрический смысл производной от функции комплексной переменной

         А теперь вспомним, что  ,  , так что  . Тогда получим

.

Отсюда

.

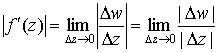Отношение   есть отношение длин отрезков   и  . Таким образом,   есть коэффициент растяжения бесконечно малого отрезка при его отображении с плоскости z на плоскость w.

         Далее, так как

,

то   есть угол поворота бесконечно малого отрезка при его отображении с плоскости z на плоскость w. Заметим, что этот угол поворота не зависит от  , то есть от направления отрезка  .