
- •Однородные системы
- •[Править]Пример
- •[Править]Неоднородные системы
- •[Править]Пример
- •Ранг системы векторов. Базис системы векторов
- •Алгоритм Гаусса для нахождения ранга и базиса системы векторов
- •Линейная независимость
- •[Править]Пример
- •[Править]Определение
- •[Править]Свойства
- •[Править]Значение
- •Подкольцо
- •Комплексное число
- •Определения
- •Стандартная модель
- •Матричная модель
- •Замечания
- •Действия над комплексными числами
- •Геометрическая модель
- •Связанные определения
- •Модуль и аргумент
- •Сопряжённые числа
- •Представление комплексных чисел Алгебраическая форма
- •Тригонометрическая и показательная формы
- •Формула Муавра и извлечение корней из комплексных чисел
- •История
- •10.1 Комплексные числа
- •10.1.1 Алгебраическая форма комплексных чисел
- •10.1.3 Тригонометрическая форма комплексного числа.
- •10.3 Производная от функции комплексной переменной
- •10.4 Условия Коши-Римана
- •10.5 Интеграл от функции комплексной переменной
- •10.6 Интегральные формулы Коши
- •Определитель
- •[Править]Определение через разложение по первой строке
- •[Править]Определение через перестановки
- •[Править]Альтернативные методы вычисления
- •[Править]Свойства определителей
- •[Править]Алгоритмическая реализация
- •2. Деление с остатком. Теорема Безу
- •Неприводимый многочлен
- •[Править]Определение
- •[Править]Свойства
- •[Править]Примеры
- •[Править]Связанные определения
- •[Править]Примеры
- •[Править]Свойства
- •[Править]История
- •Трисекция угла
- •[Править]Построения с помощью дополнительных средств
- •[Править]Трисекция угла при помощи невсиса
2. Деление с остатком. Теорема Безу
Деление с остатком
Определение. Пусть ![]() и
и ![]() — многочлены,
— многочлены, ![]() .
Будем говорить, что
поделен
на
с
остатком, если
представлен
в виде
.
Будем говорить, что
поделен
на
с
остатком, если
представлен
в виде ![]() ,
где
,
где ![]() и
и ![]() —
многочлены, причем
—
многочлены, причем ![]() .
.
Полином называется остатком от деления на , — неполным частным.
Пример. ![]() .
.
![]() .
.
Теорема. (о
делении с остатком). Пусть
и
—
полиномы над полем ![]() ,
.
Тогда существуют единственные
многочлены
и
над
полем
такие,
что
,
.
Тогда существуют единственные
многочлены
и
над
полем
такие,
что ![]() и
.
и
.
Доказательство. Существование.
Пусть ![]() .
Положим
.
Положим ![]() .
.
![]() .
.
Предположим,
что теорема верна не для любого
полинома
(
фиксируем).
Среди всех многочленов
,
для которых теорема неверна, выберем
многочлен наименьшей степени и обозначим
его ![]() :
:
![]()
Пусть ![]() .
Положим
.
Положим
![]()
Коэффициент
при ![]() в
многочлене
в
многочлене ![]() равен
равен ![]() .
Следовательно,
.
Следовательно, ![]() .
Значит, для многочлена
теорема
верна. Существуют такие
.
Значит, для многочлена
теорема
верна. Существуют такие ![]() и
,
что
и
,
что ![]() .
Тогда
.
Тогда

Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.
Единственность.
Предположим, что

1) ![]() .
Значит,
.
Значит, ![]() ,
,
2) ![]() .
.
![]() Получили
противоречие. Этот случай невозможен.
Получили
противоречие. Этот случай невозможен.
Теорема Безу
Теорема. Остаток
от деления многочлена ![]() на
многочлен
на
многочлен ![]() равен
равен ![]() .
.
Доказательство. Степень остатка меньше 1, следовательно, остаток — константа. Пусть — остаток.
![]()
Это
равенство верно при любых значениях ![]() .
Положим
.
Положим ![]() :
:
![]()
Задачи.
1. Проверьте, выполняются ли условия:
1) ![]() делится
на
делится
на ![]() ;
;
2) ![]() делится
на
делится
на ![]() .
.
2. Докажите, что
![]() делится
на
делится
на ![]() .
.
3. Найдите
значения параметров ![]() и
и ![]() ,
при которых
,
при которых
![]() делится
на
делится
на ![]() .
.
4. Найдите все значения параметров и , такие, что остаток от деления
![]() на
равен
на
равен ![]() .
.
5. Найдите
все натуральные ![]() ,
такие, что
,
такие, что
![]() делится
на
делится
на ![]() .
.
6. Известно,
что остаток от деления полинома ![]() на
равен
2, от деления
на
на
равен
2, от деления
на ![]() равен
1. Найдите остаток от деления
на
.
равен
1. Найдите остаток от деления
на
.
7. Найдите
остаток от деления многочлена ![]() на
на ![]() .
.
8. Полином с целыми коэффициентами принимает значение 5 в пяти различных целых точках. Может ли он иметь целый корень?
Неприводимый многочлен
[править]
Материал из Википедии — свободной энциклопедии
Неприводимый многочлен — многочлен, неразложимый на нетривиальные (неконстантные) многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов.
[Править]Определение
Неприводимый
многочлен над полем
― многочлен ![]() от
переменных
над полем
является
простым элементом кольца
от
переменных
над полем
является
простым элементом кольца ![]() ,
то есть, непредставим в виде произведения
,
то есть, непредставим в виде произведения ![]() ,
где
,
где ![]() и
―
многочлены с коэффициентами из
,
отличные от констант.
и
―
многочлены с коэффициентами из
,
отличные от констант.
Многочлен называется абсолютно неприводимым, если он неприводим над алгебраическим замыканием поля коэффициентов. Абсолютно неприводимые многочлены одной переменной ― это многочлены 1-й степени и только они. В случае нескольких переменных существуют абсолютно неприводимые многочлены сколь угодно высокой степени — например, любой многочлен вида
![]()
абсолютно неприводим.
[Править]Свойства
Кольцо многочленов факториально: любой многочлен разлагается в произведение неприводимых многочленов, причем это разложение определено однозначно с точностью до постоянных множителей.
Над полем вещественных чисел любой неприводимый многочлен одной переменной имеет степень 1 или 2, причем многочлен 2-й степени неприводим тогда и только тогда, когда он имеет отрицательный дискриминант.
Над любым полем алгебраических чисел существуют неприводимый многочлен сколь угодно высокой степени; например, многочлен
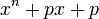 ,
где
,
где 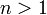 и
―
некоторое простое число, неприводим в
силу критерия
Эйзенштейна.
и
―
некоторое простое число, неприводим в
силу критерия
Эйзенштейна.Если
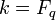 — конечное
поле из
элементов,
а
—
натуральное число, то существует хотя
бы один неприводимый многочлен степени
n из
— конечное
поле из
элементов,
а
—
натуральное число, то существует хотя
бы один неприводимый многочлен степени
n из 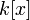 .
.Предположим ― целозамкнутое кольцо с полем частных (например
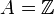 и
и 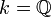 )
и
)
и 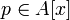 ―
многочлен одной переменной со старшим
коэффициентом 1, тогда
в
,
причем
и
имеют
старший коэффициент 1, то
―
многочлен одной переменной со старшим
коэффициентом 1, тогда
в
,
причем
и
имеют
старший коэффициент 1, то 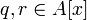 .
.Редукционный критерий неприводимости. Пусть задан гомоморфизм областей целостности
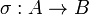 .
Если степень многочлена
.
Если степень многочлена 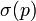 совпадает
со степенью многочлена
и
неприводим
над полем частных области
совпадает
со степенью многочлена
и
неприводим
над полем частных области 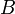 ,
то не существует разложения
,
где
,
то не существует разложения
,
где 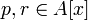 и
отличны от константы.
и
отличны от константы.Например, многочлен со старшим коэффициентом прост в
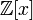 (и,
следовательно, неприводим в
(и,
следовательно, неприводим в 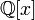 ),
если прост многочлен
,
полученный из
редукцией
коэффициентов по модулю простого
числа.
),
если прост многочлен
,
полученный из
редукцией
коэффициентов по модулю простого
числа.
