1.

Пусть функция     определена в точке     и некоторой ее окрестности. Придадим аргументу приращение   такое, что точка   попадает в область определения функции.  Функция при этом получит приращение   . 

     ОПРЕДЕЛЕНИЕ 1. Производной функции     в точке   называется предел отношения приращения функции в этой точке к приращению аргумента  ,  при  (если этот предел существует и конечен), т.е.

.

Обозначают: .

Производной функции   в точке  справа (слева) называется

(если этот предел существует и конечен).

Обозначают:    – производная y=f(x)  в точке справа,

  – производная y=f(x) в точке слева.

 

1) Физический смысл производной.

Если  функция y = f(x) и ее аргумент x являются физическими величинами,  то производная   – скорость изменения переменной y относительно переменной x в точке .  Например, если S = S(t) – расстояние, проходимое точкой за время t,  то ее производная  – скорость в момент времени .  Если  q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени  t,  то   – скорость изменения количества электричества в момент времени , т.е. сила тока в момент времени .

2) Геометрический смысл производной.

Пусть   – некоторая кривая,  – точка на кривой  .

Любая прямая, пересекающая   не менее чем в двух точках называется секущей.

Касательной к кривой  в точке   называется предельное положение секущей   ,  если точка   стремится к  ,  двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке  существует, то она единственная

Рассмотрим кривую y = f(x)  (т.е. график функции  y = f(x)).  Пусть в точке  он имеет невертикальную касательную  .  Ее уравнение: (уравнение прямой, проходящей через точку и имеющую угловой коэффициент  k).

По определению углового коэффициента  , где  – угол наклона прямой   к оси  .

Пусть  – угол наклона секущей к оси ,  где   . Так как   – касательная, то при 

 ⇒   ⇒     .

Следовательно,

.

Таким образом, получили, что – угловой коэффициент касательной к графику функции y = f(x) в точке (геометрический смысл производной функции в точке).  Поэтому уравнение касательной к кривой y = f(x) в точке можно записать в виде

2.

Определение Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A·Δx+α(Δx)·Δx, где A -- некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е. limΔx→0α(Δx)=0.

 

Теорема Для того, чтобы функция y=f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы она в этой точке имела конечную производную. Доказательство  Необходимость. Предположим: функция дифференцируема в точке x0, т.е. Δy=A·Δx+α(Δx)·Δx. Разделив обе части данного равенства на Δx, получим: ΔxΔy=A+α(Δx). Из определения производной функции в точке: y/(x0)=limΔx→0ΔxΔy=limΔx→0(A+α(Δx))=A.

Т.е. получили, что существует конечная производная функции в точке x0 и y/(x0)=A. Достаточность. Пусть существует конечная производная y/(x0)∈R . Покажем дифференцируемость функции. y/(x0)=limΔx→0ΔxΔy.

Если функция f(x) имеет конечный предел b при Δx→0 , то ее можно представить: f(x)=b+α(x) (α(x)→0) . Исходя из этого: ΔxΔy=y/(x0)+α(Δx), где limΔx→0α(Δx)=0, Δy=y/(x0)·Δx+α(Δx)·Δx→ A=y/(x0) . Теорема доказана.

 

Определение. Дифференциалом функции y=f(x) в точке x0 называется главная линейная относительноΔx часть приращения функции Δy в данной точке.

3.

ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ

Пусть нам известно значение функции y₀=f(x₀) и ее производной y₀' = f '(x₀) в точке x₀. Покажем, как найти значение функции в некоторой близкой точке x.

Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x₀)·Δx.

Т.к., по определению, Δy = f(x) – f(x₀), то f(x) – f(x₀)≈f'(x₀)·Δx.

Откуда

f(x) ≈ f(x₀) + f'(x₀)·Δx

4.

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной: 

y/(x)=limΔx→0ΔyΔx

Δy=f(x+Δx)−f(x). 

Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈  прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0. 

 

 

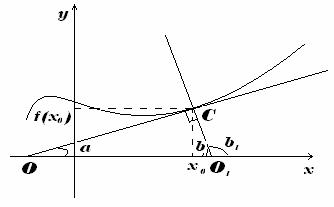
Уравнение нормали

Нормаль -- это перпендикуляр к касательной (см. рисунок). Исходя из этого:

tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали -- это угол β1, то имеем:

tgβ1=tg(π−β)=−tgβ=−1f/(x).

Точка (x0,f(x0))∈  нормали, уравнение примет вид:

y−f(x0)=−1f/(x0)(x−x0).

5.

Теорема (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство. Пусть функция у=f(x) дифференцируема в точке х₀. Дадим в этой точке аргументу приращение х. Функция получит приращение у. Найдем  .

.

Следовательно, у=f(x) непрерывна в точке х₀.

Следствие. Если х₀ – точка разрыва функции, то в ней функция не дифференцируема.

Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.

Пример. у=|х| , х₀=0.

 

            

 

 

 

 

х>0,              ;

х<0,              .

В точке х₀=0 функция непрерывна, но производной не существует.

6.

"Двухслойная" сложная функция записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.  Если f и g - дифференцируемые функции, то сложная функция   также дифференцируема по x и ее производная равна

Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! 

7.