13(30)Потоки в сетях.

Функциональное назначение большинства физически реализованных сетей состоит в том, что они служат носителями системы потоков, в которых объекты текут, движутся или транспортируются по системе каналов с ограниченной пропускной способностью.

(Пример: потоки автомобильного транспорта по сети автодорог; потоки электрического тока в электросети и т. д.)

Ограниченная пропускная способность означает, что интенсивность перемещения предметов по каналу ограничена сверху определенной величиной.

Пусть G=(V,E,Ω) – сеть. Наиболее часто в сети решается задача о max потоке и min разрезе, при этом граф должен удовлетворять условиям:

1. G – связный граф без петель.

2. Существует ровно 1 вершина не имеющая предшествующих (источник) = s.

3. Существует ровно 1 вершина не имеющая последующих (сток) = t.

4. Каждой дуге (v_i, v_j) ϵ E поставлено в соответствие неотрицательное число c (v_i, v_j) ϵ Ω наз. Пропускной способностью дуги.

1. Сеть удовлетворяющая условиям 1-4 наз. Транспортной сетью.

2. В ершины транспортной сети отличные от источника и стока наз. промежуточными.

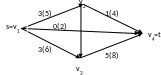
(рис. 1)

v₁ = s - источник

v₄ = t - сток

v₂, v₃ – промежуточные

D f:3 Функция от ϕ(v_i, v_j)определенная на множестве дуг сети G=(V,E,Ω)наз. потоком если ϕ(v_i, v_j)≥0, но ≤ c (v_i, v_j) (v_i, v_j) ϵ E и ∑ ϕ(v_i, v_j) = ∑ ϕ(v_i, v_j) , v_i ϵ V, v_i не ϵ {s, t}

Последнее условие наз. условием сохранения потока: Сумма потоков по дугам заходящих в v_j равна сумме потоков по дугам исходящих из v_j.

Т. об. в промежуточных вершинах потоки не создаются и не исчезают.

П ример: на рис. 1 показан поток в транспортной сети, при каждой дуге указана величина потока по ней. Выполнено 2 условие из Df: и ∑ ϕ(v_i, v_j) = ∑ ϕ(v_i, v_j)

3. Величина ∆(v_i, v_j)= c (v_i, v_j)- ϕ(v_i, v_j) наз. остаточной пропускной способностью дуги (v_i, v_j).

4. Поток наз. полным если любой путь из s в t содержит по крайней мере одну насыщенную дугу.

5. В еличина потока ϕ сети G наз. величина ϕ равная сумме потоков по всем дугам заходящим в t, или равна сумме потоков по всем дугам исходящих из s. ϕ = ∑ ϕ(v_i, t) = ∑ ϕ(s, v_i)

6. П оток ϕ – max если его величина ϕ принимает max значение по сравнению с другими потоками.

Max поток определяется с помощью одного из основных понятий теории сети – разреза.

Разрез может быть представлен как множество дуг, исключение которых из сети определило бы некоторое множество узлов от сети.

Предположим, что множество вершин сети v разбито на 2 непустых непересекающихся подмножеств:

v = V^I V^II ; V^I V^II =0, где V^I ≠0 , V^II≠0

Df:8 Множество дуг, начало которых лежат в V^I, а концы в V^II наз. неориентированным разрезом.

Df:9 П ропускной способностью разреза наз. сумма пропускных способностей входящих в него дуг. c(V^I V^II)

Теорема: (Форда - Фалкерсона) Для любой сети с 1 источником и 1 стоком величина max потока в сети от источника к стоку = пропускной способности min разреза.

Д-во: Алгоритм Ф.- Ф. построения max потока и min разреза основан на 2 процедурах:

(30)1 процедура:

Предположим, что в сети имеется некоторый поток, пусть нулевой. И есть путь из s в t состоящий из ненасыщенных дуг.

Очевидно, что поток в сети можно увеличить на величину ∆ =min из остаточных пропускных способностей, входящих в этот путь.

Перебирая все возможные пути из s в t и переводя такую процедуру увеличения потока, пока это возможно, получим в результате полный поток, т. е. такой поток для которого путь из s в tсодержит по крайней мере 1 насыщенную дугу.

2 процедура:

Рассмотрим произвольный маршрут из s в t. Дуги образующие этот маршрут делятся на 2 типа: -прямые, ориентированные от s в t; - обратные, ориентированные от t в s.

Пусть существует путь в котором прямые дуги ненасыщенные, а потоки на обратных дугах положительные.

∆₁ – min из остаточных пропускных способностей прямых дуг.

∆₂ – min из величин потоков обратных дуг.

Тогда потоки сети можно увеличить на величину ∆ = min {∆₁ , ∆₂ }. Прибавляя ∆ к потокам на прямых дугах и вычитая ∆ из потоков на обратных дугах. Очевидно, что при этом условие сохранения потока (баланса) для узлов входящих в рассматриваемый маршрут не нарушится.

Если множество обратных дуг не пусто, то при такой процедуре увеличения потока фактического перемещения объектов вдоль рассматриваемого маршрута не происходит. Но эта процедура уменьшает потоки на некоторых дугах, которые, возможно, были насыщены. Образуя таким образом новые пути из ненасыщенных дуг, вдоль которых происходит перемещение потока величины ∆.

Замечание: 1-ая процедура – частный случай второй.

Замечание: В общем случае в сети может быть несколько min разрезов.

Замечание: В ситуациях более сложной сети может быть трудно определить наверняка, что таких путей нет. Это тот случай, когда теорема о min разрезе и max потоке оказывается полезной. Т. к. разрез – множество таких ребер, блокировка которых полностью останавливает поток, то величина любого потока не может превысить величину любого разреза. Т. е. может превысить <=> когда поток max, а разрез min.

Если можно найти разрез со значением = величине потока, то такой поток max, а разрез min.