1(18).Основное понятие теории графов. Определения и разновидности графов. Способы задания графов: аналитический, геометрический, матричный. Изоморфизм графов. Примеры.
Опр:
пусть V не пустое множ-во,
множ-во всех его двухэлементных
подмножеств; E
,
тогда упорядоченная пра(V,E)
– называется графом(неориентированным
графом).
Опр: Элем-ты множ-ва V назы-ся вершинами графа, а эл-ты множества Е – рёбрами графа.
Опр: Граф называется конечным, если V конечно.
Опр: Число вершин графа G=(V,E) наз-ся его порядком.
Опр:
Каждому ребру соответствует двухэлементное
подмнож-во вершин, если подмнож-во {
}
соответствует ребру 
,
то вершины 
и
наз-ся смежными, а ребро 
инцидентно вершинам
и 
;
Вершины
и
наз-ся концевыми вершинами ребра
.
Опр: Если концевые вершины совпадают, то рёбро называется петлёй.
Опр:
Рёбра с одинаковыми концами и вершинами
называются кратными (параллельными)
т.е
={
}
и
=
{
},
то рёбра
и
называются кратными.
Опр: Два ребра наз-ся смежными, если они имеют одну общую вершину.
Опр: Степень вершины графа – это число рёбер инцедентных данной вершины, причём петли учитываются дважды {обозначение: Deg( )}
Опр: Если Deg вершины=0, то вершина наз-ся изолированной, а если =1, то висячей.
Граф удобно изображать в виде рисунков т.е представить графически. Вершины графа изображаются точкой а каждое ребро отрезком (линией соединяющей её инцидентные вершины).
Разновидности графов.
Опр: Граф не содержащий петель и кратных рёбер называется простым (обыкновенным).
О
пр:
Мультиграф – это простой граф с кратными
рёбрами.
- простой; - мультиграф
Опр: Псевдограф – это мультиграф с петлями. – псевдограф
Опр:
Тривиальный граф – это граф состоящий
из одной вершины т.е V={0};
Е=
Опр: Нулевой граф – это граф в котором множество рёбер пусто.
Опр:
Полный граф – это простой
граф, в котором каждая пара вершин смежна
(обозначается 
,
где n
число вершин) . 
.
|----|
,
О
пр:
Правильный граф (однородный) – это граф
у которого deg
всех вершин равны между собой.
- правильный граф
Опр:
Пусть 
множество упорядоченных пар элементов
V
,
тогда упорядоченная пара (V,A)
наз-ся ориентированным графом (оркграф);
V
– множество вершин оркграфа, а А –
множ-во ориентированных рёбер, которые
называются дугами.
1(18).
Опр: если пара ( ) дуга, то вершины и наз-ся её началом и концом соответственно.
О
пр:
смешанные графы имеют как дуги так и не
ориентированные рёбра.
Опр:
Граф называется двудольным, если
такое разбиение множ-ва его вершин на
две части (доли), что концы каждого ребра
разным частям, если любые две вершины
входящие в разные доли смежны, то граф
называется полным двудольным.
П
олный
двудольный граф доли которого состоят
из р и q
вершины обозначаются 
.
a
d
e
b
c
Способы задания графа.
Аналитический способ задания множ-в V и E.
Геометрический т.е граф изображается графически в виде рисунка из точек и линий.
Любой граф может быть представлен в матричном виде.
Опр: Матрицей
смежности вершин графа G=(V,E)
называется матрица порядка nxn,
где n=|V|
элементы которые 
представляют собой число различных
рёбер инцидентных вершинам 
и 
Пример: Задать граф G=(V,E) матрицей смежности вершин, если граф задан графически.
1 1 1 0 -таблица смежности вершин графа
1 0 2 0
.
1
2 0 0
Рис.1 0 0 0 0
Замечание;deg(
)
(если нет петель при ней), можно определить
так – это сумма всех элементов i
строки если вершина
имеет петлю, то степень
сумма элементов i
строки, но элемент диагонали 
должен быть удвоен.
Опр: Матрица смежности вершин оркграфа G=(V,A) – это матрица по вертикали указывается вершины начала дуги, по горизонтали вершины конца дуги, а на пересечении I строки и j столбца ставят число равное количеству рёбер с началом в вершине и концом
1(18).
Опр: Матрицей (таблицей) инцидентности
G=(V,E)
называется матрица (таблица) порядка
nxm,
где n=|V|,
m=|E|.
По вертикали перечисляются вершины, по
горизонтали рёбра, а на пересечении i
строки и j
столбца ставим 1 если данная вершина
и
ребро 
инцидентны, в противном случае ставим
0.
Пример: Для графа записать таблицу инцидентности.
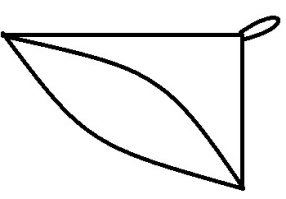
1 0 0 1 1
1 1 1 0 0
. 0 1 1 1 0
0 0 0 0 0
Опр: Матрицей инцидентности оркграфа G=(V,A) это матрица порядка nxm, n=|V|, m=|A| на пересечении i строки и j столбца ставим 0 если дуга и вершина не инцидентны, 1 если вершина является концом дуги и -1 если вершина является началом дуги.
Опр: Список рёбер графа – это таблица состоящая из двух граф, в первой графе указывается рёбра, во второй инцидентные им вершины.
Пример: Для графа заданного на рис.1 задать данный граф списком рёбер.
Опр: Список дуг оркграфа это таблица напротив дуги записываются вершины графа согласно ориентации дуг данного оркграфа.
Опр: Список дуг оркграфа это таблица напротив дуги записываются вершины графа согласно ориентации дуг данного оркграфа.
Изоморфизм графов.
Два
графа 
и
называются изоморфными, если между
множ-ми их вершин существует такое
взаимооднозначное соответствие, при
котором в одном из графов (рёбрами,
дугами) соединены вершины в том и только
том случае, если в другом графе рёбра
(дуги) соединены соответствующие им
вершины. У оркграфа ориентированная
дуга должна быть одинаковой. Отношение
изоморфизма графов является отношением
эквивалентности, т.е обладает св-ми
рефлексивности, транзитивности и
симметричности, т.о мн-во всех графов
разбивается на классы, так что графы из
одного класса изоморфны, а из разных
классов не изоморфны. В силу изоморфности
один и тот же граф может быть изображён
разными диаграммами (рисунками). Ниже
приведен пример одного и того же рисунка.
1(18).
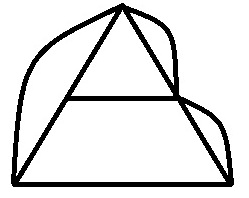
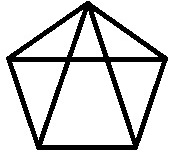
Эти графы изолированы т.к в 3 случаях содержится одна и та же информация о вершинах и рёбрах графа и взаимном расположении.
Опр: Граф G называется помеченным, если его вершинам присвоены некоторые метки.
На рисунке изображены три разных помеченных графа.
2 1 3
1 3 2 3 2 1
Т1. Графы изоморфны
когда их матрицы смежности вершин
получают-я друг из друга одновременными
перестановками строк и столбцов .
Из Т1 следует, что ранги матрицы изоморфных графов равны – это позв-т ввести следующие понятия.
Опр: Рангом графа называется ранг его матрицы смежности вершин.
Т2. Графы (оркграфы) изоморфны когда их матрицы инцидентности получаются друг из друга перестановкой строк и столбцов.