25 Вопрос
PU
y(x)=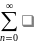
y(0)n/n!*xn
xϵ<-R,R>
(1)
PT y(x)= y(0)n/n!*(x-x0) xϵ<-R,R> (2)
Вычисление значений функций y(x) x=x1. Раскладываем функцию в ряд Тейлора и Маклорена и вычисляем значение функции
Вычисление интегралов.
fn(x0)/n!(x-x0)n=
fn(x0)/n!
(x-x0)ndx=
fn(x0)/n!
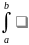(x-x0)ndx=
f(x0)(x-x0)n+1/n!(n+1)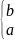
[a,b]
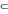<-R,R>
ДУ. a) Линейные ДУ. y’’+p(x)y’+g(x)y=0 Пусть p(x)=
q(x)=
;
y(x)=
(3)
Подставим (3) в и находим коэффициенты
Сn
и находим
из обращения в нуль коэффициентов при
любой степени х в полученном выражении
б)
Если p(x)=
;
q(x)=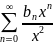
Пусть a0,b0,b1
не равны, о оновр тогда решение уравнения
(1) можно искать в виде обобщённого
степенного ряда y(x)=xs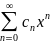
;
ρ(ρ-1)+a0ρ+b0=0
(6)
a0=
,b0=
Если ρ1-ρ2- не целое. y1(x)=xρ1
;
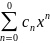y2(x)=xρ2
y00=c1y1(x)+c2xy2(x) (!!!)
б) Если ρ1-ρ2- целое
2.1 Ряд Фурье. Пространство функции l2 [- ]. Определение, св-ва.
Рассмотрим
множество f(x)
:
=
непрерывные на [-
]
Кусочные непрерывные [- ], имеющие кон число точек разрыва 1го рода
Свойства функции:
Если f(x)
L2
, то С*f(x)
L2
Доказательство:
=С2*
<
Если f1(x);f2(x) L2 то f1(x)+f2(x) L2
Д-во:
(f1(x)+f2(x))2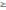
0
f12
f1f2+f22
=>
f12+f22>
f1f2
=
<
<2
Благодаря этим свойствам образуется линейное векторное пространство, которым можно показать, что L2 не имеет конечного базиса. Базис содержит бесконечное множество векторов
Можно ввести скалярное произведение:
{f(x),g(x)}
=
(g(x), f(x)) =
(f(x),g(x)) =(g(x),f(x))
{f1(x)+f2(x),g(x)} =
=
(
+
)*
=
*
+
*
{ f(x), f(x)} = 0
(|f(x)|) =
{|f(x)-g(x)|}=
2(Ряды Фурье). Показать ортогональность функций 1, cosx, sinx, cos2x, sin2x,…,cosnx, sinnx,… на [-π,π].
{1, sinx, cosx, sin 2x, cos 2x, ... , sin nx, cos nx, ...}
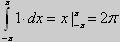Поэтому
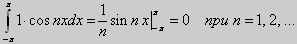
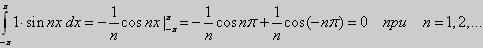
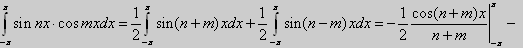
Если n=m,
то
при n ≠ m,
n, m = 1, 2, 3, ... Если n = m, то
Значит,
при n ≠ m, n, m = 1, 2, 3, ... Если n = m, то
То есть
Таким образом, доказано, что система на отрезке [ - π, + π] ортогональная.
Вопрос 3 фурье
5)Ряд Фурье для периодических функций с периодом T=2l
Пусть
f(x)
есть период. ф-я с T=2l,отличным
от 2π. Разложим ее в ряд Фурье. Замена
переменной:
/
Тогда
ф-я
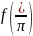будет переод-й ф-й от t
c
T=2π.
Ее можно разложить на
,где
,
Возвратимся
к старой переменной:
Имеем:
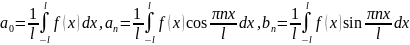
Ряд
Фурье будет иметь вид:
