15 Вопрос.

П-ОЛДУ с постоянными коэффициентами

L(y)=yⁿ+a₁y^n-1+…+a_n-1y’+a_ny=0 (11)

a₁,a_2,…,a_n-const

Метод Эйлера: ищем решение в виде y=e^λx λ-const (12)

y’=λe^λx,y”=λ²e^λx…yⁿ=λⁿe^λx (13)

(12) и (13) в (11)

L(e^λx)= λⁿe^λx+a₁ λ^n-1e^λx+…+a_n e^λx

L(e^λx)= (λⁿ+a₁ λ^n-1+a₂ λ^n-2+…+a_n) e^λx

L(e^λx)=P(λ) e^λx≡0 (14)

e^λx≠0 xϵ(-∞;∞)

Из (14) следует P( λ)≡λⁿ+a₁ λ^n-1+…a_n=0 (15)

Характеристическое уравнение(ху)

Задача. Интегрирование диф. уравнения свелось в

Случаи:

1. ХУ(15) имеет n различных вещественных корней

n решений λ₁, λ₂,.., λ_n y₁= e^λ1x,y₂= e^λ2x,…,y_n= e^λx(16)

W(e^λ1X,…, e^λnX)= e^λ1X e^λ2X … e^λnX

λ₁ e^λ1X x₂ e^λ2X… λ_n e^λnX

………………………

λ₁^n-1 e^λ1X … λ_n^n-1 e^λnX

= e^λ1X* e^λ2X*… e^λnX * I I …. I

λ₁ λ₂ …. λn ≠0 xϵ(-∞;∞)

λ₁^n-1 λ₂^n-1… λ_n^n-1

определитель Вандер Монда т.е (16)-ФСР

Тогда y_оо=с₁y₁+ с₂y₂+…+ с_ny_n= c₁e^λ1X + c₂ e^λ2X+…+ c_n e^λnX (17)

2. Среди корней XУ имеется комплексный корень λ₁=α+iβ

Тогда имеется обязательно сопряжённый корень λ₂=α+iβ

y₁₌ e^α+iβ)x=e^αx(cosβx+isinβx)= e^αxcosβx+ ie^αxsinβx=u(x)+iv(x)=y₁(c волнистой чертой) y₂(c волн.ч)= e^α-iβ=e^αxcosβx-ie^αxsinβx= u(x)+iv(x)

Теорема о комплексном решении ДУ

Пусть y=u+iv – комплексное решение ДУ. Тогда L(y)≡0 следовательно L(u)+iL(v)=0 следовательно

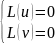
т.е u(x) и v(x)-действительное решение ДУ.

Вывод: двум комплексным сопряжённым корням λ_1,2=α+iβ характеристического уравнения P(λ)=0 соответствует вещественное решение y₁= e^αxcosβx,y₂= e^αxsinβx

3. Среди корней ХУ корень λ₁ кратности “к”

XУ P(λ)=(λ-λ₁)^kQ_n-k(λ)=0 (18)

P ’(λ)=k(λ- λ₁)^k-1 Q(λ)+ (λ- λ₁)^kQ’(λ)

P’’(λ)= k(k-1)(λ-λ₁)^k-2Q(λ)+2k(λ-λ₁)^k-1Q’(λ)+ (λ-λ₁)^kQ’’(λ)

…………………………………………………………….. (19)

P^{(k) (}λ)=k(k-1)…2*1Q(λ)+…+ (λ-λ₁)^kQ^k(λ)

Если λ₁-корень ХУ(18), то (Q(λ₁)≠0)

P(λ₁)≡0 P’(λ₁)=0,P’’(λ₁)=0…,P^k-1(λ₁),но P^k(λ₁)=k’Q(λ₁)≠0

Ранее имеем L(e^λx)=P(λ) e^λx=0 (20)

Продифференцируем соотношение (20) по λ:

(L(e^λx))’_λ=(P(λ) e^λx)’_λ ;(e^λx)’=P’(λ) e^λx+P(λ)x e^λx

L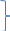 (x e^λx)=P’(λ) e^λx+P(λ)x e^λx

Ещё раз дифференцируем по λ k-2 раз

L(x² e^λx)=P’’(λ) e^λx+2P’(λ)x e^λx+P(λ) e^λxx² (21)

Если в соотношении (21) подставим λ₁-корень ХУ,то будем иметь

L(x e^λx)=P’(λ₁) e^λ1x+P(λ₁)x e^λ1x=см 19=0 L(x e^λ1x)≡0 следовательно x e^λ1x тоже решение ОЛДУ-n. L(x² e^λ1x)=см 19=0+0+0=0 следовательно x² e^λ1x-тоже решение ОЛДУ-n. L(x^k-1 e^λ1x)=0+0+…+0=0 следовательно x^k-1 e^λ1x тоже решение ОЛДУ-n. Вывод: Если λ₁-как кратный корень ХУ, то ему соответствует ,,к,, решений:

y₁= e^λ1x,y₂=x e^λ1x,y₃=x² e^λ1x,…,y_k=x^k-1 e^λ1x –входят в ФСР как лин. независимые

4. Среди корней ХУ имеются почленно сопряжённые как кратные корни λ_1,2=α+iβк р “ к” Всего 2к корней. Следует 2 кратным корнем имеет два вещественные решения y₁= e^αxcosβx,y₂= e^αxsinβx

В силу кратности y₃=x e^αxcosβx,…,y_2k-1=x^k-1 e^αxcosβx

y₄=x e^αxsinβx,…, y_2k=x^k-1 e^αxsinβx

Вопрос 16. Лнду-n с постоянными коэффициентами: отыскание частного решения методом неопределенных коэффициентов по виду правой части специального вида (все случаи доказывать).

(1)

L(y)=0 (2) ОЛДУ-n

(3)

XY: (4)

(5)

1.А 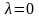- не корень ХУ (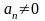 в (1))

y_чн=Q_m(x)=C₀x^m+C₁x^m-1+…+C_m,

y_чн^’=C₀mx^m-1+…+C_m-1=Q^’_m(x), Q^’_m(x)-многочлен степени (m-1)

y^’’_чн=………..=Q^’’_m(x), Q^’’_m(x)-многочлен степени (m-2)

y⁽ⁿ⁾_чн=…..=Q⁽ⁿ⁾_m(x)

(6) и (7) в (1) и приравниваем коэффициенты при одинаковых степенях x в обеих частях получим: (m+1) – алгебраических выражений для определения C₁………

1.Б λ_1,2,3….,s=0-корень ХУ (4) кратности s, тогда уравнение (1) будет иметь вид:

a₀y⁽ⁿ⁾+a₁y^(n-1)+…+a_n-sy^(s)=f(x) (8)

ХУ: a₀λⁿ+a₁λ^n-1+….+a_n-sλ^s=0

λ(a₀ λ^n-s+a₁ λ^n-1-s+…+a_n-s-1)=0

(8)-ДУ-n, допускающие понижение порядка, тип 2⁰

(9)

a₀p^(n-s)+a₁p^(n-s-1)+….+a_n-sp=f(x) НЛДУ-(n-s) порядка

ХУ: a₀ λ^n-s+a₁ λ^n-s-1+….+a_n-s=0 (11)

при чем λ=0 – не корень ХУ (11), тогда по случаю 1.А P_чн=Q_m(x)=C₀x^m+C_m , но P_чн=y^(s)_чн (смотри (9), тогда

y^(s)_чн=Q_m(x) ДУ, допускающее понижение порядка (тип 1)

Достаточно: y_чн=x^sQ_m(x)

2⁰ f(x)=e^αxP_m(x)=e^αx(b₀x^m+b₁x^m-1+….+b_m)

y’’+a₁y’+a₂=e^αxP_m(x) (13)

y=e^αxz(x) (14) λ²+a₁λ+a₂=0 (*)

y’=z’e^αx+αze^αx=e^αx(z’+αz)

z’’=z’’e^αx+2αz’e^αx+α²ze^αx=e^αx(z’’+2αz’+α²z)

(14) в (13) и сокращаем на e^αx:

z’’+2αz’+α²z+a₁(z’+αz)+a₂z=P_m(x)

z’’+(2α+a₁)z’+ (α²+a₁α+a₂)z=P_m(x) (15)

2.А α-не корень ХУ (*)

Тогда в левой части (15) все члены 1.А z_чн=Qm(x)=C₁x^m+C₂x^m-1+…+C_m

yчн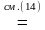 e^αxQ_m(x)

2.B α-корень ХУ (*) кратности 1

α²+a₁α+a₂=0, т.е. в (15) нет члена с z (случай 1.B)

yчн=x¹e^αxQ_m(x)

2.C α-корень ХУ(*) кратности 2, т.е. λ₁= λ₂=α По Теореме виета Þ λ₁+ λ₂= -a₁ , 2 λ₁= -a₁Þ2 λ₁+a₁=0

Þ в (15) не будет z и z’’, по случаю 1.B

z_чн=x²Q_m(x)

y_чн=x²e^αxQ_m(x) (16)

2.D В общем случае. α –корень ХУ(4) кратности s,

y_чн=x^se^αxQ_m(x)=x^se ^αx(C₀x^m+……+C^m) (17)

3⁰ f(x)=e^αx[P_m(x)cosβx+R_k(x)sinβx] (18)

cosβx=

sinβx=

f(x)=f₁(x)+f₂(x)

Известно, если L(y)=f₁(x)+f₂(x) НЛДУ-n

y_чн=y_чн1+y_чн2

Случай 3⁰ свелся к случаю 2⁰

3.A Если α±iβ-не корень ХУ

yчн= , r=наиб{m,k} (19)

3.B Если α±iβ-не корень ХУ кратности S

y_чн= (20)