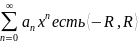- •3 Вопрос.
- •4. Замена переменной в ти (геометрический вывод для общего случая); переход в ти к цилиндрическим и сферическим координатам.
- •7.Криволинейные интегралы 2 рода
- •8.Независимость ки-2 от пути интегрирования. Восстановление функции по ее полному дифференциалу.
- •2. F(X,y), непрерывны в д, тогда для всякого (х0,у0)
- •11. Дифференциальные уравнения высшего порядка: основные понятия и определения. Три типа ду высшего порядка, допускающие понижение порядка.
- •15 Вопрос.
- •Вопрос 16. Лнду-n с постоянными коэффициентами: отыскание частного решения методом неопределенных коэффициентов по виду правой части специального вида (все случаи доказывать).
- •18.Доказать теоремы:
- •Признак Даламбера
- •2) Коши-Радикальный
- •3) Признак Коши-Интегральный
- •21. Знакочередующиеся ряды. Доказать теорему Лейбница.
- •22. Функциональные ряды.
- •25 Вопрос
- •2.1 Ряд Фурье. Пространство функции l2 [- ]. Определение, св-ва.
- •2(Ряды Фурье). Показать ортогональность функций 1, cosx, sinx, cos2x, sin2x,…,cosnx, sinnx,… на [-π,π].
- •Вопрос 3 фурье
2) Коши-Радикальный
Если
в
(an
),
 =L,
то
=L,
то
L<1-ряд сходится
L>1-ряд расходится
L=1-??
Доказательство
=L

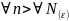 =>
|
=>
|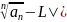 <
<
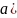 L<1
L<1
=q-L
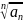 -L<
=q-L
-L<
=q-L
<qn начиная с некоторого номера
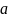 n<qn
n<qn
N<qN
N+1<qN+1
 2
ряда
2
ряда
a1+a2+a3+…aN+aN+1+aN+2+… (6)
qN+qN+1+qN+2+… (7)
начиная
с N
члены (6)<(7) ряд (7) геом прогрессия
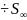 q<1;
=
q<1;
=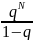 - конечное число, тогда по признаку
сравнения (6) сходится
- конечное число, тогда по признаку
сравнения (6) сходится
Б) L>1 aN+1>aN; aN>1 т.е не выполняется НУС
В) L=1-??
3) Признак Коши-Интегральный
Рассмотрим ряд (an )
a(n)
непрерывная функция на [n0; ]
]
Если
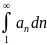 ,
- конечное число, то
–сходится
,
- конечное число, то
–сходится
Если =0, или , то – расходится
=A(n) =
=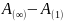
Вопрос 20.Если для последовательности {Sn,n≥1} частичных сумм существует конечны предел S, то ряд называется сходящимся, а число S-суммой данного ряда. Ряд называется расходящимся, если lim Sn (при n→0) не существует или бесконечен.
НУС Для того что бы ΣAn сходился, необходимо, что бы lim An(при n→0)=0
Если ряд сходится то остаток ряда тоже сходиться. Отбрасывание первых членов ряда не влияют на сходимость. Если ряд сходиться то остаток стремиться к нулю.
Т Знакоположительный ряд всегда имеет сумму: А) Если сумма ряда конечна, то ряд сходиться. Б) Если сумма бесконечна, то ряд разходится.
Абсолютная и условная сходимость Ряд ΣA (от 1 до ∞) называется абсолютно сходящимся, если ряд Σ‖A‖ также сходится. Если ряд ΣAn (от 1 до ∞) сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно. Ряд ΣА (от 1 до ∞) называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
21. Знакочередующиеся ряды. Доказать теорему Лейбница.
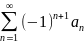 =
a1-a2+a3-a4+…-…+
=
a1-a2+a3-a4+…-…+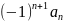 +…
+…
an≥0
Доказать теорему Лейбница
Если
в
(an≥0)
выполняется
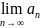 =0,
то
=0,
то
Ряд сходится
S>0
S<a1
Док-во:
S2n= a1-a2+a3-a4+…+a2n-1-a2n+…
S2n= (a1-a2)+(a3-a4)+…+(a2n-1-a2n)+…
≥0 ≥0 ≥0
S2n≥0,
 ≥0
≥0
б) S2n= a1-(a2-a3)-(a4-a5)-…-(a2n-2-a2n-1)- a2n…
S2n≤ a1, ≤ a1
в ) S2n+1= S2n+ a2n+1 0 НУС
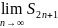 =
+
=
+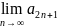
= чтд.
22. Функциональные ряды.
О)
ФР:
 (1) x
Î<a,b>
(1)
(1) x
Î<a,b>
(1)
O)
Если в (1) x=x0,
то
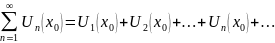 (2) – числовой ряд
(2) – числовой ряд
О)
Если
 – (2) сходится, то говорят, что ФР (1)
сходится в (.) x0
– (2) сходится, то говорят, что ФР (1)
сходится в (.) x0
О) Если – (2) " x0 Î <a,b>, то говорят, что ФР (1) сходится на <a,b>
О) Если - (2) расходится, то ФР (1) расходится в (.) x0
О)
- (2) сходится в (.) x0,
если
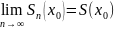
Частичная сумма сумма числового ряда
т.е. " e>0 $ N(e,x0): "(n>N) Þ ½Sn(x0)-S(x0)½<e
!!! N(e,x0) зависит и от e и от x0
Равномерная сходимость.
О)
ФР (1) сходится равномерно на <a,b>,
если "
e>0
$
N(e):
"(n>N)
Þ
½Sn(x)-S(x)½<e
"
“x”
Î
<a,b>
одновременно, где Sn(x)=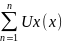 – частичная сумма, S(x)
– сумма ряда
– частичная сумма, S(x)
– сумма ряда
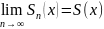
S(x)=Sn(x)+Rn(x)
Rn(x)=Un+1(x)+Un+2(x)+… - остаток ряда
Признак Вейерштрасса равномерной сходимости ФР.
Т)
Если дан ФР
 и
и
 (Cn≥0)
– сходится, при этом ½Un(x)½≤Cn
"
x
Î<a,b>,
то ряд
– сходится равномерно на <a,b>
(Cn≥0)
– сходится, при этом ½Un(x)½≤Cn
"
x
Î<a,b>,
то ряд
– сходится равномерно на <a,b>
Доказательство:
S(x)=Sn(x)+Rn(x)
Rn(x)=S(x)-Sn(x)

Частичная сумма остаток
½Rn(x)½=½Un+1(x)+Un+2(x)+…½≤Cn+1+Cn+2+…≤an<e " n>N(e) т.к. – сходится
½Rn(x)½<e " x Î <a,b> Þ ½Sn(x)-S(x)½<e " x Î <a,b>
Теорема о непрерывности суммы равномерно сходящегося ряда.
Теорема. Сумма ряда непрерывных функций, мажорируемого на некотором отрезке [о, Ь], есть функция, непрерывная на этом отрезке.
Доказательство.
U1(x)+U2 (x)+U3 (x) +… (1)
S(x)=Sn(x)+Rn(x)
Sn= U1(x)+…+Un (x)
Rn(x)= Un+1(x)+Un+2 (x)+…
Возьмем на отрезке [а, b] произвольное значение аргумента х и придадим ему такое приращение Dх, чтобы точка х+Dx лежала тоже на отрезке [a, b].
Введем обозначения:
DS=S(x+Dх)—S(х), DSn = Sn(х +D х)—Sn(х),
тогда
DS=DSn+Rn(x+Dх)-Rn(х),
откуда
|DS| ≤ | DSn | + | Rп(х+Dх) | + | Rn (x) |. (2)
Это неравенство справедливо для любого номера п.
Чтобы доказать непрерывность S(х), нужно показать, что при любом наперед заданном и как угодно малом e > 0 найдется число s > 0 такое, что при всех | Dx | < s будет | DS | < e.
Так как данный ряд (1) мажорируемый, то при любом наперед заданном e > 0 найдется такой номер N, что при всех п ≥ N, будет выполняться неравенство
| RN(x) | < e/3 (3)
при любом х из отрезка [a, b]. Значение х+Dх лежит на отрезке [а, b] и потому выполняется неравенство
| RN(x+Dx) | < e/3. (3')
Далее, при выбранном N частичная сумма SN (х) есть функция непрерывная (сумма конечного числа непрерывных функций) и, следовательно, можно подобрать такое положительное число s, что для всякого Dх, удовлетворяющего условию | Dx | < s, выполняется неравенство ,
| DS(x)| < e/3. (4)
На основании неравенств (2), (3), (3') и (4) получаем
| DS(x)| < e/3 + e/3 + e/3 = e
т. е.
| DS(x)| < e при | Dx | < s,
а это и означает, что S(х) является непрерывной функцией в точке х (и, следовательно, в любой точке отрезка [a, b]).
Замечание. Из доказанной теоремы следует, что если сумма ряда на каком-либо отрезке [а, b] разрывна, то ряд не мажорируем на этом отрезке.
T) (о почленном интегрировании)
Если
ряд сходится равномерно в <a,b>,
то
 ,
где [a1,
x]
Ì
<a,b>
,
где [a1,
x]
Ì
<a,b>
![]()
Доказательство.
S(x)=Sn(x)+Rn(x)

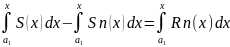
½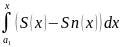 =
=
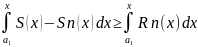
<e (в силу равномерной сходимости)
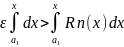
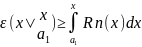

e(b-a)≥
Þ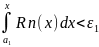
e1
В
итоге
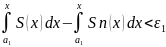 Þ
Þ

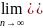

Т) (о почленном дифференцировании)
Пусть:
1) дан
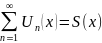 (сходится "
x
Î
<a,b>)
(сходится "
x
Î
<a,b>)
2) Un(x) – непрерывно дифференцируемы в <a,b>, т.е. $ U’n(x) " x <a,b>
3)
 – сходится равномерно в <a,b>
– сходится равномерно в <a,b>
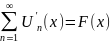 – непрерывная
функция
– непрерывная
функция
Тогда

Доказательство: на теоремы о почленном интегрировании можно почленно интегрировать на [a1, x] Ì <a,b>
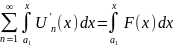
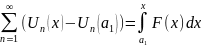
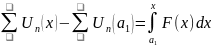
S(x)-S(a1)=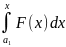
(S(x)-S(a1))’x=
S’(x)=F(x)
S’(x)=F(x)=
23)Степенные ряды, обобщенные степенные ряды: осн. понятия и определения. Обл. сходимости степенного ряда. Доказать теор. Абеля для степ. ряда. Свойства рядов: а)непрерывность суммы степ. ряда; б)о почленном интегрировании; в)о почленном интегрировании.
О
Степенным
рядом наз-ся
функциональный ряд вида
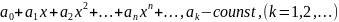
Областью сходимости степ. Ряда явл. некоторый интервал, который, в частности, может выражаться в точку
Т
Абеля Пусть
дан
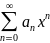 (1)
(1)
А)Если
(1) сх-ся при
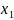 ,
то он сх-ся
,
то он сх-ся
 абсолютно
абсолютно
Б)Если
(1) расх-ся при
 ,
то он расх-ся
,
то он расх-ся

Д-во:
А) Дано:
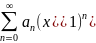 -
сх-ся, т.е.
-
сх-ся, т.е.
 – сх-ся, т.е.
ограничена, т.е.
– сх-ся, т.е.
ограничена, т.е.
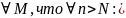
Тогда:
 -
сх-ся
-
сх-ся
 – сх-ся и притом абсолютно
– сх-ся и притом абсолютно
Б)
Дано
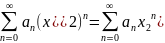 – расх-ся. Пусть
– расх-ся. Пусть
 .
Предположим, что
.
Предположим, что
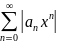 – сх-ся (
– сх-ся (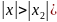 ,
тогда по части (А)
,
тогда по части (А) должен сходиться,что противоречит
условию. Теор. док.
должен сходиться,что противоречит
условию. Теор. док.
Свойства рядов:
Т
Сумма степ. Ряда – непрер-я ф-я в ОС, т.е.
если
 ,
то S(x)-непрер.
в
,
то S(x)-непрер.
в

Т
Степ.
ряд в ОС моно почленно интегрировать и
при этом

Т
Степ.
ряд можно дифференцировать в ОС и при
этом : 1)
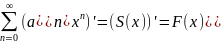 ;
2) OC:
;
2) OC: