8.Независимость ки-2 от пути интегрирования. Восстановление функции по ее полному дифференциалу.

Рассмотрим криволинейный интеграл dy

Пусть = (1) т.е.

- =0

Тогда на основании свойств КИ имеем

+ =0

т.е КИ по замкнутому контуру L

=0 (2)

Таким образом, из условия, что для любых точек M и N КИ не зависит от формы соединяющей их кривой, а зависит только от положения точек, следует, что криволинейный интеграл по любому замкнутому контуру равен нулю

Теорема Пусть во всех точках области D функции Х(х,у) и Y(x,y) вместе со своими частными производными и непрерывны. Тогда для того чтобы КИ-2 по любому замкнутому контуру L, лежащему в области D, был равен нулю, т.е. чтобы

=0, где P= , а Q=

Необходимо и достаточно выполнение равенства

= (3)

Доказательство Рассмотрим произвольный замкнутый конутр L, в области D, и для него напишем формулу Грина:

)dxdy=

Если выполняется (3), то двойной интеграл тождественно равен нулю, и следовательно

=0

Таким образом достаточность доказана

НУ

Если равенство (2) выполняется для любой замкнутой кривой L, в области D, то в каждой точке этой области выполняется (3)

Допустим напротив, что равенство (2) выполняется, т.е.

=0

А условие (3) не выполняется - хотя бы в одной точке. Например в точке Р(x₀,y₀), имеем равенство

- >

Т.к. в левой части неравенства стоит непрерывная функция, то она будет положительна и больше некоторого числа 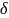>0 во всех точках достаточно малой области G. Содержащей точку Р(x₀,y₀). Возьмем двойной интеграл по этой области от разности - . Он будет иметь положительное значение.

Действительно: 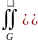)dxdy> dxdy= = G>0

Но по формуле Грина левая часть последнего неравенства равна нулю, что противоречит условию (2), а значит предположение - неверно, отсюда вытекает, что - = во всех точках области D

10. ДУ первого порядка: основные понятия и определения. Теорема о существовании и единственности задачи Коши для ДУ-1(без док-ва)

1. Решение уравнения с разделяющимися переменными

2. Понятие однородной функции n-ого измерения однородные ДУ-1, их решение

3. Линейные ДУ-1: определение, отыскание общего решения методом Бернулли.

4. ДУ-1 Бернулли: определение, отыскание общего решения

Основные понятия и определения

1. Дифференциальным уравнением (ДУ) порядка “n” называется уравнение , связывающее аргумент х, функцию y и ее производные функции.

F(x,y,y',y'',..y⁽ⁿ⁾)=0

2. Старшая производная задана неявно.

3.Порядок старшей производной – порядок ДУ.

4.Если у=у(х), то ДУ- обыкновенное. Если у=у(x,t,ω), то F(x,t,ω, , , )=0-уравнение в частных производных.

5. у=у(х)-решение ДУ, если при подстановке в ДУ получаем тождество.

6. у=у(х,С₁, С₂….С_n) , где С₁, С₂….С_n- произвольные постоянные- общее решение.

7. у=у(х), х=х(у) удовлетворяющее этому ДУ, но не входящие в общее решение- особое решение

8. Если в общем решении у=у(х,С₁, С₂….С_n) произвольным постоянным придать конкретное значение, то имеем частное решение.

9. Отыскание решения - интегрирование ДУ.

10. Если решение ДУ записано через интегралы, то говорят, что решение – квадратуры(даже если интегралы неберущиеся)

Теорема о существовании и единственности задачи Коши для ДУ-1(без док-ва)

у

Д

а)Пусть дано уʹ=f(x,y): 1. Д-область существования f(x,y)