
- •3 Вопрос.
- •4. Замена переменной в ти (геометрический вывод для общего случая); переход в ти к цилиндрическим и сферическим координатам.
- •7.Криволинейные интегралы 2 рода
- •8.Независимость ки-2 от пути интегрирования. Восстановление функции по ее полному дифференциалу.
- •2. F(X,y), непрерывны в д, тогда для всякого (х0,у0)
- •11. Дифференциальные уравнения высшего порядка: основные понятия и определения. Три типа ду высшего порядка, допускающие понижение порядка.
- •15 Вопрос.
- •Вопрос 16. Лнду-n с постоянными коэффициентами: отыскание частного решения методом неопределенных коэффициентов по виду правой части специального вида (все случаи доказывать).
- •18.Доказать теоремы:
- •Признак Даламбера
- •2) Коши-Радикальный
- •3) Признак Коши-Интегральный
- •21. Знакочередующиеся ряды. Доказать теорему Лейбница.
- •22. Функциональные ряды.
- •25 Вопрос
- •2.1 Ряд Фурье. Пространство функции l2 [- ]. Определение, св-ва.
- •2(Ряды Фурье). Показать ортогональность функций 1, cosx, sinx, cos2x, sin2x,…,cosnx, sinnx,… на [-π,π].
- •Вопрос 3 фурье
2. F(X,y), непрерывны в д, тогда для всякого (х0,у0)
х существует решение у=у(х), такое что у(х0)=у0
б) Если решениям ДУ-1 у=у1(х) и у=у2(х) совпадают в одной точке, то они тождественны.
Решение уравнения с разделяющимися переменными
уʹ=f(x)*g(y)
 =
f(x)*g(y) |*
=
f(x)*g(y) |*
 =
f(x)*g(y)*
|/g(y)≠0
=
f(x)*g(y)*
|/g(y)≠0
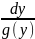 =
f(x)*
=
f(x)*
 =
=
 - общее решение
- общее решение
Понятие однородной функции n-ого измерения однородные ДУ-1, их решение
f(x,y)- однородная измерения m, если f(tx, ty)=tm*f(x, y)
Метод решения однородного ДУ-1:
f(x, y)=f(tx, ty)
уʹ= f(x, y)=f(tx, ty) => уʹ= f(tx, ty)
Пусть
t=
уʹ=
f(
*x,
*y)=f(1,
 )
)
уʹ=
f(1,
) =>однородное ДУ-1 можно сделать
зависимым только от отношения
( )
(5)
)
(5)
=u(x)
y=u(x)*x
уʹ=
= *x+u
(6)
*x+u
(6)
(6) в (5): *x+u= f(1, u) – ДУ-1 с разделяющимися переменными.
Вывод: однородные ДУ-1 подстановкой =u(x) сводятся к уравнению с разделяющимися переменными.
Линейные ДУ-1: определение, отыскание общего решения методом Бернулли.
Если
q(x) 0 для всякого х
0 для всякого х Д, то уʹ+p(x)*y=0-
однородное линейное ДУ-1.
Д, то уʹ+p(x)*y=0-
однородное линейное ДУ-1.
Если q(x) , то уʹ+p(x)*y= q(x)- неоднородное линейное ДУ-1.
общего решения методом Бернулли
у=u(x)*v(x) (10)
=
*v+u*
*v+u* +p(x)*u*v= q(x)

=- p(x)*v |*


v= (11)
(11)
Подставим v в б:
*
=q(x)
|*


 (12)
(12)
Ответ: (11), (12) в (10)
ДУ-1 Бернулли: определение, отыскание общего решения
уʹ+p(x)*y= q(x)*уm|/ уm≠0
m≠0
 +
p(x)*
+
p(x)* = q(x)
= q(x)
= z
 =
=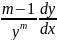 =>
=>
 =>
=>
 +
p(x)*z = q(x)
–НЛДУ-1
+
p(x)*z = q(x)
–НЛДУ-1
Замечание: у=u*v – подстановка.
11. Дифференциальные уравнения высшего порядка: основные понятия и определения. Три типа ду высшего порядка, допускающие понижение порядка.
Основные понятия и определения.
10 ДУ- уравнение связывающее независимую переменную х с искомой функцией y(x) и её производными
 .
.
 (1)
(1)
 (1)
(1)
 (2)
(2)
(1) – ДУ – неразрешённое относительно старшей производной
(2) – ДУ – разрешённое относительно старшей производной y(n) (в нормальном виде)
20 Порядок старшей производной называется порядком ДУ
30 y=y(x), то ДУ называется обыкновенным
40 y=y(x, t, ω)
 -
уравнение в частных производных
-
уравнение в частных производных
50 y=y(x) – решение, если при подстановке ДУ получится тождество
60 y=y(x, C1, C2,…, Cn), где C1, C2,…, Cn – общее решение ДУ-n
70 y=y(x), x=x(y) удовлетворяющие данному ДУ, но не входящие в общее решение, называются особым решением
80 Если в общем решении y=y(x, C1, C2,…, Cn) произвольные постоянные – конкретные значения C1=C01, C2=C02,…, Cn=C0n, то имеем частное решение ДУ
90 Отыскание решений ДУ называется интегрированием ДУ
«решить ДУ», «проинтегрировать ДУ» - синонимы
100 Если решение ДУ записано через интеграл, то говорят, что решение найдено в квадратурах, даже, если эти интегралы не выражены в элементарных функциях
Ф(x, y, C1, C2,…, Cn)=0 – общий интеграл
y=y(x, C1, C2,…, Cn) – общее решение
ДУ-n, допускающие понижение порядка
10 y(n)=f(x)

 -
ДУ-1 относительно y(n-1),
с разделяющимися переменными
-
ДУ-1 относительно y(n-1),
с разделяющимися переменными
d(y(n-1))=f(x)dx
∫d(y(n-1))=∫f(x)dx+C
y(n-1)=∫f(x)dx+C
снова понижаем порядок
 -
ДУ-1 с разделяющимися переменными
-
ДУ-1 с разделяющимися переменными
∫d(y(n-2))=∫(∫f(x)dx+C1)dx+C2
y(n-2)=∫(∫f(x)dx)dx+xC1+C2
 и
т.д.
и
т.д.
20 F(x, y(k), y(k+1),…, y(n))=0 (1)

Нет
явно
 k=1,2,…,n
k=1,2,…,n
k=n случай 10 y(n)=f(x)
 (2)
(2)
 ,…,
,…,
 (3)
(3)
(2) и (3) в (1):
 ДУ-(n-k)
(4)
ДУ-(n-k)
(4)
Замечание: вопрос о решении (4) остался открытым; хорошо, если оно сводится к известным ДУ.
30
 (5)
(5)

Нет явно «х»
Можно понизить порядок на единицу
 (6)
(6)
 =
= =
=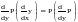
 (7)
(7)

 (8)
(8)
 (9)
(9)
(6)-(9) в (5):

 (10)
(10)
Решение (10)
P=f(y,C1,C2,…,Cn-1) – общее решение (10)
=f(y,C1,C2,…,Cn-1) – ДУ-1с разделяющимися переменными
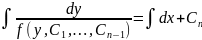 -
общий интеграл ДУ (5)
-
общий интеграл ДУ (5)
12)Линейные ДУ высшего порядка(ДУ-n): однородные, неоднородные. Однородные ДУ-n: доказать теоремы о свойствах решений, понятие фундаментальной системы ЛОДУ-n. Доказать теорему о структуре общего решения ЛОДУ-n.
 (1)
(1)
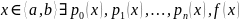

Если
при всех рассматриваемых значениях x
ф-я
 то
уравнение (1) наз-ся линейным
однородным, в
противном сл-е он наз-ся лин-но
неоднородным.
то
уравнение (1) наз-ся линейным
однородным, в
противном сл-е он наз-ся лин-но
неоднородным.
Введем
оператор:
 (2)
(2)
С
помощью оператора (2) ур-е (1) примет вид:
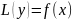
ЛОДУ-(n)
Свойства решений

Т1
Если
 -
решения, то
-
решения, то
 -
тоже решения
-
тоже решения
Д-во:

Тогда:
Т2
Если
 -
решение, то
-
решение, то
 -тоже
решение, где
-тоже
решение, где
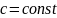
Д-во:
 ,
тогда
,
тогда
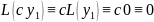
Понятие ФС ЛОДУ-(n)
Т
 опред. на
опред. на
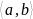 были лин-но незав-мы, необходимо и
достаточно чтобы Вронскиан
были лин-но незав-мы, необходимо и
достаточно чтобы Вронскиан
 хотя бы в одной точке на
хотя бы в одной точке на
Т
Если
Вронскиан
в точке
 ,
то он не равен о ни в одной точке
,
то он не равен о ни в одной точке
О n - лин-но незав-х решений ЛОДУ-(n) наз-ся фундаментальной системой решений (ФСР)
Т о структуре общего решения ОЛДУ-(n)
Если – ФСР ОЛДУ-(n)
, то общ. Решение ОЛДУ-(n) имеет вид:
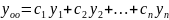 ,
(2)
,
(2)
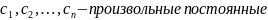
Д-во:
имеем

А)
Тогда

Б) Покажем, что задача Коши имеет единственное решение:
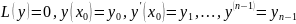 (3)
(3)
(2)
в (3): (4)
(4)
(4) – система лин-х неодн-х алгебр-х ур-й. Она имеет единственное решение, если опред-ль системы не равен 0.

Значит
(4) – единственное решение

Подставляя
найденное значение
 в
(2) получаем решение задачи коши. Теор.
Доказана
в
(2) получаем решение задачи коши. Теор.
Доказана
