
- •3 Вопрос.
- •4. Замена переменной в ти (геометрический вывод для общего случая); переход в ти к цилиндрическим и сферическим координатам.
- •7.Криволинейные интегралы 2 рода
- •8.Независимость ки-2 от пути интегрирования. Восстановление функции по ее полному дифференциалу.
- •2. F(X,y), непрерывны в д, тогда для всякого (х0,у0)
- •11. Дифференциальные уравнения высшего порядка: основные понятия и определения. Три типа ду высшего порядка, допускающие понижение порядка.
- •15 Вопрос.
- •Вопрос 16. Лнду-n с постоянными коэффициентами: отыскание частного решения методом неопределенных коэффициентов по виду правой части специального вида (все случаи доказывать).
- •18.Доказать теоремы:
- •Признак Даламбера
- •2) Коши-Радикальный
- •3) Признак Коши-Интегральный
- •21. Знакочередующиеся ряды. Доказать теорему Лейбница.
- •22. Функциональные ряды.
- •25 Вопрос
- •2.1 Ряд Фурье. Пространство функции l2 [- ]. Определение, св-ва.
- •2(Ряды Фурье). Показать ортогональность функций 1, cosx, sinx, cos2x, sin2x,…,cosnx, sinnx,… на [-π,π].
- •Вопрос 3 фурье
ДИ: задача, приводящая к понятию ДИ; определение ДИ; классы интегрируемых функций; свойства ДИ; вычисление ДИ для прямоугольной области(вывод); для произвольной области(вывод); изменение порядка интегрирования ДИ
Задача, приводящая к ДИ – вычисление объема тела, ограниченного непрерывной ф-й z= f(x, y).
Пусть:
1) в ограниченной замкнутой области D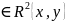 с
площадью s
задана
ограниченная функция f(x,
y);
2)
с
площадью s
задана
ограниченная функция f(x,
y);
2) разбиение области на подобласти Dk
с
площадями ΔDk
и
диаметрами dk,
– диаметр разбиения и
разбиение области на подобласти Dk
с
площадями ΔDk
и
диаметрами dk,
– диаметр разбиения и
 ;
3) зафиксируем точки Mk
;
3) зафиксируем точки Mk
 4)
построим
интегральную сумму
I(dk,Mk)=
4)
построим
интегральную сумму
I(dk,Mk)=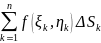 .
О
п р е д е л е н и е .
Конечный предел I
интегральной
суммы In
при
.
О
п р е д е л е н и е .
Конечный предел I
интегральной
суммы In
при
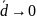 ,
не зависящий от способа разбиения
области D
и выбора точек Mk,
называется двойным
интегралом от
функции f(x,y)
по
области D
и обозначается: In=
,
не зависящий от способа разбиения
области D
и выбора точек Mk,
называется двойным
интегралом от
функции f(x,y)
по
области D
и обозначается: In=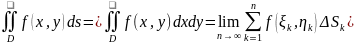
Классы интегрируемых по Риману ф-й:1)непрер-е на D; 2)кусочно-непрер-е, с конечным числом линий и точек разрыва на D (1-го рода)
Свойства
ДИ:
1)
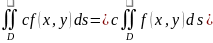
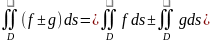
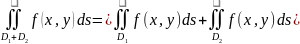
Если m

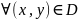 ,
то
ms
,
то
ms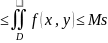 s
– пл-дь D
(теорема об оценке)
s
– пл-дь D
(теорема об оценке) m
m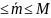 ,
,
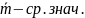
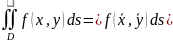 ,
,
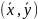 – ср.точка.
(теорема о среднем)
– ср.точка.
(теорема о среднем)
Если f(x,y)
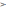 0
0
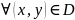 то
то
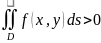
Если f(x,y)
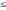 g(x,y)
,
то
g(x,y)
,
то
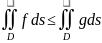
Если

Вычисление ДИ для прям-ой области:
Теорема:
Пусть задана П= ,
и 1)
,
и 1) ;
2)
;
2) ,
тогда
,
тогда
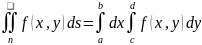
Д


 ок-во:
ym=d
ок-во:
ym=d 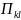
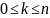
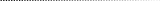







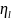

y


 0=c
0=c 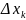

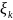
X0=a xn=b
(А)
 ;
;
(В)
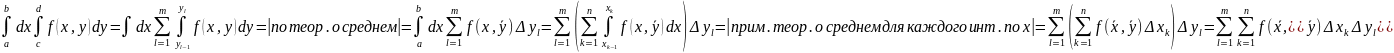 ;
;
Рассмотрим:
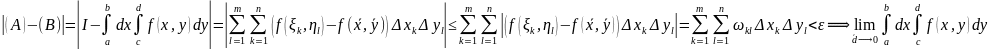
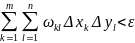 – условие
существования ДИ
– условие
существования ДИ
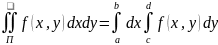
ДИ по произвольной области(ДСК)
Т.
Пусть
задана область,прав-я в направлении ОУ:
1)
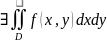 ; 2)
; 2) , Тогда:
, Тогда:
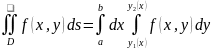
Д-во:
заключим D
в прямоугольник. Введем
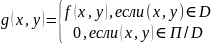
(С)
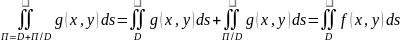
(D)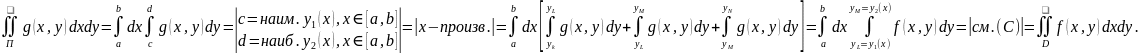
3 Вопрос.
П-Тройной Интеграл
Пусть f(x,y,z) определена в VCR2
V={V1,V2 ,…,Vn} d-диаметр Vi ; Vi-объём Vi
Mi(ƺ,η,ӡ)ϵVn
F(Mi)∆ѵ=
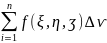
d=наиб{d}
П- Свойства тройного интеграла
Все свойства совпадают со свойствами двойного интеграла
П-Вычисление
а) повторный интеграл
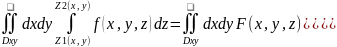
б)
Теорема. Если f(x,y,z)
интегрируема по Риману в области V
Ǝ повторный интеграл (3),то
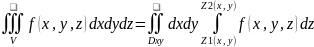
V-правильная в направлении Oz
Замечание:
если V-правильная
в направлении Оx,
то
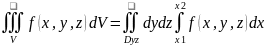
4. Замена переменной в ти (геометрический вывод для общего случая); переход в ти к цилиндрическим и сферическим координатам.
а) переход к цилиндрическим координатам
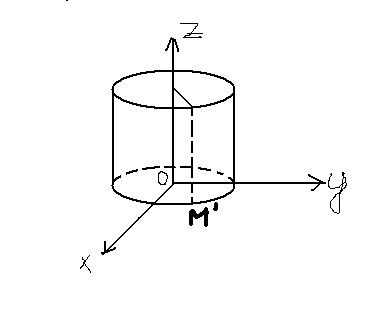 M(x,y,z)=M(ρcos(φ),
ρsin(φ),z)
M(x,y,z)=M(ρcos(φ),
ρsin(φ),z)
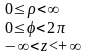 (2)
(2)
(x,y,z)↔( ρ, φ,z)
x= ρcos(φ)
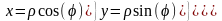 (1)
(1)
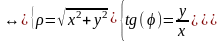 (1’)
(1’)
(2)
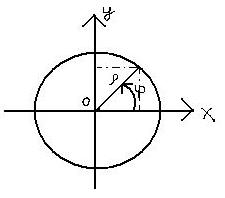
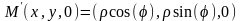

 это
знак якобиана если что;)
это
знак якобиана если что;)
dV=dxdydz=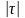 dρdφdz
(3)
dρdφdz
(3)
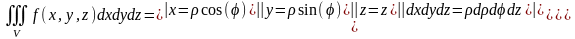
 (4)
(4)
б) Переход к сферическим координатам
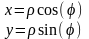
ψ-отсчитывается от Oz по часовой стрелке
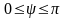
r-радиус-вектор точки M


Пусть
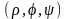 -новые
координаты, тогда:
-новые
координаты, тогда:
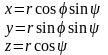 (5)
(5)
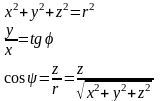
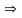
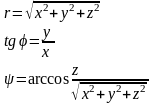 (5’)
(5’)
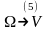
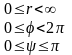
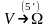
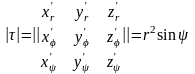
dxdydz=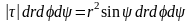
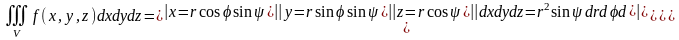
6.криволинейные
интегралы:1)пусть
переменная t
 с помощью отображений x=x(t),y=y(t),z=z(t)
отображает [
с помощью отображений x=x(t),y=y(t),z=z(t)
отображает [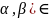 R’
в Г
R’
в Г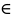
 (1);2)
(1);2)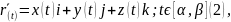 тогда
x(t),y(t),z(t)
– координаты вектор-функции (2) и
определяет некоторую кривую в пространстве
,т.е. x=x(t),
y=y(t),z=z(t),t
тогда
x(t),y(t),z(t)
– координаты вектор-функции (2) и
определяет некоторую кривую в пространстве
,т.е. x=x(t),
y=y(t),z=z(t),t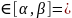 параметр.уравнение
кривой в пространстве.Если t
–время ,то (3)-уравнение траектории
движения.3)если
параметр.уравнение
кривой в пространстве.Если t
–время ,то (3)-уравнение траектории
движения.3)если
 предшествует точке M(
предшествует точке M(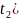 ,
т.е. M[x(
,
т.е. M[x(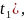 y(
y(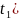 ,z(
]
предшествует M[x(
,z(
]
предшествует M[x(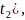 y(
,z(
].
Г:
y(
,z(
].
Г: t)
t)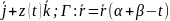 .если
.если

 .если
M(
.если
M( t
t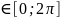 x(0)=x(2
x(0)=x(2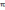 ),y(0)=y(2
)=0.
),y(0)=y(2
)=0.
7.Криволинейные интегралы 2 рода
Определение: Конечный предел интегральной суммы In при λ→∞ ,не зависящий от точек Mi ,называется криволинейным интегралом
второго рода от функций P,Q,R по пути L:
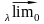 In=
In=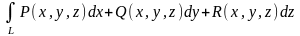
Определение (еще одно хз какое лучше): Если вдоль кривой L определены функции P(M) = P(x, y, z),
Q(M) = Q(x, y, z),
R(M) = R(x, y, z) и существуют интегралы:
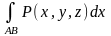 ,
,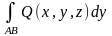 ,
,
 ,то
и их сумму называют криволинейным
интегралом второго рода (общего вида)
и полагают:
,то
и их сумму называют криволинейным
интегралом второго рода (общего вида)
и полагают:
 =
+
+
(1)
=
+
+
(1)
Свойства КИ-2:
1) Если функции P(M), Q(M), R(M) непрерывны на кривой (АВ), то интеграл (1) существует
2) При изменении
направления кривой (то есть перемены
местами начальной и конечной ее точек)
криволинейный интеграл 2-го рода меняет
знак:
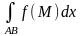 =
-
=
-
Про работу:
Работа при перемещении тела в силовом
поле
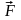 вдоль кривой C выражается
через криволинейный интеграл второго
рода:
вдоль кривой C выражается
через криволинейный интеграл второго
рода:
A=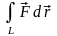 ,
где
− сила, действующая на тело,
,
где
− сила, действующая на тело,
 − единичный касательный вектор (рисунок
1). Обозначение
*
означает скалярное произведение векторов
и
.
− единичный касательный вектор (рисунок
1). Обозначение
*
означает скалярное произведение векторов
и
.
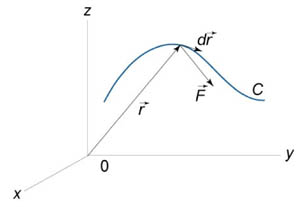
Механически
КИ-2 представляет собой работу переменной
силы
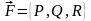 ,
точка приложения которой описывает
кривую L
,
точка приложения которой описывает
кривую L
Вычисление КИ-2 : Если линия AB задана в параметрической форме:x=x(t), y=y(t), z=z(t), t1≤t≤t2, где x(t), y(t), z(t) – непрерывно дифференцируемые функции , и при изменении параметра t от t1 к t2 кривая описывается именно от точки A к точке B, то
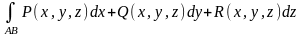 =
=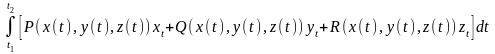
Причем КИ-2 существует, если существует определенный интеграл
