2) «69» Монотонность функции. Признак монотонности

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) > f (x2). Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке. (Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция 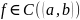непрерывна на (a,b), и имеет в каждой точке производную f'(x). Тогда если 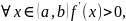то f строго возрастает на (a,b);если 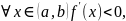то f строго убывает на (a,b).

«70» Точки экстремума функции. Необходимое условие экстремума функции в точке

Если в точке х₀ дифференцируемая функция у=f(х) имеет экстремум, то в некоторой окрестности этой точки выполнены условия теоремы Ферма, и следовательно производная функции в этой точке = 0, т.е. f’(x)=0, но функция может иметь экстремум и в точках, которых она не дифференцируема, так например функция у=х (по модулю) имеет минимум в точке х=0, но не дифференцируема в ней.

Поэтому необходимое условие экстремуму может быть сформулировано следующим образом.

Для того, чтобы функция y=f(x) имела экстремум в точке x₀ ytj,необходимо, чтобы ее производная в этой точке равнялась нулю (f’(x₀)=0) или не существовала.

Точки, в которых выполнено необходимое условие экстремума, т.е производная равна нулю или не существует, называются критическим. Обращаем внимание не то, что эти точки должны входить в область определения функции.

Таким образом, если в какой-либо точке имеется экстремум, то эта точка критическая. Очень важно, однако, заметить, что обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума.

3) 99» Понятие двойного интеграла. Двойной интеграл в прямоугольных декартовых координатах

Двойной интеграл - это обобщение определенного интеграла на двумерный случай. Т.е. для определения понятия двойного интеграла используется функция, зависящая уже от двух переменных: f(x,y). Эта функция должна быть определена на некоторой, обладающей конечной площадью, области D плоскости X0Y. При этом граница области D должна состоять из конечного числа графиков непрерывных функций. Обозначение двойного интеграла.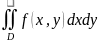

Геометрический смысл двойного интеграла: при неотрицательной функции f(x,y), двойной интеграл по области D представляет из себя объем криволинейного цилиндра, который построен на области D и ограничен сверху поверхностью z=f(x,y).

В декартовых координатах. вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов

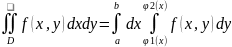
Билет №13

1. «39» Смешанное произведение трех векторов и его основные свойства

2. «76» Понятие первообразной и неопределенного интеграла

3. «117» Теорема о структуре общего решения линейного однородного уравнения высшего порядка

1) Смешанным произведением трёх векторов называют число, равное . Обозначается . Здесь первые два вектора умножаются векторно и затем полученный вектор умножается скалярно на третий вектор . Очевидно, такое произведение есть некоторое число.

Рассмотрим свойства смешанного произведения.

1. Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. .

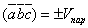Таким образом, и .

2. Для любых векторов 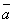, , 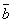справедливо равенство

.

3. При перестановке любых двух сомножителей смешанное произведение меняет знак.

4. Смешанное произведение 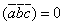тогда и только тогда, когда один из сомножителей равен нулю или векторы – компланарны.