3) «102» Сумма ряда, необходимый признак сходимости

_{Сумму первых n членов числового ряда обозначают через Sn и наз. n-й частичной суммой ряда Sn=u1+u2+u3+...+un. Ряд наз-ся сходящимся, если послед-сть его частичных сумм имеет конечный предел. Если послед-сть частичных сумм не имеет конечного предела, то ряд наз-ся расходящимся. Расходящийся ряд не имеет суммы. Необх.условие сходимости ряда: если общий член un не стремится к нулю, то ряд расходится.}

Билет №6

1. «10» Миноры. Теорема о разложении. Алгебраические дополнения.

2. «68» Формула Тейлора. Разложение элементарных функций. Формула Маклорена.

3. «85» Определенный интеграл с переменным верхним пределом. Формула Ньютона — Лейбница.

4. Решить дифференциальное уравнение

1) «10» Миноры. Теорема о разложении. Алгебраические дополнения

Минором порядка k данной матрицы, где k min(m;n), называется определитель k-го порядка, полученный из матрицы А вычеркиванием (m-k) строк и (n-k) столбцов.

Пример. А= , , .

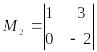Алгебраическим дополнением A_ij к элементу a_ij квадратной матрицы называется число A_ij= .

Пример. Найдем алгебраическое дополнение к элементу a₃₃.

.

Теорема 1. Определитель равен сумме попарных произведений элементов любой строки на их алгебраические дополнения.

- разложение определителя по i-й строке.

Теорема о разложении: Определитель равен сумме парных произведений элементов какого-либо ряда (строки или столбца) его на их алгебраические дополнения.

Таким образом, для определителя (3.1) справедливы следующие разложения:

разложение по i-ой строке ; разложение по j -ому столбцу

2) «68» Формула Тейлора. Разложение элементарных функций. Формула Маклорена

формула Тейлора для экспоненты такова:

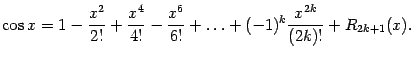
Формулой Маклорена называется формула Тейлора при а = 0:

Мы получили так называемую формулу Маклорена с остаточным членом в форме Лагранжа.Следует отметить, что при разложении функции в ряд применение формулы Маклорена предпочтительнее, чем применение непосредственно формулы Тейлора, т.к. вычисление значений производных в нуле проще, чем в какой- либо другой точке, естественно, при условии, что эти производные существуют.

3) «85» Определенный интеграл с переменным верхним пределом. Формула Ньютона — Лейбница

Символьный процессор предоставляет замечательные возможности аналитического вычисления интегралов, в том числе зависящих от параметров. Особую важность имеет вычисление интеграла с переменным пределом (верхним или нижним), для которого один из пределов интегрирования является переменной, отличной от переменной интегрирования. Нетрудно сообразить, что, с точки зрения символьного процессора, интеграл с переменным пределом является обычным определенным интегралом, зависящим от дополнительного параметра.

формула Ньютона — Лейбница даёт соотношение между двумя операциями: интегрированием и дифференцированием

Формулировка Рассмотрим интеграл от функции y = f(x) в пределах от постоянного числа a до числа x, которое будем считать переменным. Запишем интеграл в следующем виде:

Основная теорема анализа гласит, что Производная неопределенного интеграла (1) по его верхнему пределу х равна значению функции f(u) в точке u=x: F’(x)=f(x)

Другими словами, процесс интегрирования, ведущий от функции f(x) к функции F(x), «уничтожается» обратным ему процессом дифференцирования, применяемым к функции F(x).

Эта же теорема может быть сформулирована и иным образом: Функция F(x), являющаяся интегралом от функции f(x) при постоянном нижнем и переменном верхнем пределе х, есть одна из первообразных функций от функции f(x)

Здесь под первообразными функциями от функции f(x) понимаются такие функции G(x), для которых G'(x) = f(x).

Билет №7

1. «30» Точка пересечения двух прямых.

«31»Угол между двумя прямыми; условие параллельности и перпендикулярности двух прямых.

2. «63» Дифференциал функции. Геометрический смысл дифференциала.

3. «128» Биномиальный закон распределения вероятностей.

4. Решить дифференциальное уравнение