2)«72» Выпуклость графика функции. Достаточное условие выпуклости графика функции.

Теорема. Ф-я выпукла вниз(вверх) на промежутке Х тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает(убывает).

Теорема.Если вторая производная дважды дифференцируемой ф-и положительна(отрицат) внутри некоторого промежутка Х, то ф-я выпукла вниз(вверх) на этом промежутке.

Определение 1. Функция y=f(x) называется выпуклой вниз на промежутке Х, если для любых двух значений х₁, х₂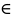 Х их этого промежутка выполняется неравенство

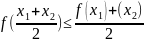
Определение 2. Функция называется выпуклой вверх на промежутке Х, если для любых двух значений х₁, х₂ Х из этого промежутка выполняется неравенство

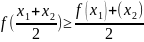
«73»Точки перегиба графика функции. Достаточное условие точек перегиба графика функции

Определение: Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх.

Из вышесказанного следует, что точки перегиба – это точки экстремума первой производной. Отсюда вытекает следующие утверждения.

Теорема (необходимое условие перегиба) Вторая производная дважды дифференцируемой функции в точке перегиба х₀ равна нулю, т.е. f’’(x)=0

Если критическая точка дифференцируемой функции не является точкой экстремума, то она есть точка перегиба.

3) «129» Локальная теорема Лапласа

Функция 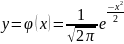называется дифференциальной функцией Лапласа.

Если вероятность p появления события А в каждом испытании постоянна и отлична от 0 до 1, то вероятность P_n(K) того, что событие А появится в n независимых испытаниях ровно k раз, приближенно значению функции: 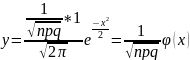, где

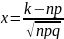
«130». Интегральная теорема Лапласа

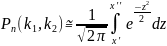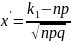Если вероятность p появления события А в каждом испытании постоянна и отлична от 0 до 1, то вероятность P_n(K1,К2) того, что событие А появится в n независимых испытаниях ровно k₁ до k₂ раз, приближенно равна значению определенного интеграла , где и

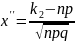
Значения функции Лапласа 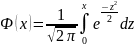приведены в таблице(учесть нечетность функции)

Тогда искомая вероятность может быть найдена по формуле:

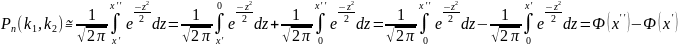
Итак, 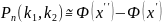, где и

Билет №10

1. «24» Декартовы прямоугольные координаты на плоскости.

«25»Полярные координаты. Связь между ними

2. «53» Классификация точек разрыва

3. «107» Знакопеременные ряды. Абсолютная и условная сходимость

4. Задача теория вероятностей

1) «24» Декартовы прямоугольные координаты на плоскости

Прямоугольные декартовые координатами точки М называют числа, определяемые формулами x=OM_x, y=OM_y, где ОМ_x – величина отрезка ОМ_x оси Оx ОМ_y – величина направленного отрезка ОМ_y оси Оy

Эти два числа x  и  y полностью определяют положение точки на плоскости, а именно: каждой паре чисел x и  y соответствует единственная точка М плоскости, и наоборот.

«25»Полярные координаты. Связь между ними

Полярная система координат задается точкой О, на­зываемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором того же направления, что и луч Ор.

Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием г от полюса О и углом φ, образован­ным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, п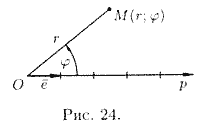 ротивоположном движению часовой стрелки) (см. рис. 24).Числа r и φ называются полярными координатами точки М, пишут М(r; φ), при этом r называют полярным радиусом, φ — полярным углом.Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком (—; ] (или 0< φ < 2r), а полярный радиус — [0;∞). В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно.