Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российская таможенная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Билеты(мат).docx

Скачиваний:

Добавлен:

26.09.2019

Размер:

523.19 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1615 16 > Следующая >>>

1.Полный дифференциал функции нескольких переменных. Производная сложной функции.

Пусть на области D задана функция двух переменных z =f(х,у), M0(x0;y0) - внутренняя точка области D, M(x0+Δx;y+Δy) - "соседняя" с M0 точка из D.

Рассмотрим полное приращение функции: ∆z=z(M)-z(M0)=z(x0+∆x,y0+∆y)-z(x0;y0)

Если Δz представлено в виде: ∆z=A∆x+B∆y+α(∆x,∆y)p

где A, B - постоянные (не зависящие от Δx, Δy), - расстояние между M и M0, α(Δx,Δy) - бесконечно малая при Δx - 0, Δy - 0; тогда функция z =f(х,у) называется дифференцируемой в точке M0, а выражение

называется полным дифференциалом функции z =f(х;у) в точке M0.

Производная сложной функции

Пусть -- область в , в которой заданы функций , . Предположим, что все значения вектор-функции

л ежат в области , в которой задана функция . Тогда можно определить композицию (или сложную функцию) :

определённую при .

2.Математическим ожиданием дискретной случайной величины.

Называется сумма вида 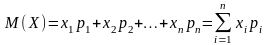где 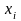- возможные значения дискретной случайной величины; 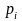- вероятность появления значения . Основные свойства: 1.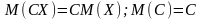 , где С – произвольная постоянная величина.

2.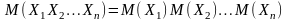 , если Х₁,Х₂,…,Х_n – взаимно независимые случайные величины.

3.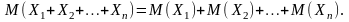 4. 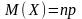, где Х – дискр. Случ.велич.; n – число испытаний с биноминальным законом распределения; p – вероятность появления события в одном испытании.

3. Диаграммы Эйлера-Венна

Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т.п.).

Операции над множествами:

Объединение множеств

Объединением АВ множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.

Символическая запись этого определения: А В={х | хА или хВ}.

Примеры объединений двух множеств:

1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А В ={2; 3; 5; 6; 7}.

2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А В=[-2/3; 2] .

Пересечение множеств

Пересечением А ? В множеств А и В называется множество, состоящее из всех элементов, принадлt; одновременно каждому из множеств А и В.

Символическая запись этого определения: А ? В={х | х А и х В}.

1) Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7} .Тогда А ? В={5; 7}.

2) Пусть А=[-1/4; 7/4], В=[-2/3; 3/2]. Тогда А ? В= [-1/4; 3/2].

Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т.е. А₁?A₂ = A₂ ?А₁и (А₁?A₂)?А₃= А₁?(A₂ ?А₃).

Разность множеств

Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.

А\В={х | х А и хВ},

На диаграмме разность А\В выделена штриховкой.

Примеры разностей множеств:

1. Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.

2. Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда А\В=(7/4;2], а В\А=[-2/3; -1/4).

Симметрическая разность С = (А\В) об. (B\А)

Билет №21

«59» Производная сложной функции. Производная обратной функции
«132» Случайная дискретная величина и ее закон распределения
«119» Решение линейного неоднородного уравнения с постоянными коэффициентами

Найти вероятность1. Производная сложной функции.

. Обычно называют внешней функцией, а - внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции.

Производная обратной функции.

2. Случайной дискретной величиной называется такая, значения которой есть конечное или счетное множество фиксированных величин. Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

Закон распределения может быть задан аналитически, в виде таблицы или графически.

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

3. Решение линейного неоднородного уравнения с постоянными коэффициентами.

Чтобы решить линейное неоднородное дифференциальное уравнение с постоянными коэффициентами y'' + py' + qy = f(x), надо решить соответствующее ему однородное уравнение y'' + py' + qy = 0, а затем найти методом неопределенных коэффициентов по виду его правой части одно частное решение.

Дифференциальное уравнение вида (1)

где , f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами. Если , то уравнение (1) называется однородным, в противном случае - неоднородным. К однородному уравнению, очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось.

Если f - непрерывная функция, то общее решение уравнения (1) состоит из суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения (1).

Чтобы решить однородное линейное уравнение с постоянными коэффициентами (1) надо составить характеристическое уравнение (2) и найти его корни . Каждому простому корню соответствует частое решение однородного уравнения (1), имеющее вид , а каждому корню кратности k - решения . Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е. , где произвольные постоянные.

Если все коэффициенты однородного уравнения (1) вещественные, то решение можно написать в вещественной форме и в случае комплексных корней . Для каждой пары комплексно сопряженных корней в формулу общего решения включаются слагаемые ,