1) «51» Бесконечно малые функции. Свойства бесконечно малых функций

Функция α(x), определенная в O (x 0), называется бесконечно малой функцией при x → x0, если limx → x0 α(x) = 0.

Свойства бесконечно малых функций:

1)Сумма фиксированного числа бесконечно малых функций при х→а тоже бесконечно малая функция при ха.

2) Произведение фиксированного числа бесконечно малых функций при ха тоже бесконечно малая функция при ха.

3)Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при ха.

4)Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

2) » Методы приближенных вычислений определенного интеграла: формула прямоугольников, формула трапеций, формула Симпсона

Суть приближенного вычисления определенных интегралов.

Так как в геометрическом смысле значение определенного интеграла есть площадь подграфика подынтегральной функции, то приближенное вычисление сводится к приближенному представлению площади подграфика в виде набора прямоугольников (в методе прямоугольников), трапеций (в методе трапеций) или ограниченных сверху параболами сегментов (в методе Симпсона).

М прямоугольников. М трапеций. М парабол (метод Симпсона).

Алгоритм действий.

1. Сначала разбиваем отрезок [a;b] интегрирования на n частей ( 2n частей для метода Симпсона или метода средних прямоугольников). Это делается по формуле для методов левых, правых прямоугольников и трапеций и по формуле *k, k=0,1,…,2n- для метода средних прямоугольников и метода Симпсона.

2. Вычисляем значения подынтегральной функции в нужных точках . f(x_k)

3. Используем соответствующую формулу.

   • Для метода левых прямоугольников .

   • Для метода средних прямоугольников .

   • Для метода правых прямоугольников .

   • Для метода трапеций

   • . Для метода парабол (Симпсона) .

3) Частные производные 1-го порядка, их геометрический смысл.

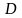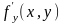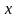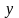Пусть функция определена в некоторой области . Если функция имеет частные производные и , то они в общем случае тоже будут функциями двух переменных и , определенных в области или ее части. Будем называть в дальнейшем функции и частными производными первого порядка (или просто первыми частными производными) функции 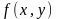. Если частные производные существуют в каждой точке области V, то они будут функциями тех же независимых переменных, что и сама функция. Геометрический смысл: Если функция имеет конечную производную в точке x0, то в окрестности U(x0) её можно приблизить линейной функцией fl(x) = f(x0) + f'(x0)(x − x0).Функция fl называется касательной к f в точке x0. Число f'(x0) является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Билет №17

1. «50» Основные свойства предела функции

2. «88» Приложения определенного интеграла (нахождение объема тела вращения, длины дуги, площади поверхности тела вращения в декартовой и полярной системах координат)

3. «109» Степенные ряды. Интервал сходимости

4. Диф. Ур