30. Оценка надёжности резервируемых восстанавливаемых систем методами теории массового обслуживания. Пример.

Система обработки данных с ненагруженным резервом может находиться в сле­дующих четырех состояниях:

1) основная и резервная система исправны;

2) основная система отказала и восстанавливается, а резервная работает;

3) резервная система отказала и восстанавливается;

4) основная и резервная системы отказали.

Разработчик системы должен оценить вероятность пребывания сис­темы в i-ом состоянии Pi(t) , а также оценить среднее время пребывания системы в исправных и неисправных состояниях с учетом процессов восстановления. Это позволит обоснованно назначить сроки профилакти­ческих мероприятий. Процессы, характеризуемые дискретными состоя­ниями во времени, могут быть представлены как марковские процессы и описаны методами теории массового обслуживания.

Поскольку состояния системы несовместны и образуют полную группу событий, то

Для вычисления вероятностей пребывания системы в i-м состоянии P_i(t) статистические характеристики процессов отказов и вос становлении - плотности вероятности переходов из i-го состояния в j-e и обратно: ,

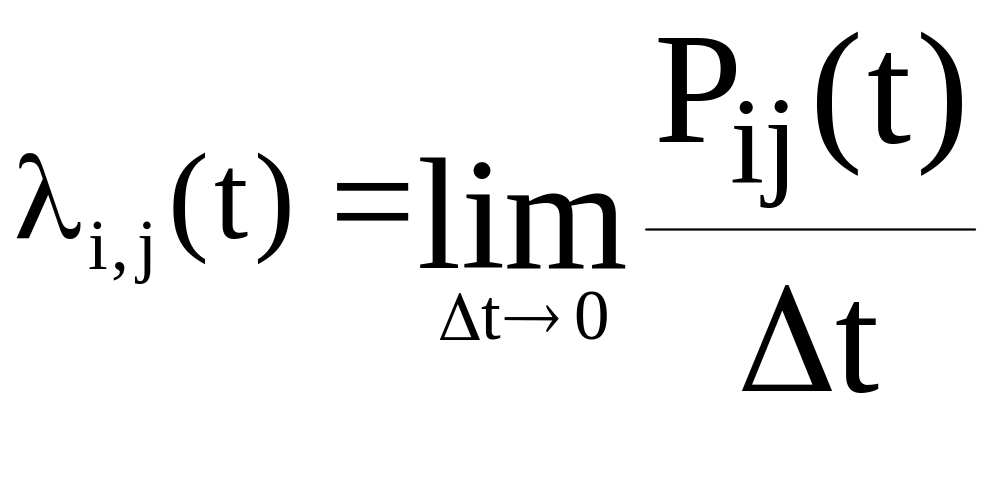Если плотности вероятностей переходов не зависят от времени, то есть λ_ij(t)=const,µ_ij(t) = const то такой процесс считается стацио­нарным. Для таких процессов можно построить граф состояний систе­мы, число вершин которого равно числу возможных состояний. Дуги графа отражают потоки отказов и восстановлений, обозначения кото­рых соответственно λ_ij и µ_ij указываются около дуг.

Размеченный граф состояний позволяет записать систему линейных дифференциальных уравнений Колмогорова. Число уравнений равно числу состояний системы, то есть числу вершин графа. Решение системы урав­нений позволяет вычислить P_i,(t), i=1,...,I. Правило составления уравнений поясняет рис. 4.1.1, на котором изображены два состояния i,j.

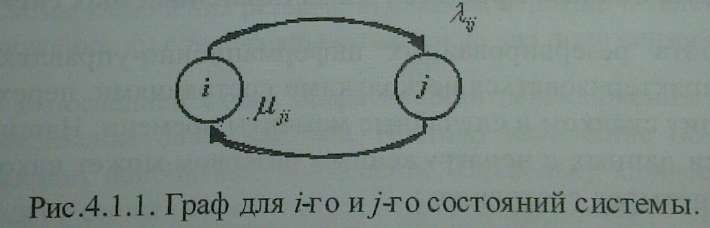
В левой части каждого уравнения записывается производная вероят­ности i-го состояния dP_i/dt. Правая часть содержит слагаемые разных зна­ков, число слагаемых равно числу дуг на графе, связанных с этим состоя­нием. Каждое слагаемое равно произведению плотности вероятности пере­хода λ_ij или µ_ij соответствующей данной дуге графа, на вероятность того состояния, из которого исходит эта дуга. Если дуга направлена из i-го со­стояния, то соответствующее произведение имеет отрицательный знак. Физически это соответствует уменьшению вероятности пребывания сис­темы в i-м состоянии. Если дуга направлена в i-е состояние, то произве­дение имеет положительный знак.

Например, для приведенного выше графа система уравнений будет такой

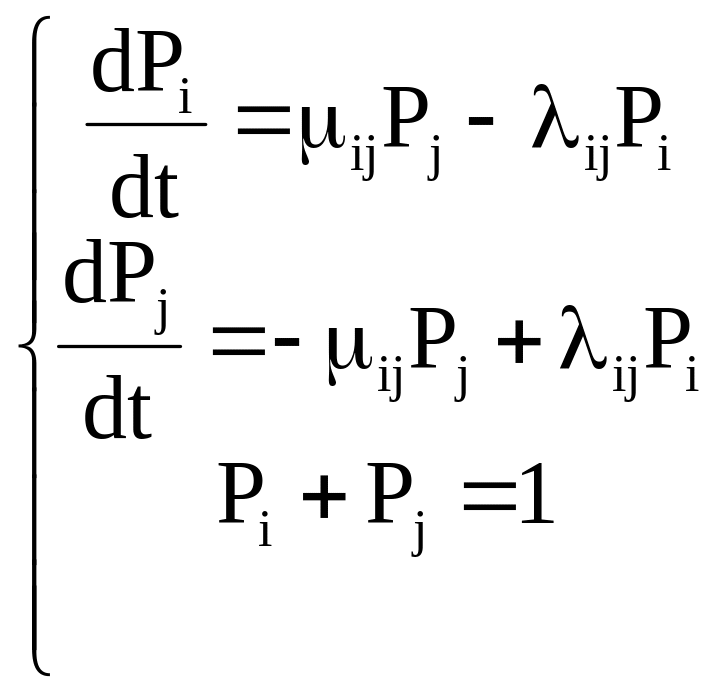
В общем виде система линейных дифференциальных уравнений, опи­сывающих непрерывный во времени марковский процесс, записывается гак:

, где

Опыт эксплуатации восстанавливаемых систем показывает, что под действием потоков отказов и восстановлений наступает установившийся режим, когда вероятности состояний системы Ц становятся практически постоянными и dpi /dt=0. Это позволяет облегчить расчеты, приравнивая нулю правые части уравнений Колмогорова и оперируя с алгебраическими уравнениям и с учетом полной группы событий.

Записанные дифференциальные уравнения состояний системы по­зволяют вычислить и средние времена ее пребывания в каждом т состоя­ний T_i , если эти уравнения представить в операторной форме. Действи­тельно, преобразование Лапласа для вероятности i-го состояния:

Сравним это выражение с выражением для средней наработки до отказа:

Из этих выражений находим, что T_i=P_i(s) при s=0. Поэтому для вычисления Ti в системе уравнений Колмогорова нужно положить ну­лю все производные dP_i/dt=0, кроме dP₁/dt, если считать, что в на­чальный момент вероятность первого состояния (исправного) Р₁(0)= 1. Тогда на основании теоремы о дифференцировании изображений в преобразовании Лапласа правая часть первого уравнения будет равна -1. В правых частях уравнений вместо Рi, подставляются Ti, и относи­тельно них решается система алгебраических уравнений.

Расчет характеристик надежности систем с использованием графа переходов особенно удобен в случаях, когда имеют место процессы отка­зов и восстановлений.