20. Абсолютная и относительная погрешности деления.

Погрешность частного: относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя.

Пример. Найти частное u = 25.7 / 3.6, если все написанные знаки делимого и делителя верны.

Решение. u = 25.7 / 3.6 = 7.14 . du = dx1 + dx2 = 0.05/25.7 + 0.05/3.6 = 0.002 + 0.014 = 0.016 . Так как u = 7.14, то Du = 0.016 · 7.14 = 0.11 . Поэтому u = 7.14 ± 0.11 .

21. Абсолютная и относительная погрешности деления.

Для частного двух чисел вычисления будут аналогичными.

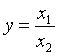
Находим натуральный логарифм и его частные производные

,

, 

следовательно, предельная относительная погрешность частного равна сумме предельных относительных погрешностей делимого и делителя.

Абсолютная погрешность результата вычисления функции нескольких приближенных чисел равна сумме произведений модуля частной производной функции на абсолютную погрешность приближенного числа.

24. Методы центральных прямоугольников, трапеций и Симпсона вычисления определенных интегралов: расчетные формулы, порядок точности, оценка погрешности, вычисление погрешности по правилу Рунге.

Требуется найти

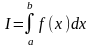
с той или иной степенью точности. Известны три классических способа сделать это.

Способ № 1: метод прямоугольников. Отрезок 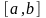разбивается на 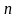равных частей: длиной 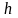, где

.

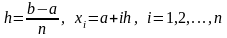Затем на каждом участке функция 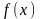заменяется на константу 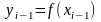, после чего искомый интеграл заменяется на интеграл от новой ступенчатой функции, т.е. на число

.

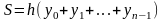Можно доказать, что справедлива следующая оценка:

,

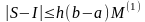где - максимум модуля первой производной функции на отрезке .

Способ № 2: метод трапеций.

В этом методе искомый интеграл после разбиения отрезка на равные части заменяется на следующую сумму (суммируются площади трапеций, а не прямоугольников, как в предыду-щем случае):

,

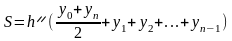где Можно доказать, что если 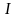- исходный обсуждаемый интеграл,то

,

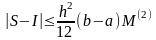где 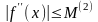на отрезке .

: Способ № 3: метод парабол(Cимпсона). В этой ситуации отрезок разбивается на 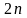равных частей: 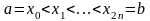, где . На участках 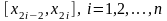, функцию заменяют на параболу, проходящую через точки и интегралом от этой параболы на участке заменяют интеграл от функции на этом же участке, после чего все эти интегралы суммируют и результаты принимают за интеграл от по всему отрезку . Полученная приближенная формула называется формулой парабол или формулой Симпсона. Вот ее окончательный

вид:

.

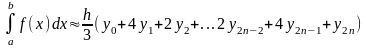Если левую часть этого приближенного равенства обозначить через I а правую – через S, то окажется выполненной следующая формула для оценки погрешности:

,

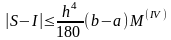где 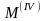- максимум на интервале четвертой производной функции .

существует еще один широко применяемый метод - метод Рунге-Кутта, который, как правило, быстрее приводит к числу , чем метод Эйлера. Сформулируем действия по методу Рунге-Кутта:

1й шаг. Фиксируем точность, с которой нужно найти значение . Обозначим это число через 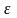. Поясним, что это означает, что числа, отличающиеся меньше, чем на , считаются одинаковыми.

2й шаг. Фиксируем произвольное 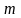и разделим отрезок 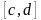на равных частей: , где .

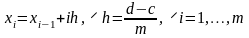3й шаг. Построим последовательность чисел

, где

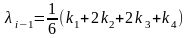и

в которой, напомним, 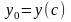. Обозначим через .

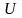4й шаг. Заменим на 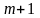и повторим шаги 2 и 3. Полученное число (т.е. послед-нее из вычисляемых на шаге 3) обозначим теперь через .

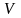5й шаг. Если окажется, что числа и отличаются друг от друга меньше, чем на , то число считается найденным и равным . В противном случае переобозначим через и вернемся к шагу 4.

Можно доказать, что когда функция из (7.4.1) имеет непрерывные частные производные, описанный процесс обязательно конечен и ответ находится действительно с любой наперед заданной точностью.