15. Абсолютная и относительная погрешности сложения.

При сложении или вычитании чисел их абсолютные погрешности складываются. Относительная погрешность суммы заключена между наибольшим и наименьшим значениями относительных погрешностей слагаемых; на практике принимается наибольшее значение.

D(a ± b) = Da + Db .

При умножении или делении чисел друг на друга их относительные погрешности складываются.

При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени.

Погрешность суммы: на практике при сложении приближенных чисел поступают следующим образом:

- выделяют числа, десятичная запись которых обрывается ранее других и оставляют их без изменения;

- остальные числа округляют по образцу выделенных, сохраняя один или два запасных десятичных знака;

- производят сложение данных чисел, учитывая все сохраненные знаки;

- полученный результат округляют на один знак.

14. Метод Ньютона–Рафсона решения систем нелинейных уравнений: алгоритм решения, условие окончания.

(1.16)

2. Алгоритм решения:

1) ввод исходных данных:

ε – допустимая абсолютная погрешность в вычислении решения;

n – количество уравнений для вычисления неизвестных x_j;

m – максимальное количество итераций;

X₀ – вектор начальных приближений

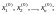
h – приращение x_j для вычисления частных производных в разностной форме;

2) вычисление элементов вектора F в начальной (текущей) точке, определяемой вектором X₀;

3) вычисление элементов матрицы J – частных производных:

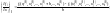
4) решение линейной системы (1.16) – вычисление элементов вектора D_x;

5) корректировка начального (текущего) приближения решения – вычисление вектора

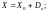
6) проверка погрешности решения по условию

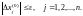
При выполнении этого условия вектор X выводится в качестве решения системы, а иначе переформируется вектор начальных приближений (X₀ = X) и осуществляется переход к пункту 2 на выполнение очередной итерации. Количество итераций ограничивается числом m. При его превышении выдается сообщение о необходимости выбора лучшего начального приближения.

16. Метод Лагранжа интерполяции данных: тип метода, вид и степень общего полинома Лагранжа, условие интерполяции, задача построения полинома Лагранжа, недостаток метода.

Метод Лагранжа

Если некоторая функция задана в (n + 1) точках x₀, x₁, … x_n, то для точного отображения ее нужно построить полином n-ой сте-пени P_n(x).

Условие интерполяции имеет вид:

P_n(x_i) = y_i, i = 0, 1, …, n, (2.1)

где x_i, y_i – значения аргумента и самой функции в узлах интерпо-ляции.

Лагранж предложил строить общий интерполяционный полином в виде суммы полиномов

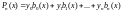, (2.2)

где y₀, y₁, … y_n – табличные значения функций;

b₀(x), b₁(x), …, b_n(x), – частные полиномы, каждый степени n.

Вид полиномов b_j, j = 0, 1, …, n:

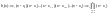. (2.3)

Примечание. В выражении (2.3) в правой части отсутствует сомножи-тель (x – x_i). Всего имеем n сомножителей-двучленов, т.е. каждый сомножи-тель первой степени, поэтому порядок полинома b_j(x) равен n.

Распишем выражения полиномов b_j(x):

• при j = 0: b₀(x) = c₀(x – x₁) (x – x₂) … (x – x_n),

здесь нет сомножителя (x – x₀), поэтому при любом

x = x_i, i = 1, 2, …, n, будет b₀(x_i) = 0

и только при x = x₀ будет b₀(x₀) ≠ 0;

• при j = 1: b₁(x) = c₁(x – x₀) (x – x₂) … (x – x_n),

здесь нет сомножителя (x – x₁), поэтому

b₁(x₀) = 0, b₁(x₂) = 0,…, b₁(x_n) = 0, но b₁(x₁) ≠ 0;

• при j = n: b_n(x) = c_n(x – x₀) (x – x₁) … (x – x_n-1),

здесь нет сомножителя (x – x_n), поэтому

b_n(x₀) = 0, b_n(x₁) = 0,…, b_n(x_n-1) = 0, но b_n(x_n) ≠ 0.

Величины x₀, x₁, … x_n, – табличные значения x_i, а величины c_j, j = 0, 1, …, n – некоторые неизвестные константы, которые надо вы-числить.

Для вычисления (n + 1)-й константы c₀, c₁, … c_n можно запи-сать на базе равенства (2.1) с учетом выражения (2.2) для полинома P_n(x) и выражения (2.3) для полиномов b_j(x) следующую систему из (n + 1)-го уравнения:

• при i = 0: x = x₀, y_i = y₀,

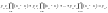
нет (x₀ – x₀) есть (x₀ – x₀) есть (x₀ – x₀)

при x = x₀ в левой части этого уравнения остается только первое сла-гаемое

;

• при i = 1: x = x₁, y_i = y₁,

есть (x₁ – x₁) нет (x₁ – x₁) есть (x₁ – x₁)

при x = x₁ в левой части этого уравнения остается только второе сла-гаемое

;

• при i = n: x = x_n, y_i = y_n,

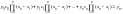
есть (x_n – x_n) есть (x_n – x_n) нет (x_n – x_n)

при x = x_n в левой части этого уравнения остается только последнее слагаемое

_.

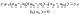Итак, получили систему

(2.4)

Отсюда следует

В общем виде можем записать

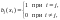(2.5)

т.е. любой полином b_j(x) = 0 при каждом x_i кроме x_j.

Из выражения (2.3) для полинома b_j(x) получаем выражение для константы c_j:

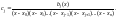(2.6)

При x = x_j имеем b_j(x_j) = 1, тогда

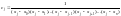. (2.7)

В выражении (2.7) x_j, j = 0, 1, …, n, и x₀, x₁, … x_n – табличные значения x, т.е. имеем все известные значения и можем вычислить значения констант c_j.

Подставив выражение (2.7) в выражение (2.3), получаем выра-жение для полинома b_j(x) в развернутой форме:

.

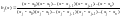Введём обозначение:

,

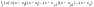тогда получим компактную запись

(2.8)

Отметим, что

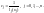
С учетом (2.8) интерполяционный полином Лагранжа можно записать в следующем виде:

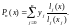(2.9)

Подставляя в (2.9) любое значение x, можно вычислить соответ-ствующее значение полинома.

Метод Лагранжа позволяет интерполировать данные на каждом отрезке между заданными точками полиномом высокой n-ой степени, всего на единицу меньшей количеством точек (интерполяционный полином един на всем интервале интерполяции). В этом состоит пре-имущество метода Лагранжа перед рассматриваемым ниже методом сплайнов.

Однако метод Лагранжа имеет недостаток: при существенном отличии («разбросе») по значению ординат y соседних точек (чередо-вание больших и малых значений) вычисляемые по выражению поли-нома значения функции в промежуточных точках между узлами интерполяции противоестественно отличаются от значений величин, характеризующих реальный процесс.

Для адекватного отображения реального колебательного проце-сса необходимо иметь промежуточные данные между амплитудными значениями.