52. Дисперсия совокупности среднеарифметических величин. Доверительные интервалы. Правило «трех сигм».

Для уменьшения влияния случайных ошибок необходимо произвести измерение данной величины несколько раз. Предположим, что мы измеряем некоторую величину x. В результате проведенных измерений мы получили значений величины :

x₁, x₂, x₃, ... x_n.      (2)

Этот ряд значений величины x получил название выборки. Имея такую выборку, мы можем дать оценку результата измерений. Величину, которая будет являться такой оценкой, мы обозначим  . Но так как это значение оценки результатов измерений не будет представлять собой истинного значения измеряемой величины, необходимо оценить его ошибку. Предположим, что мы сумеем определить оценку ошибки Δx . В таком случае мы можем записать результат измерений в виде

µ =   ± Δx        (3)

Так как оценочные значения результата измерений   и ошибки Δx не являются точными, запись (3) результата измерений должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью (3). Сам этот интервал называется доверительным интервалом.

Например, измеряя длину некоторого отрезка, окончательный результат мы записали в виде

l = (8.34 ± 0.02) мм,    (P = 0.95)

Это означает, что из 100 шансов – 95 за то, что истинное значение длины отрезка заключается в интервале от 8.32 до 8.36 мм .

Таким образом, задача заключается в том, чтобы, имея выборку (2), найти оценку результата измерений  , его ошибку Δx и надежность P.

Эта задача может быть решена с помощью теории вероятностей и математической статистики.

абсолютной погрешности x результата серии измерений, которая будет распределена по закону Гаусса:

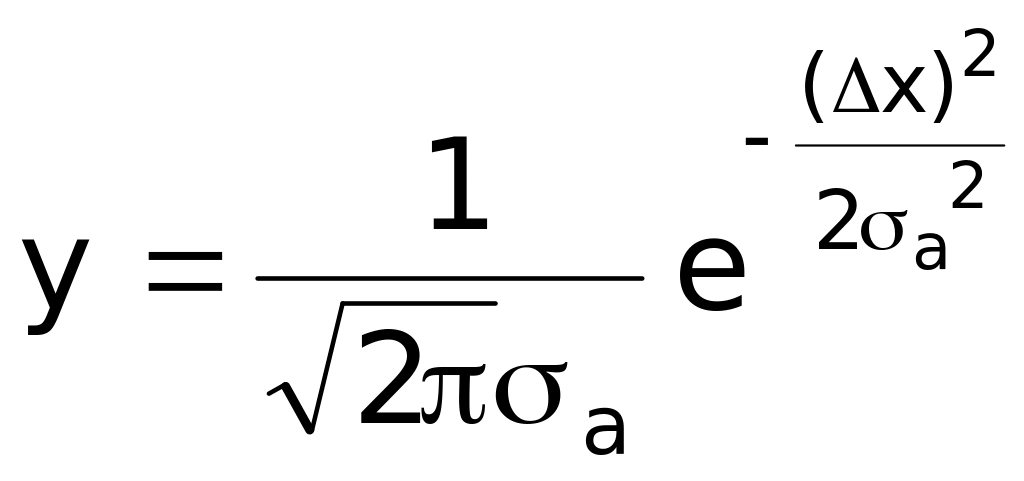из трех измерений а₁, а₂, а₃

Тогда вместо выражения Х = а  х можно записать а  х  Х  а + .

Интервал (а  х; а + х), в который по определению попадает истинное значение X называют доверительным интервалом. Надежностью уровнем значимости результата серии измерений называется вероятность  того, что истинное значение X измеряемой величины попадет в доверительный интервал. Вероятность  выражается в долях единицы или процентах. Графически надежность отражается площадью под кривой нормального распределения в пределах доверительного интервала, отнесенной к общей площади. Выбор надежности определяется характером производимых измерений. Например, к деталям самолета предъявляются более жесткие требования, чем к лодочному мотору, а к последнему значительно больше, чем к ручной тачке. При обычных измерениях ограничиваются доверительной вероятностью 0,90 или 0,95. Для любой величины доверительного интервала выраженного в долях   по формуле Гаусса может быть просчитана соответствующая доверительная вероятность. Эти вычисления проделаны и сведены в таблицу, имеющуюся практически во всей литературе по теории вероятности.

Правило сложения дисперсий.

В общем случае вариация результативного признака обусловлена различными факторами в их совокупности, а не только воздействием одного из них. Если статистическую совокупностьразбить на группы по какому-либо признаку, то наряду с изучением вариации результативного признака по всей совокупности в целом под воздействием всех факторов получаем возможность изучить вариацию для каждой из составляющих всю совокупность групп по отдельности. Также можно изучить при этом вариацию между группами. В простейшем случае вся исходная совокупность разбивается на отдельные группы по одному фактору. Тогда указанный выше анализ вариации сводится к расчету и анализу трех видов дисперсии: общей, внутригрупповой и межгрупповой. Общая дисперсия измеряет вариацию результативного признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

Межгрупповая дисперси δ² характеризует систематическую вариацию под воздействием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних от общей средней для всей совокупности:

, (7.6)

где f — численность единиц в группе (частота).

Внутригрупповая дисперсия есть уже известная нам дисперсия (для всей совокупности, называемая общей), но теперь эта формула применяется только к отдельной группе. Соответственно и обозначается она σ² , но уже с индексом i, который подчеркивает, что расчет выполняется для отдельной i-группы.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. ту ее часть, которая обусловлена влиянием прочих (неучтенных) факторов, отличных от основания группировки. По отдельным внутригрупповым дисперсиям, рассматривая их как значения некоторого особого признака, рассчитывают среднюю по внутригрупповым дисперсиям, которая уже характеризует вариацию по всей совокупности в целом под воздействием всех прочих (неучтенных) факторов, отличных от основания группировки.

Существует простая и важная формула, связывающая общую дисперсию, межгрупповую дисперсию и среднюю по внутригрупповым дисперсиям:

. (7.7)

Это означает, что общая дисперсия равна сумме межгрупповой дисперсии и средней по внутригрупповым дисперсиям. Следовательно, зная две из трех дисперсий, можно всегда найти и третью.

Правило сложения дисперсий показывает, что чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый результативный признак. Такие соображения естественным образом приводят к количественной характеристике такого влияния, мере стохастической связи между признаками. Она называется эмпирическим коэффициентом детерминации и обозначается η² , характеризуя силу влияния группировочного признака на образование общей вариации:

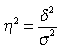. (7.8)

При отсутствии связи он просто равен нулю, при чисто функциональной связи — 1. В общем случае коэффициент детерминации принимает значения между 0 и 1. Это видно и из правила сложения дисперсий.

Помимо коэффициента детерминации используют также и эмпирическое корреляционное отношение, которое представляет собой корень квадратный из коэффициента детерминации. И опять оно весьма подходит для измерения линейной связи.

В общем случае нелинейной связи предпочтительнее использовать, что правильнее, коэффициент детерминации. Если связь отсутствует, то корреляционное отношение равно нулю и, следовательно, все групповые средние равны между собой, а межгрупповой вариации просто в этом случае нет.

Группировочный признак при этом никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение равно 1. Дисперсия групповых средних равна общей дисперсии и межгрупповой дисперсии, поэтому внутригрупповой вариации не будет. Таким образом, группировочный признак целиком определяет вариацию изучаемого результативного признака.

Правило трёх сигм

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклоненипрактически равна нулю.Это правило называется правилом трех сигм. На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

53.Дельта-функция Дирака. Пример расчета распределения электростатического потенциала (не найдено).

(Δ-функция Дирака), символ, применяемый в математической физике при решении задач, в которые входят сосредоточенные величины (нагрузка, заряд и т. п.). Дельта-функция — простейшая обобщённая функция; она характеризует, например, плотность распределения масс, при котором в одной точке сосредоточена единичная масса, а любой интервал, не содержащий этой точки, свободен от масс.

П. Дирак в книге «Принципы квантовой механики» [5] определил дельта-функцию δ(x) следующим образом:

.

Кроме того задается условие:

Наглядно можно представить график функции, похожей на δ(x), как показано на рисунке 1.

Ч ем более у зкой сделать полоску между левой и правой ветвью, тем выше должна быть эта полоска, для того чтобы площадь полоски (т.е. интеграл) сохраняла свое заданное значение, равное 1. При сужении полоски мы приближаемся к выполнению условия δ(x) = 0 при x ≠ 0, функция приближается к дельта-функции.

Такое представление общепринято в физике.

Следует подчеркнуть, что δ(x) не является функцией в обычном смысле, так как из этого определения следуют несовместимые условия с точки зрения классического определения функции и интеграла:

при и .

В классическом анализе не существует функции, обладающей свойствами, предписанными Дираком.

Обобщенной функцией называется всякий линейный непрерывный функционал, определенный на основном пространстве К

Числовую функцию f, определенную на некотором линейном пространстве L, называют функционалом.

Задачи, приводящие к определению дельта-функции Дирака.

С физической точки зрения, функция Дирака, применяемая в математической физике при решении задач, в которые входят сосредоточенные в одной точке величины (нагрузка, заряд и т. п.), представлена как простейшая обобщенная функция, позволяющая записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или приложенной в точке a пространства R_n. Она характеризует, например, плотность распределения масс, при котором в одной точке сосредоточена единичная масса, а любой интервал, не содержащий этой точки, свободен от масс.

Дельта-функция - функционал, сопоставляющий по формуле =φ(0) каждой непрерывной функции φ число φ(0)- ее значение в нуле.

Функция δ(x) применяется не только в механике, а во многих разделах математики, в частности при решении многих задач уравнений математической физики.

Пусть f(t)- функция, непрерывная на (a;b), а - иглообразная функция. Для дальнейшего введения определения дельта-функции Дирака рассмотрим поведение интеграла при

при a<0<b

(7)

Если же числа a и b одинаковых знаков (a<b<0 или 0<a<b), то есть (a;b) не содержит внутри себя точки t=0, то

при всех достаточно малых λ.

Если числа a и b имеют одинаковые знаки, то при , если a>0 (рис.6), или при , если b<0 (рис.7), интервал не будет пересекаться с (a;b ), а поэтому для всех

и .

Следовательно,

(8)

Введём обозначение:

(9)

Таким образом, δ(t) – обобщенная функция, характеризующая предельное поведение иглообразной функции при и использующаяся при вычислении интегралов.

Дельта-функцию можно применять и формально, пользуясь лишь следующим ее основным свойством, вытекающим из равенств (7) - (9) для любой непрерывной функции.

(10)

Введем подстановку = , то

(11)

Свойство, описываемое соотношениями (10) и (11) называют фильтрующим свойством дельта-функции.

54. Интерполяционный полином Ньютона.

Постановка задачи

Пусть задана функция  .  Пусть заданы точки   из некоторой области  . Пусть значения функции   известны только в этих точках. Точки   называют узлами интерполяции.  - шаг интерполяционной сетки. Задача интерполяции состоит в поиске такой функции   из заданного класса функций, что 

Метод решения задачи

Полином Лагранжа

Представим интерполяционную функцию в виде полинома где   - полиномы степели n вида: Очевидно, что   принимает значение 1 в точке   и 0 в остальных узлах интерполяции. Следовательно в точке   исходный полином принимает значение  Таким образом, построенный полином   является интерполяционным полиномом для функции   на сетке  . 

Полином Ньютона

Интерполяционный полином в форме Лагранжа не удобен для вычислений тем, что при увеличении числа узлов интерполяции приходится перестраивать весь полином заново. Перепишем полином Лагранжа в другом виде: где   - полиномы Лагранжа степени i ≤ n. Пусть    . Этот полином имеет степень i и обращается в нуль при  .  Поэтому он представим в виде: , где   - коэффициент при  . Так как   не входит в  , то   совпадает с коэффициентом при   в полиноме  . Таким образом из определения   получаем: где  Препишем формулу   в виде  Рекуррентно выражая   пролучам окончательную формулу для полинома:  Такое представление полинома удобно для вычисления, потому что увеличение числа узлов на единицу требует добавления только одного слагаемого.