1.7. Метрические характеристики графов

Рассмотрим связный граф . Длина какого-либо маршрута в графе – это число ребер в нем. Обозначим через длину кратчайшей цепи между вершинами и . Она называется расстоянием между вершинами и . Введем другие величины в графе, связанные с метрикой.

• Если , то матрица , где , называется матрицей расстояний. Матрица симметрична.

• Для фиксированной вершины величина называется эксцентриситетом вершины . Эксцентриситет вершины равен расстоянию от данной вершины до наиболее удаленной от нее. Если – матрица расстояний, то эксцентриситет равен наибольшему из чисел в -ой строке.

• Максимальный среди эксцентриситетов вершин называется диаметром графа,

• Вершина называется периферийной, если .

• Минимальный из эксцентриситетов вершин называется радиусом графа, .

• Вершина называется центральной, если .

• Множество центральных вершин называется центром графа.

Пример 1.7.1. Найдем метрические характеристики графа , изображенного на рис. 1.7.1. Матрица расстояний этого графа имеет вид:

Эксцентриситеты вершин равны: следовательно, Вершины 1 и 3 являются периферийными. Минимальный из эксцентриситетов вершин графа равен 2, следовательно, радиус графа Так как , то вершины – центральные и образуют центр графа.

Нахождение центральных вершин имеет практическое значение. Пусть, например, граф представляет собой сеть дорог, то есть вершины соответствуют населенным пунктам, а ребра – дорогам между ними. Требуется оптимально разместить пункты обслуживания. В подобных задачах оптимизация заключается в минимизации расстояния от места обслуживания до наиболее удаленного населенного пункта. Следовательно, местами размещения должны быть центральные вершины графа. В реальных задачах приходится учитывать и другие обстоятельства: расстояния между населенными пунктами, стоимость проезда, время проезда и т.д. Для учета этих параметров используются взвешенные графы.

1.8. Представления графов

В большинстве случаев граф в памяти компьютера задается матрицей. Существуют различные виды матриц, ассоциированные с графами. Выбор наилучшего представления определяется требованиями конкретной задачи. Ниже приведены несколько наиболее часто используемых представлений с указанием динамической меры сложности алгоритма – объема памяти для каждого представления (см. раздел 2). Здесь – число вершин, – число ребер графа. Эти представления пригодны и для ориентированных графов, а также после некоторой модификации и для псевдографов. Представления иллюстрируются на примерах графа и орграфа , диаграммы которых представлены на рис. 1.8.1 и 1.8.2.

1. Матрица смежности вершин графа: матрица с элементами

Для мультиграфа (число ребер, соединяющих вершины и ).

Пример 1.8.1. Матрицы смежности вершин графа и орграфа имеют вид:

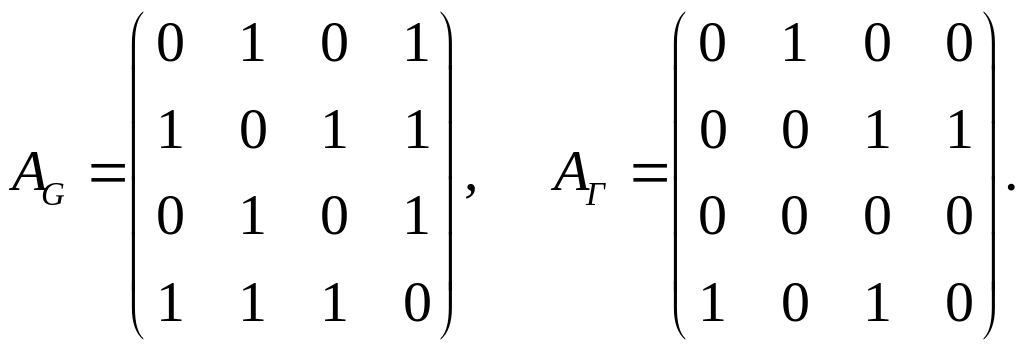
Для матрицы смежности

Теорема 1.8.1. Два графа изоморфны тогда и только тогда, когда их матрицы смежности вершин получаются друг из друга одновременными перестановками строк и столбцов (т.е. одновременно с перестановкой i-ой и j-ой строк переставляются в i-ый и j-ый столбцы).

Доказательство. Пусть два графа и порядка изоморфны. Тогда существует биекция , заданная на множестве вершин графа и сохраняющая смежность вершин. Если – матрица смежности графа , а – матрица смежности графа , то, очевидно, в силу изоморфизма,

Следовательно, из матрицы матрица получается перестановкой строк и столбцов согласно соответствию

В силу симметричности отношения изоморфизма, аналогично из матрицы

может быть получена матрица . Обратно, если в результате динаковой перестановки строк и столбцов из матрицы получается матрица, равная матрице , то указана биекция, сохраняющая смежность, т.е. изоморфизм графов и .

Пример 1.8.2. Матрицы смежности вершин первого и второго графов, изображенных на рис. 1.2.2, имеют вид:

Матрица получается из матрицы одновременной перестановкой второй и третьей, а затем третьей и пятой строк и столбцов. Следовательно, эти графы изоморфны.

2. Матрица инцидентности графа: матрица с элементами

строки которой соответствуют вершинам, а столбцы – ребрам.

Для ориентированного графа

Пример 1.8.3. Матрицы инцидентности графа и орграфа имеют вид:

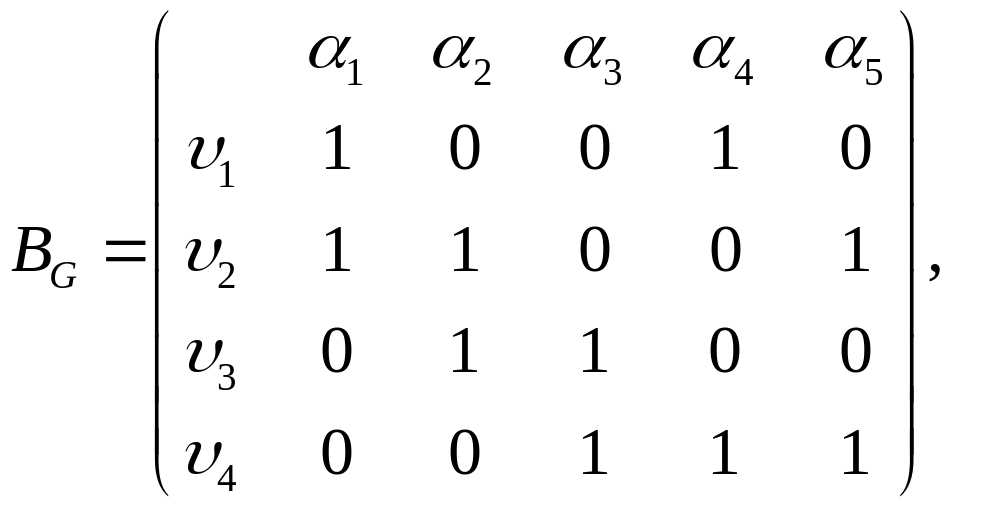
Динамическая мера сложности алгоритма для матрицы инцидентности

Аналогично теореме 1.8.1 справедлива следующая теорема.

Теорема 1.8.2. Два графа (орграфа) изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга некоторыми перестановками строк и столбцов.

Пример 1.8.4. Матрицы инцидентности графа , изображенного на

рис. 1.8.3, и графа (рис. 1.8.4) имеют вид:

.

Матрица получается из матрицы перестановкой 3-го и 5-го, а затем 5-го и 6-го столбцов. Следовательно, эти графы изоморфны.

3. Списки смежности вершин графа (орграфа). Ориентированный или неориентированный граф может быть однозначно представлен списком смежности своих вершин. Для каждой вершины ее список смежности (adjacency – смежность) состоит из вершин, смежных с ней. Списки смежности составляются для каждой вершины.

Для неориентированного графа , для орграфа .

Пример 1.8.5. Списки смежности вершин графа и орграфа , изображенных на рис. 1.8.1 и рис. 1.8.2, имеют вид:

4. Массивы ребер (дуг). При описании графа списком его ребер каждое ребро представляется парой инцидентных ему вершин. Это представление реализовывается двумя массивами: , где – число ребер. Каждый элемент в массиве является меткой вершины, а i-ое ребро выходит из вершины и входит в вершину .

Пример 1.8.6. Массивы ребер графа и массивы дуг орграфа , изображенные на рис. 1.8.1. и рис. 1.8.2, имеют соответственно вид:

.

Для массива ребер (дуг) .

5. Матрица весов графа: матрица с элементами , где – вес ребра (дуги), соединяющего вершину с вершиной . Веса несуществующих ребер (дуг) полагают равными или в зависимости от приложений. Матрица весов графа является обобщением матрицы смежности.

Отметим, что каждое представление определяет граф с точностью до изоморфизма, а выбор представления графа во многих задачах является решающим для эффективности алгоритма.