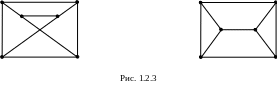1.2. Морфизмы графов

Пусть и – графы. Отображение (функция) называется гомоморфизмом, если для любых вершин из условия следует

Два графа и называются изоморфными (обозначается ), если существует биекция , сохраняющая смежность вершин:

Изоморфизм графа на себя называется автоморфизмом.

Пример 1.2.1. Рассмотрим граф рис. 1.2.1(a), состоящий из множества вершин и множества дуг и ребер (смешанный граф) . Граф (рис. 1.2.1(б)) является гомеоморфным образом графа при гомоморфизме , в котором . Граф , изображенный на рис. 1.2.1(в), изоморфен графу . Изоморфизм задается так: . Отображение , при котором , , является автоморфизмом графа .

Пример 1.2.2. Следующие три внешне различные диаграммы на рис. 1.2.2 являются диаграммами одного и того же графа .

Изоморфизм задается следующим образом: .

Рис. 1.2.1

Числовые характеристики графа, одинаковые для всех изоморфных графов, называются инвариантами графа. Например, число вершин и ребер (дуг) является инвариантами графа. Пока не известно ни одной нетривиальной полной системы инвариантов, определяющей граф с точностью до изоморфизма. Так, число ребер и число смежных вершин для каждой вершины не определяют граф. На рис. 1.2.3 изображены графы, у которых эти инварианты совпадают, но графы при этом не изоморфны.

Отношение изоморфизма графов является отношением эквивалентности. Следовательно, множество всех графов разбивается на классы эквивалентности, так что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны. Изоморфные графы естественно отождествлять и их можно изображать одинаковым рисунком.

В некоторых ситуациях все же приходится различать изоморфные графы,

и тогда полезно понятие «помеченный граф». Граф порядка называется помеченным, если его вершинам присвоены некоторые метки, например номера . Отождествив каждую из вершин графа с ее номером (и, следовательно, множество вершин – с множеством чисел ), определим равенство помеченных графов и одного и того же порядка: тогда, когда

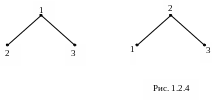
. На рис. 1.2.4 изображены три разных помеченных графа.

1.3. Степени вершин

Число ребер, инцидентных вершине , называется степенью вершины и обозначается или . Последовательность степеней вершин графа называется степенной последовательностью. На рис. 1.3.1 приведена диаграмма графа , степень каждой вершины которого равна трем.

Если степень вершины равна нулю, то такая вершина графа называется изолированной. Если степень вершины равна единице, то вершина графа называется висячей. Для графа, изображенного на рис. 1.3.2: , вершина 5 – висячая, вершина 4 – изолированная.

Для ориентированного графа число дуг, исходящих из вершины , называется полустепенью исхода и обозначается через , а число дуг, входящих в вершину , – полустепенью захода и обозначается .

Теорема 1.3.1. [Эйлер Л.]. Пусть – мультиграф с вершинами и ребрами, – степень i-й вершины , тогда сумма степеней вершин графа равна удвоенному количеству ребер.

Доказательство. Пересчитаем число ребер в каждой вершине и сложим эти числа. Тогда каждое ребро будет подсчитано два раза. Поэтому общее число ребер мультиграфа равно половине этой суммы .

Этот результат, известный еще более двухсот лет назад Эйлеру, часто называют леммой о рукопожатиях. Из нее следует, что если несколько человек обменялись рукопожатиями, то общее число рукопожатий обязательно четно, так как в каждом рукопожатии участвуют две руки (при этом каждая рука считается столько раз, сколько она участвует в рукопожатиях).

Следствие 1.3.1. В каждом мультиграфе число вершин нечетной степени четно.

Действительно, пусть – вершины с нечетной степенью, а – вершины с четной степенью. Тогда число

– четное. Так как то – четное число. Следовательно, число вершин нечетной степени – четно.