- •В. Н. Степанов дискретная математика: графы и алгоритмы на графах
- •Предисловие
- •1. Основные понятия теории графов
- •1.1. Граф и его разновидности
- •1.2. Морфизмы графов
- •1.3. Степени вершин
- •1.4. Маршруты, цепи, циклы, связность
- •1.5. Операции над графами
- •1.6. Примеры графов
- •1.7. Метрические характеристики графов
- •1.8. Представления графов
- •2. Алгоритмы и сложность
- •2.1. Понятие алгоритма
- •2.2. Сложность алгоритма
- •2.3. Запись алгоритма
- •3. Обходы графов
- •3.1. Поиск в глубину на графе
- •3.2. Поиск в ширину на графе
- •3.3. Алгоритм выделения компонент связности
- •4. Деревья
- •4.1. Деревья. Свойства деревьев
- •4.2. Остовы. Теорема Кирхгофа
- •4.3. Теорема Кэли
- •4.4. Фундаментальная система циклов. Цикломатическое число
- •4.5. Алгоритм отыскания фундаментального множества циклов на графе
- •5. Остов минимального веса. Алгоритм Краскала и Прима
- •5.1. Алгоритм д. Краскала
- •5.2. Алгоритм р. Прима
- •6. Кратчайшие пути между вершинами графа
- •6.1. Алгоритм Дейкстры
- •6.2. Алгоритм Флойда
- •7. Эйлеровы графы
- •7.1. Теорема Эйлера
- •7.2. Алгоритм Флёри
- •8. Гамильтоновы графы
- •8.1. Гамильтоновы маршруты. Задача коммивояжера
- •8.2. Существование гамильтоновых маршрутов
- •9. Алгоритмы отыскания гамильтоновых циклов
- •9.1. Алгоритм с возвратом (полного перебора)
1.5. Операции над графами
Рассмотрим некоторые основные операции, производимые над графами.
1.
Дополнение
графа.
Дополнением графа
называется граф
![]() ,
где
,
где
![]() и
и
![]() ,
то есть на вершинах графа
строится полный граф, а затем из этого
полного графа удаляются ребра графа
.
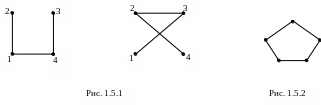
На рис. 1.5.1 граф справа является дополнением
графа слева. Графы, изображенные на рис.
1.5.1, взаимодополнительные и изоморфные.
Биекция, определяющая изоморфизм, может
быть задана в виде
,
то есть на вершинах графа
строится полный граф, а затем из этого
полного графа удаляются ребра графа
.
На рис. 1.5.1 граф справа является дополнением
графа слева. Графы, изображенные на рис.
1.5.1, взаимодополнительные и изоморфные.
Биекция, определяющая изоморфизм, может
быть задана в виде
![]()
![]()
|
|
|
Самодополнительный граф – это граф, изоморфный своему дополнению. На рис. 1.5.2 изображен еще один самодополнительный граф.
2. Объединение графов. Объединением графов и
(обозначается
![]() )
называется граф
,
множеством вершин которого является
)
называется граф
,
множеством вершин которого является
![]() ,
а множеством ребер
,
а множеством ребер
![]() (рис. 1.5.3). Объединение графов дизъюнктивное,
если объединяемые графы не имеют общих
вершин:
(рис. 1.5.3). Объединение графов дизъюнктивное,
если объединяемые графы не имеют общих
вершин:
![]() .
Дизъюнктивное объединение графов
обозначается
.
Дизъюнктивное объединение графов
обозначается
![]() .
.
|
3. Пересечение графов. Пересечением графов и
(обозначается
![]() )
называется граф
,
где
)
называется граф
,
где
![]()
![]() (рис. 1.5.4).
(рис. 1.5.4).
|
4.
Соединение графов.
Соединение графов
и
(обозначается
![]() ,
при условии
,
при условии
![]() )
состоит из
и всех ребер
)
состоит из
и всех ребер
![]() где
где
![]() и
и
![]() (рис. 1.5.5).
(рис. 1.5.5).
5.
Произведение графов.
Произведением
![]() графов
и
называется граф
графов
и
называется граф
![]() ,
в котором
,
в котором
![]()
![]()
тогда
и только тогда, когда
![]() и
и
![]() или
или
![]() и
и
![]() Пример произведения графов представлен
на рис. 1.5.6.
Пример произведения графов представлен
на рис. 1.5.6.
6.
Стягивание графа.
Пусть дан граф
и ребро
![]() соединяющее вершины
и
.
Операция удаления ребра
и отождествление вершин
и
соединяющее вершины
и
.
Операция удаления ребра
и отождествление вершин
и
![]() называется стягиванием
(рис. 1.5.7).
называется стягиванием
(рис. 1.5.7).
=
|
|
|
|
7.
Реберный граф.
Для произвольного графа
реберный граф
![]() определяется следующими двумя условиями:
определяется следующими двумя условиями:
1) вершины графа взаимно однозначно сопоставлены ребрам гра- фа .
2)
вершины
![]() и
и
![]() смежны в
тогда и только тогда, когда соответствующие
им ребра
смежны в
тогда и только тогда, когда соответствующие
им ребра
![]() и
и
![]() смежны в
.
смежны в
.
Реберный граф строится следующим образом. На каждом ребре графа выбирается фиксированная точка, например, середина этого ребра. Пара таких вершин и соединяется новым ребром, принадлежащим тогда и только тогда, когда соответствующие ребра в графе имеют общую вершину. На рис. 1.5.8 слева изображен граф , а справа – его реберный граф .