- •В. Н. Степанов дискретная математика: графы и алгоритмы на графах
- •Предисловие
- •1. Основные понятия теории графов
- •1.1. Граф и его разновидности
- •1.2. Морфизмы графов
- •1.3. Степени вершин
- •1.4. Маршруты, цепи, циклы, связность
- •1.5. Операции над графами
- •1.6. Примеры графов
- •1.7. Метрические характеристики графов
- •1.8. Представления графов
- •2. Алгоритмы и сложность
- •2.1. Понятие алгоритма
- •2.2. Сложность алгоритма
- •2.3. Запись алгоритма
- •3. Обходы графов
- •3.1. Поиск в глубину на графе
- •3.2. Поиск в ширину на графе
- •3.3. Алгоритм выделения компонент связности
- •4. Деревья
- •4.1. Деревья. Свойства деревьев
- •4.2. Остовы. Теорема Кирхгофа
- •4.3. Теорема Кэли
- •4.4. Фундаментальная система циклов. Цикломатическое число
- •4.5. Алгоритм отыскания фундаментального множества циклов на графе
- •5. Остов минимального веса. Алгоритм Краскала и Прима
- •5.1. Алгоритм д. Краскала
- •5.2. Алгоритм р. Прима
- •6. Кратчайшие пути между вершинами графа
- •6.1. Алгоритм Дейкстры
- •6.2. Алгоритм Флойда
- •7. Эйлеровы графы
- •7.1. Теорема Эйлера
- •7.2. Алгоритм Флёри
- •8. Гамильтоновы графы
- •8.1. Гамильтоновы маршруты. Задача коммивояжера
- •8.2. Существование гамильтоновых маршрутов
- •9. Алгоритмы отыскания гамильтоновых циклов
- •9.1. Алгоритм с возвратом (полного перебора)
1.4. Маршруты, цепи, циклы, связность
Маршрутом
в графе
называется чередующаяся последовательность
вершин и ребер
![]() ,
в которой любые два соседних элемента
инцидентны. Число ребер в маршруте (с
повторениями) называется длиной
маршрута.
Это определение подходит также для
псевдо-, мульти- и орграфов. Для «обычного»
графа достаточно указать только
последовательность вершин или только
последовательность ребер.
,
в которой любые два соседних элемента
инцидентны. Число ребер в маршруте (с
повторениями) называется длиной
маршрута.
Это определение подходит также для
псевдо-, мульти- и орграфов. Для «обычного»
графа достаточно указать только
последовательность вершин или только
последовательность ребер.
Маршрут называется цепью, если все его ребра различные. Цепь, соединяющая вершины
 и
,
обозначается
и
,
обозначается
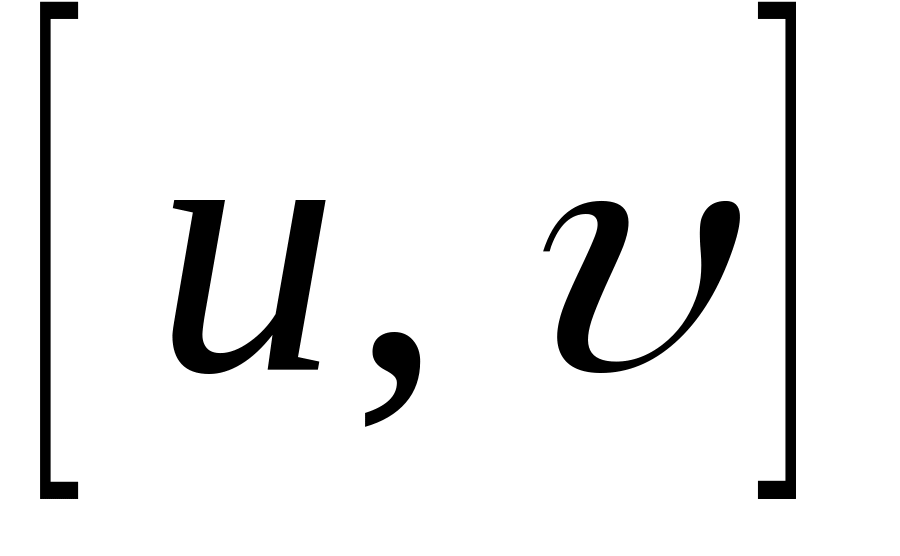 ,
и тогда вершина
называется достижимой
из вершины
,
и тогда вершина
называется достижимой
из вершины

Маршрут называется замкнутым, если
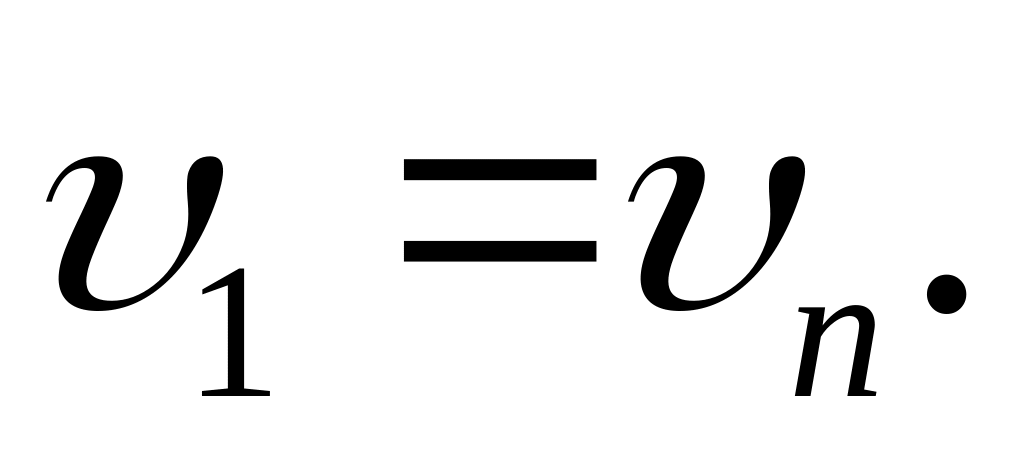
Замкнутая цепь называется циклом.
Цепь называется простой, если все вершины (а значит, и ребра) различны.
Простая замкнутая цепь называется простым циклом.
Наименьшая длина цикла в графе называется обхватом.
Граф без циклов называется ациклическим.
Для ориентированных графов цепь называется путем, а цикл – контуром.
Пример
1.4.1.
Рассмотрим граф, изображенный на рис.
1.4.1. В нем
![]() – маршрут длины 3, но не цепь;
– маршрут длины 3, но не цепь;
![]() – цепь (все ребра различные), но не
простая цепь (вершина
– цепь (все ребра различные), но не
простая цепь (вершина
![]() встречается дважды);
встречается дважды);
![]() – простая цепь;
– простая цепь;
![]() – цикл, но не простой (вершина
встречается дважды);
– цикл, но не простой (вершина
встречается дважды);
![]() – простой цикл.
– простой цикл.
Теорема 1.4.1. Пусть в графе степень каждой вершины не меньше 2. Тогда граф содержит цикл.
Доказательство.
Пусть
– произвольная вершина из
![]() Построим последовательность ребер
Построим последовательность ребер
![]() выбирая
смежной с
и отличной от
;
смежной с
и отличной от
и т.д. По условию теоремы на каждом шаге
очередная вершина существует. В силу
конечности множества вершин
в последовательности
выбирая
смежной с
и отличной от
;
смежной с
и отличной от
и т.д. По условию теоремы на каждом шаге
очередная вершина существует. В силу
конечности множества вершин
в последовательности
![]() встретится вершина
встретится вершина
![]() ,
которая встречалась раньше. Выбирая
,
которая встречалась раньше. Выбирая
![]() минимальным с этим свойством, получим
цикл.
минимальным с этим свойством, получим
цикл.
|
|
Граф называется связным, если для любых двух его вершин и существует соединяющая их простая цепь .
Отношение
связности на множестве вершин является
отношением эквивалентности. Рефлексивность
следует из того факта, что каждая вершина
связана сама с собой тривиальной цепью.
Симметричность следует из того, что,
взяв вершины цепи
в обратном порядке, получим цепь из
в
.
Транзитивность также очевидна: объединив
цепи из
в
и из
в
![]() ,
получим цепь из
в
.
Классы эквивалентности по отношению
связности называются компонентами
связности графа.
Число компонент связности графа
обозначается
,
получим цепь из
в
.
Классы эквивалентности по отношению
связности называются компонентами
связности графа.
Число компонент связности графа
обозначается
![]() .
Граф
является связным тогда и только тогда,
когда
.
Граф
является связным тогда и только тогда,
когда
![]() Если
Если
![]() ,
то
– несвязный граф. Граф, состоящий только
из изолированных вершин, называется
вполне
несвязным.
Очевидно, что всякий несвязный граф
,
то
– несвязный граф. Граф, состоящий только
из изолированных вершин, называется
вполне
несвязным.
Очевидно, что всякий несвязный граф
можно
представить в виде объединения связных
графов (компонент связности). На рис.
1.4.2 изображен граф с четырьмя компонентами
связности. Ребро графа, после удаления
которого увеличивается число компонент
связности, называется мостом.
На рис. 1.5.1 слева ребро
![]() – мост.
– мост.