6.2. Алгоритм Флойда
Алгоритм Флойда находит кратчайшие пути между всеми парами вершин в орграфе. В принципе эту задачу можно решить n-кратным применением алгоритма Дейкстры, где n – количество вершин графа. Однако существует менее трудоемкий алгоритм, разработанный Р. Флойдом в 1962 г.
В
алгоритме Флойда строится последовательность
матриц
,
,
где
– матрица весов графа
а
– длина кратчайшего пути из вершины
и
,
все промежуточные вершины которого
содержатся в множестве
,
т.е. содержатся в первых k
вершинах.
Очевидно,
что
– искомое расстояние между вершинами
и
.
Матрицы
и
связаны следующей рекуррентной формулой:
.
Действительно,
рассмотрим кратчайший
-путь
P
с промежуточными вершинами из множества
.
Возможно два случая: либо вершина
входит в этот путь, либо нет.
Если
вершина
не входит в путь P,
то, как легко видеть,
.
Если
же вершина
входит в путь P,
то, разбивая этот путь на пути от
до
и от
до
,
получаем два новых пути, все промежуточные
вершины которых входят в множество
.
Так как всякий подпуть кратчайшего пути
сам является кратчайшим путем между
соответствующими вершинами, то справедливо
доказываемое равенство.
Равенство
позволяет легко находить расстояния
между всеми парами вершин: нужно
последовательно вычислить для всех пар
вершин значения
и учесть, что расстояние от
до
равно
.
В
приводимом ниже алгоритме предполагается,
что
и
,
если дуга
отсутствует. Неотрицательность весов
дуг не предполагается, однако считается,
что в графе нет контуров отрицательной
длины. В алгоритме используется двумерный
массив Pred
размера
.
Pred
равен номеру вершины, которая является
предпоследней в кратчайшем
-пути
(последней вершиной в таком пути является
вершина
).
Если Pred
,
то, просмотрев значение Pred
,
получим следующую вершину в
-пути.
Таким образом, двигаясь по элементам
массива Pred,
легко построить путь для любой пары
вершин.
Алгоритм 6.2.1. Вычисление расстояний между всеми парами вершин.
Вход: граф G = (V,E,c), заданный матрицей весов порядка n.
Выход:
расстояния
для всех пар
,
матрица Pred,
в которой Pred
равно
номеру предпоследней вершины в кратчайшем
-пути.
1. begin
2. for i:=1 to n do
3. for j:=1 to n do
4. begin
5.
;
Pred
[i,
j]:=i;
6. end;
7. for k:=1 to n do
8. for i:=1 to n do
9. for j:=1 to n do
10.
if
then
11. begin
12.
13. Pred [i, j]:=Pred [k, j]
14. end
15. end.
Пример 6.2.1. Найти кратчайшие расстояния между всеми парами вершин в орграфе на рис. 6.2.1.
|
.
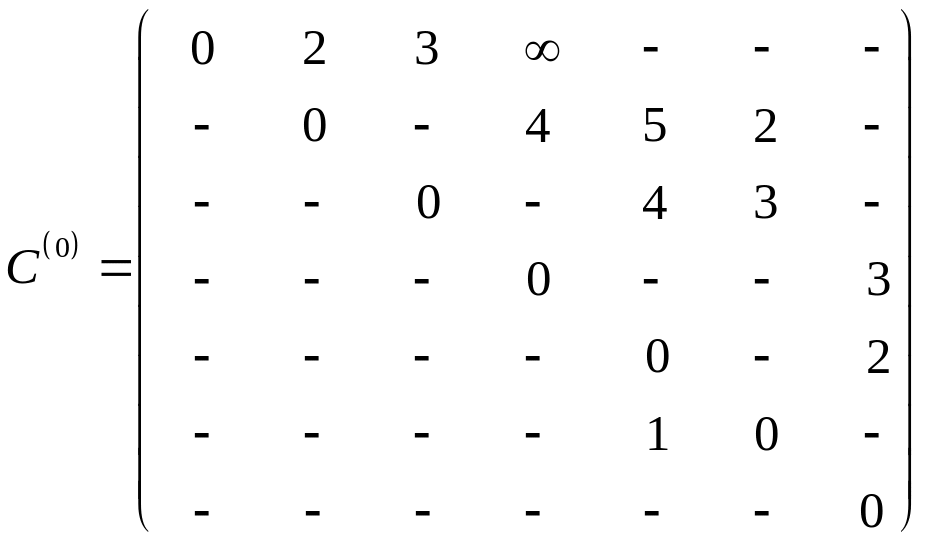– без
изменения,
.
,
,
,
.
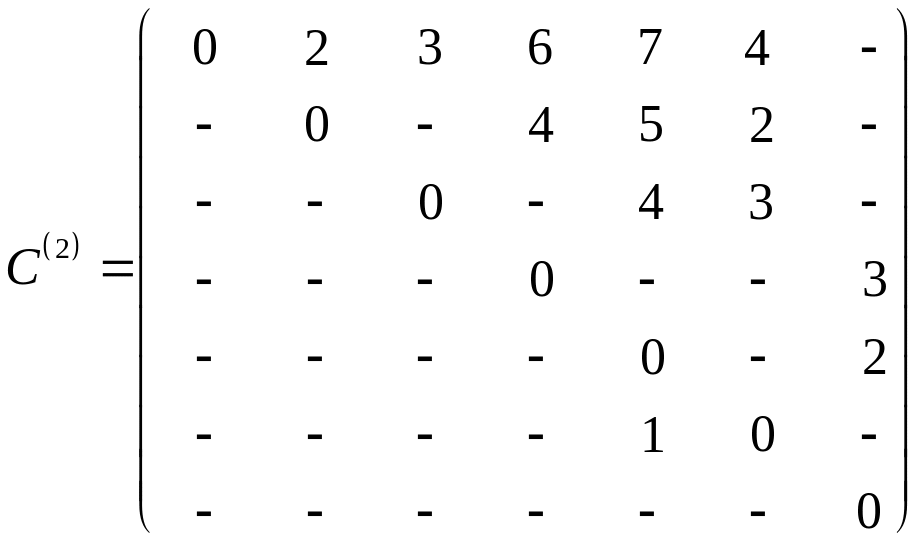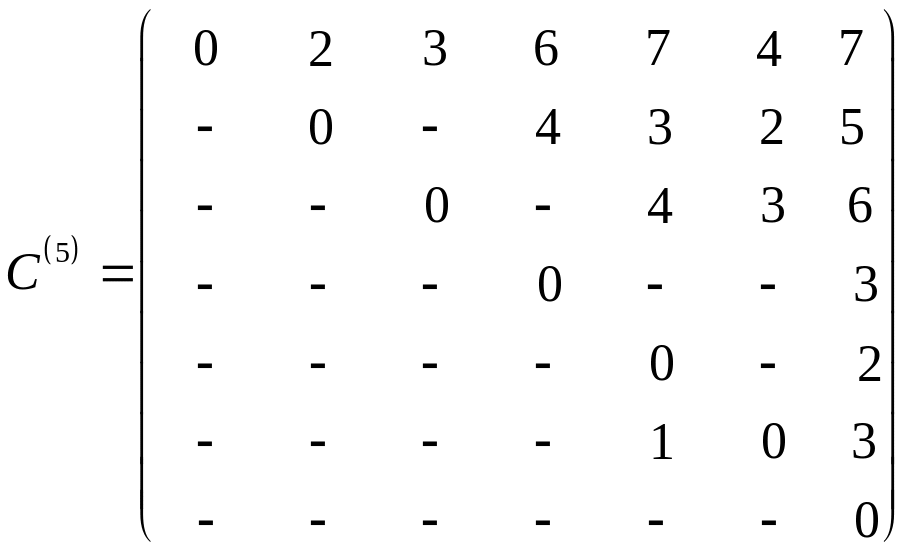– без изменения,
.
,
,
.
,
,
.
,
,
,
.
– без изменения,
.
Так
как
и все
,
то останов. Кратчайшие расстояния между
вершинами
и
получаем из матрицы
.
Например,
,
,
,
и так далее. Сложность алгоритма Флойда
составляет
.