4.2. Остовы. Теорема Кирхгофа

Подграф исходного графа , являющийся деревом и содержащий все его вершины, называется остовом.

Теорема 4.2.1. Граф тогда и только тогда содержит остов, когда он связен.

Доказательство. Если граф не связен, то все его подграфы, у которых множество вершин совпадает с множеством вершин исходного графа, несвязны и не могут содержать дерева.

Обратно. Пусть граф связен. Выясним, имеется ли в нем ребро, удаление которого не нарушает связности. Если таких ребер нет, то граф сам является остовным деревом. Если такое ребро есть, то удалим его и выясним, имеется ли в полученном графе ребро, удаление которого не нарушает связности, и так далее.

Когда удаление ребра без нарушения связности станет невозможным, получим остовное дерево.

Эта теорема дает также алгоритм построения некоторого остовного дерева.

Для подсчета числа остовов графа используется матрица Кирхгофа.

Теорема 4.2.2. [Кирхгоф Г.]. Число остовных деревьев в связном графе порядка равно алгебраическому дополнению любого диагонального элемента матрицы Кирхгофа , где

Подсчитаем, например, число всех остовов графа, изображенного на рис. 4.2.1.

Матрица Кирхгофа этого графа имеет вид:

Минор любого диагонального элемента этой матрицы равен

Следовательно, данный граф имеет 16 остовных деревьев.

Следствие 4.2.1. Число остовов в полном графе равно .

Доказательство. Утверждение очевидно для и . Пусть . Имеем

.

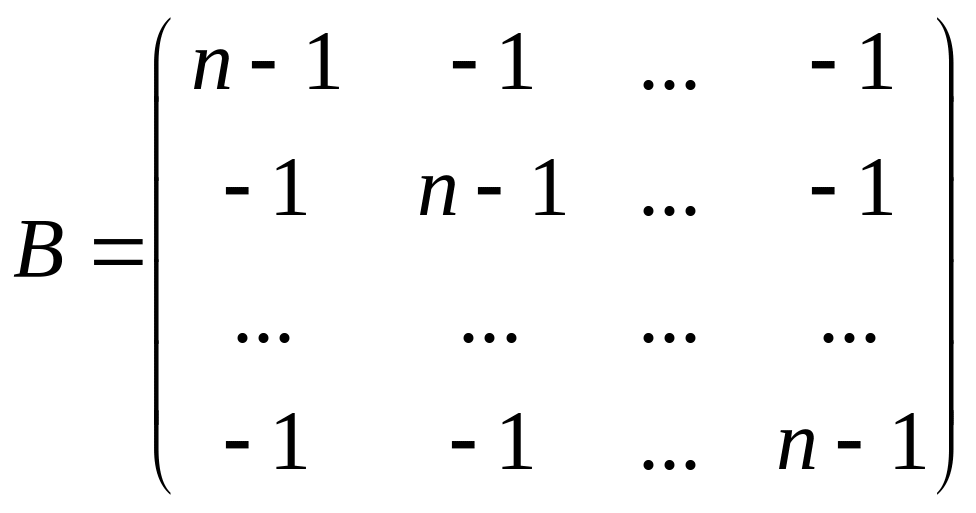Вычислив определитель -го порядка, получаем .

4.3. Теорема Кэли

Обозначим через число помеченных деревьев с вершинами. Ясно, что . Помеченное дерево с тремя вершинами полностью определяется центральной вершиной, поэтому . Дерево с четырьмя вершинами представляет собой либо полный двудольный граф , либо простую (незамкнутую) цепь длины три. 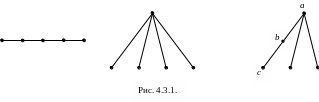Различных помеченных деревьев первого типа имеется четыре, а второго – (крайние вершины цепи выбираются способами, после чего для нумерации двух оставшихся вершин остается возможности); таким образом, Дерево с пятью вершинами имеет один из трех видов, изображенных на рис. 4.3.1.

Количество деревьев типа «цепь» равно типа . Произвольное дерево третьего типа определяется метками вершин и их число равно Итак, Последовательность может быть задана соотношением Число помеченных деревьев с шестью вершинами также нетрудно подсчитать, после чего равенство получит еще одно подтверждение. В общем случае имеет место теорема.

Теорема 4.3.1. [Кэли А., 1897 г.]. Число помеченных деревьев с вершинами равно

Доказательство. Так как число помеченных деревьев порядка n равно числу остовов в полном графе , то теорема эквивалентна следствию 4.2.1.

По формуле подсчитывается число всех деревьев с данными вершинами. Многие из этих деревьев изоморфны. Число неизоморфных деревьев подсчитывается по алгоритму теории Пойа (см., например, [11]).