
- •1. Общие сведения.
- •1.1. Основные понятия и определения.
- •1.2. Переменные в управлениях осу
- •1.3. Управление объектом
- •1.4. Классификация оптимальных систем управления.
- •2. Математическое описание
- •2.1. Уравнения в переменных состояния.
- •2.2. Представление нормальной системы уравнений в матричной форме.
- •2.3. Характеристическое уравнение в матричной форме.
- •2.4. Матричная передаточная функция.
- •2.5. Решение неоднородного матричного уравнения.
- •2.6. Метод фазовой плоскости
- •2.6.1. Особенности нелинейных систем
- •2.6.2. Изображение процессов на фазовой плоскости.
- •2.7. Фазовые портреты линейной системы
- •2.8. Фазовые портреты нелинейной системы.
- •2.9. Пример определения особых точек фазового портрета нелинейной системы.
- •2.10. Управление в фазовом пространстве.
- •Свободное движение.
- •Состояние равновесия.
- •Фазовый портрет при положительном управлении.
- •Фазовый портрет при отрицательном управлении.
- •Изменение движения изображающей точки.
- •3. Оптимальные системы.
- •3.1. Статическая оптимизация
- •Безусловная оптимизация
- •Условная оптимизация.
- •3.2. Динамическая оптимизация.
- •3.3. Функционал и его вариация.
- •3.4. Уравнение Эйлера.
- •3.5. Задачи вариационного исчисления
- •3.6. Принцип максимума.
- •3.7. Оптимальное по быстродействию управление на принципе максимума.
- •4. Адаптивные системы
- •4.1. Основные принципы
- •4.2. Постановка задачи.
- •3.2. Способы поиска экстремума.
- •4.3. Способы поиска экстремума.
2.7. Фазовые портреты линейной системы
Для каждого решения дифференциального уравнения можно построить фазовый портрет, который будет выражать графически движение системы. Решение линейного дифференциального уравнения - это сумма экспонент, степени которых – корни характеристического уравнения. Получается, что вид фазового портрета определятся тем, какие корни будет иметь характеристическое уравнение.
Запишем систему (2.18.) как систему линейных уравнений:
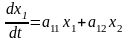 ,
,
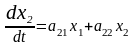 ,
,
где
 -
коэффициенты.
-
коэффициенты.
Составим характеристическую матрицу pE-A :
 .
.
Определитель этой матрицы, приравненный нулю, даёт характеристическое уравнение:
 ,
,
Корни
 этого
уравнения определяют вид особой точки
и, следовательно, вид фазовой траектории.
этого
уравнения определяют вид особой точки
и, следовательно, вид фазовой траектории.
Решение может быть устойчивым и неустойчивым.
Устойчивые решения дают те корни, у которых действительная часть отрицательная:
 и
и
 .
.
Переходной процесс и фазовый портрет для корней показаны на рис 2.8. и рис 2.9.
Переходной процесс – затухающие колебания. Фазовый портрет – скручивающие спирали.

Начало координат на рис. 2.9 называется особой точкой типа “устойчивый фокус”.
На рис. 2.10 и рис. 2.11 показан переходной процесс для корней:

Начало координат на рис. 2.11 называют особой точкой типа “устойчивый узел”.
Если
действительные части комплексных
корней положительные,
 ,
система неустойчивая.
,
система неустойчивая.
Переходной процесс – нарастающие колебания, изображен на рис 2.12. Фазовый портрет – раскручивающиеся спирали, изображен на рис 2.13.

Начало координат на рис 2.13 – особая точка типа “неустойчивый фокус”.
Неустойчивой
система может быть по причине
положительных действительных корней,
 .
Пояснение на рис 2.14
и рис 2.15.
.
Пояснение на рис 2.14
и рис 2.15.
Начало координат на рис 2.15 – особая точка типа “неустойчивый узел”.
Если один из действительных корней отрицательный, а другой – положительный, то система так же будет неустойчивой. На рис 2.16 показан переходной процесс, на рис 2.17 фазовый портрет.

Начало координат на рис 2.17 – особая точка типа “седло”.
Мнимые
корни
 обеспечивают системе незатухающие
колебания с постоянной амплитудой –
гармонические. Им соответствует
фазовый портрет в виде вложенных друг
в друга эллипсов, рис 2.18.
обеспечивают системе незатухающие
колебания с постоянной амплитудой –
гармонические. Им соответствует
фазовый портрет в виде вложенных друг
в друга эллипсов, рис 2.18.

Начало координат носит название особой точки типа “центр”.
Анализ фазовых портретов и особых точек линейной системы, описываемый дифференциальным уравнением второго порядка, показывает следующее:
1. Фазовое пространство линейного дифференциального уравнения содержит только одну точку – начало координат;
2. Фазовые траектории нигде не пересекаются, кроме как в особой точке;
3. Область притяжения особой точки (если система устойчивая) или область отталкивания (если система неустойчивая) охватывает все фазовое пространство;
4. За исключением гармонического движения, фазовое пространство не содержит замкнутых фазовых траекторий.
