14: Элементы трёхпроекционного комплексного чертежа точки.

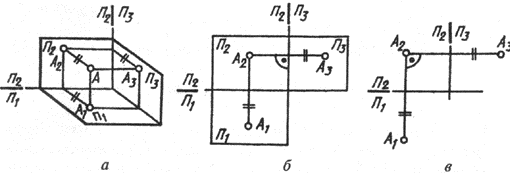Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П₁ и фронтальной плоскости проекций П₂ (рис. 62, а). В результате пересечения фронтальной П₂ и профильной П₃ плоскостей проекций получаем новую ось П₂/П₃, которая располагается на комплексном чертеже параллельно вертикальной линии связи A₁A₂ (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А₂ новой линией связи, которую называют горизонталь ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A₁A₂ _|_ А₂А₁ и А₂А₃, _|_ П₂/П₃.Положение точки в пространстве в этом случае характеризуется ее широтой — расстоянием от нее до профильной плоскости проекций П₃, которое обозначим буквой р.Полученный комплексный чертеж точки называется трехпроекционным. В трехпроекционном чертеже глубина точки АА₂ проецируется без искажений на плоскости П₁и П₂ (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А₁ и фронтальной А₂ проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A₂A₃ _|_A₂A₁. Затем в любом месте на чертеже провести ось проекций П₂/П₃ _|_ А₂А₃, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П₂/П₃. Получим профильную проекцию А₃ точки А.Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции. на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в).

В тех случаях, когда условиями задачи этого не требуется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).

15: Многогранные поверхности. Многогранники.

Многогранная поверхность-поверхность, образовавшая частями попарно пересекающихся плоскостей. Из элементами являются грани, рёбра и вершины. Грани-отсеки плоскостей, образующие многогранную поверхность. Рёбра-линии пересечения смежных граней. Вершины-точки пересечения не менее чем 3 граней. Если каждое ребро многогранной поверхности принадлежит одновременно двум её граням, её называют замкнутой, в противном случае- незамкнутой. Пирамидальная поверхность- если все её рёбра пересекаются в одной точке-вершине. Призматическая поверхность – если все рёбка параллельны между собой. Многогранник- геометрическое тело, со всех сторон ограниченное плоскими многоугольниками. Многогранники-пирамиды и призмы., призматоиды (многоугольники у которых верхнее и нижнее основание - многоугольники расположенные в параллельных плоскостях, а боковые грани представляют собой треугольники или трапеции), правильные многогранники(их п видов: тетраэдр(четырёхгранник)-ограничен 4-мя равносторонними и равными треугольниками; тетраэдр (четырёхугольник или куб)- ограничен 6-ю равными квадратами; октаэдр(восьмигранник)-ограничен 8-ю равносторонними и равными треугольниками; додекаэдр(12-ик)-органичен 12-ю равносторонними и равными пятиугольниками; икосаэдр (20-ик)-органичен 20-ю равными и равностор. Тр-ами.).Вокруг всех прав. Многоуг-ов можно описать сферу.

Совокупность всех рёбер и вершин многогранника называется его сеткой. Построение проекций многогранника сводится к построению проекций его сетки. Количество проекций многогранника должно быть таким, чтоб обеспечить обратимость чертежа. Обратимый чертёж если до одной проекции точки, принадлежащей поверхности, можно построить её 2-ю проекцию. Двухпраекционный чертёж многогранника, состоящий из горизонтальной и фронтальной проекций, является обратимым ,если на нём нет совпадающих проекций рёбер и ни одно ребро не является профильной прямой. Если эти условия не выполняются, то для придания чертежу свойства обратимости нужно построить третью проекцию многогранника или же обозначить все его вершины. Видимость проекций- линии, расположенных внутри очерка, определяется при помощи конкурирующих точек. Существенную помощь при этом могут оказать следующие правила:

1.если внутри очерка пересекается 2 линии, то одна из них видимая, а другая-невидимая.

2.если внутри очерка пересекаются в одной точке 3 линии, то все 3 будут видимые или все 3 невидимые.

3.если последовательность букв или цифр при обходе какой-либо грани в одном направлении одинаковы на обеих проекциях, то и видимость на обеих проекциях одинакова, в противном случае- разная.

При определении видимости проекций многогранника, основания которого параллельны плоскости проекций, рекомендуется пользоваться следующими правилами:

1.линии, образующие внешней контур каждой проекции, всегда видимы.

2.горизонтальные проекции сторон нижнего основания видимы те, которые входят в соответствующие очерки, горизонтальные проекции сторон верхнего основания видимы все.

3.на плоскости П видимы проекции тех граней, которые проходят через видимые на ней проекции сторон нижнего основания.

4.на плоскости П видимы те грани, которые проходят через впереди лежащие стороны нижнего основания.

Если все грани многоугольника расположены по одну сторону плоскости любой его грани то многоугольник называется выпуклым. Для всякого выпуклого многоугольника справедлива теорема Эйлера:Г+В-Р=2…где Г-число граней. В-число вершин. Р- число рёбер.