Реакция заделки.

Р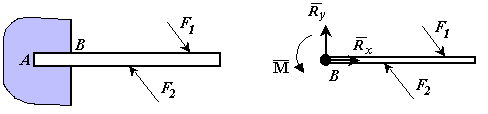 ассмотрим балку один конец которой АВ заделан в стену. Такое крепление конца балки АВ называется заделкой в точке В. Пусть на балку действует плоская система сил. Определим силы, которые надо приложить к точке В балки, если часть балки АВ отбросить. К сечению балки (В) приложены распределенные силы реакции. Если эти силы заменить элементарными сосредоточенными силами и затем привести их к точке В, то в точке В получим силу (главный вектор сил реакции) и пару сил с моментом М (главный вектор сил реакции относительно точки В) . Момент М называют моментом заделки или рективным моментом. Силу реакции можно заменить двумя составляющими и .

Заделка в отличие от шарнира создает не только неизвестную по величине и направлению реакцию , но еще и пару сил с неизвестным моментом М в заделке.

8. Равновесие системы тел. Определение реакций внешних и внутренних связей.

Рассмотрим равновесие сил, приложенных к системе взаимодействующих между собой тел. Тела могут быть соединены между собой с помощью шарниров или иным способом.

Силы, действующие на рассматриваемую систему тел, можно разделить на внешние и внутренние.

Внешними называются силы, с которыми на тела рассматриваемой системы действуют тела, не входящие в эту систему сил.

Внутренними называются силы взаимодействия между телами рассматриваемой системы.

Связи, соединяющие части данной конструкции, будем называть внутренними в отличие от внешних связей, скрепляющих конструкцию с телами, в нее не входящими (например, с опорами).

Способ решения подобных задач состоит в том, что конструкцию сразу расчленяют на отдельные тела и составляют условия равновесия каждого из тел в отдельности (см. задачу 24). При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению. Для конструкции из п тел, на каждое из которых действует произвольная плоская система сил, получится таким путем Зп уравнений, позволяющих найти Зп неизвестных (при других системах сил число уравнений соответственно изменится). Если для данной конструкции число всех реакций связей будет больше числа уравнений, в которые эти реакции входят, то конструкция будет статически неопределимой.

Внутренними усилиями в каком-нибудь сечении тела или конструкции (балки, арки и др.) называют силы, с которыми части тела, разделенные этим сечением, действуют друг на друга. Метод определения внутренних усилий аналогичен методу, применяемому при изучении равновесия систем тел. Сначала рассматривают равновесие всего тела (конструкции) в целом и определяют реакции внешних связей. Затем сечением, в котором требуется найти внутренние усилия, разделяют тело на две части и рассматривают равновесие одной из них. При этом, если система действующих на тело внешних сил плоская, то действие отброшенной части заменится в общем случае' плоской системой распределенных по сечению сил; эти силы, как и в случае жесткой заделки (см. рис. 55), представляют одной приложенной в центре сечения силой с двумя наперед неизвестными, составляющими X, Y и парой с наперед неизвестным моментом m.