1. Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор г, проведенный из начала координат О в точку М.

При движении точки М вектор г будет с течением времени изменяться и по модулю, и по направлению. Следовательно, г является переменным вектором (вектором-функцией), зависящим от аргумента t: r=r(t)

Геометрическое место концов вектора r, т. е. годограф этого вектора, определяет траекторию движущейся точки.

Аналитически, как известно, вектор задается его проекциями на координатные оси.

Следовательно, зависимость г от t будет известна, если будут заданы координаты х, у, z точки как функции времени.

Вектор г может быть задан, как известно, и иными способами, например его модулем и углами с осями или проекциями на оси других систем координат. Для получения общих формул, не зависящих от того, как конкретно задан век гор г, будем исходить из векторного закона движения, представленного равенством.

2. Координатный способ задания движения точки.

Положение точки можно непосредственно определять ее декартовыми координатами х, у, z, которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т. е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени.

, ,

Уравнения движения есть также уравнения траектории точки в параметрической форме. Параметром является время t.

(1-3)

Уравнения траектории в координатной форме получаются из уравнений (1-2) исключением параметра t. Получаются уравнения двух поверхностей , . Пересечение этих поверхностей дает кривую в пространстве – траекторию точки.

1. Естественный способ задания движения точки.

Естественным (или траекторным) способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz. Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси). Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой s, которая равна расстоянию от точки О' до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения Mlt Мг,следовательно, расстояние s будет с течением времени изменяться. Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s=f(t)

- закон движения точки по траектории.

Таким образом, чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки; 2) начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета; 3) закон движения точки вдоль траектории в виде s=f(t)

37. Определение траектории, скорости и ускорения точки при векторном способе задания движения. Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета. Геометрическое место концов вектора r, т. е. годограф этого вектора, определяет траекторию движущейся точки.

Скорость точки при векторном способе задания движения

П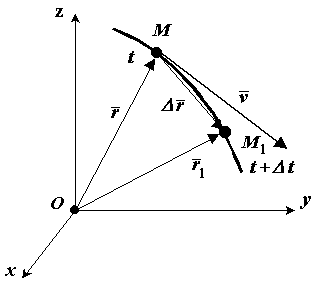 оложение движущейся точки М относительно системы отсчета в момент времени определяется радиус-вектором . В другой момент времени точка займет положение М₁ с радиус-вектором . За время радиус-вектор движущейся точки изменится на .

Средней скоростью называется отношение изменения радиус-вектора к изменению времени .

(1-4)

Скорость точки равна первой производной по времени от ее радиус-вектора.

Средним ускорением точки за время называется отношение вектора приращения скорости к изменению времени .

(2-3)

Ускорением точки в момент времени называется предел к которому стремится среднее ускорение при , стремящемся к нулю. Ускорение точки равно первой производной по времени от скорости точки или второй производной по времени от радиус-вектора.